Calibration of a diffraction setup using Jupyter notebooks
This notebook presents a very simple GUI for doing the calibration of diffraction setup within the Jupyter lab or notebook environment with Matplotlib and Ipywidgets. It has been tested with widget and the notebook (aka nbagg) integration of matplotlib.
Despite this is in the cookbook section, this tutorial requires advanced Python programming knowledge and some good understanding of PyFAI.
This tutorial is also available as a video:
[1]:
#Video of this tutorial
from IPython.display import Video
Video("http://www.silx.org/pub/pyFAI/video/Calibration_Jupyter.mp4", width=800)
[1]:
The basic idea is to port directly the original pyFAI-calib tool which was done with matplotlib into the Jupyter notebooks. Most credits go Philipp Hans for the adaptation of the origin PeakPicker class to Jupyter.
The PeakPicker widget has been refactored and the Calibration tool adapted for the notebook usage. Several external tools were used with the following version:
jupyterlab: 3.2.8
notebook: 6.1.6
matplotlib: 3.5.1
ipympl: 0.8.6
ipywidgets: 7.6.5
[1]:
%matplotlib nbagg
# The notebook interface (nbagg) is needed in jupyter-notebook while the widget is recommended for jupyer lab
# %matplotlib widget
import pyFAI
import pyFAI.test.utilstest
import fabio
from matplotlib.pyplot import subplots
from pyFAI.gui import jupyter
from pyFAI.gui.jupyter.calib import Calibration
print(f"PyFAI version {pyFAI.version}")
WARNING:pyFAI.gui.matplotlib:matplotlib already loaded, setting its backend may not work
PyFAI version 0.21.0-dev3
[2]:
# Some parameters like the wavelength, the calibrant and the diffraction image:
wavelength = 1e-10
pilatus = pyFAI.detector_factory("Pilatus1M")
AgBh = pyFAI.calibrant.CALIBRANT_FACTORY("AgBh")
AgBh.wavelength = wavelength
#load some test data (requires an internet connection)
img = fabio.open(pyFAI.test.utilstest.UtilsTest.getimage("Pilatus1M.edf")).data
[3]:
# Simply display the scattering image:
_ = jupyter.display(img)
[4]:
calib = Calibration(img, calibrant=AgBh, wavelength=wavelength, detector=pilatus)
# This displays the calibration widget:
# 1. Set the ring number (0-based value), below the plot
# 2. Pick the ring by right-clicking with the mouse on the image.
# 3. Restart at 1. for at least a second ring
# 4. Click refine to launch the calibration.
Before refinement, the geometry is:
Detector Pilatus 1M PixelSize= 1.720e-04, 1.720e-04 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.000000e-01m PONI= 0.000000e+00, 0.000000e+00m rot1=0.000000 rot2= 0.000000 rot3= 0.000000 rad
DirectBeamDist= 100.000mm Center: x=0.000, y=0.000 pix Tilt=0.000 deg tiltPlanRotation= 0.000 deg
Detector Pilatus 1M PixelSize= 1.720e-04, 1.720e-04 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.633043e+00m PONI= 1.223095e-01, 2.628343e-02m rot1=-0.002844 rot2= -0.047012 rot3= 0.000000 rad
DirectBeamDist= 1634.856mm Center: x=179.817, y=264.421 pix Tilt=2.698 deg tiltPlanRotation= -86.540 deg
Detector Pilatus 1M PixelSize= 1.720e-04, 1.720e-04 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.632826e+00m PONI= 1.222996e-01, 2.628170e-02m rot1=-0.002852 rot2= -0.047013 rot3= 0.000000 rad
DirectBeamDist= 1634.639mm Center: x=179.872, y=264.410 pix Tilt=2.699 deg tiltPlanRotation= -86.531 deg
Detector Pilatus 1M PixelSize= 1.720e-04, 1.720e-04 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.632826e+00m PONI= 1.222996e-01, 2.628170e-02m rot1=-0.002852 rot2= -0.047013 rot3= 0.000000 rad
DirectBeamDist= 1634.639mm Center: x=179.872, y=264.410 pix Tilt=2.699 deg tiltPlanRotation= -86.531 deg
[5]:
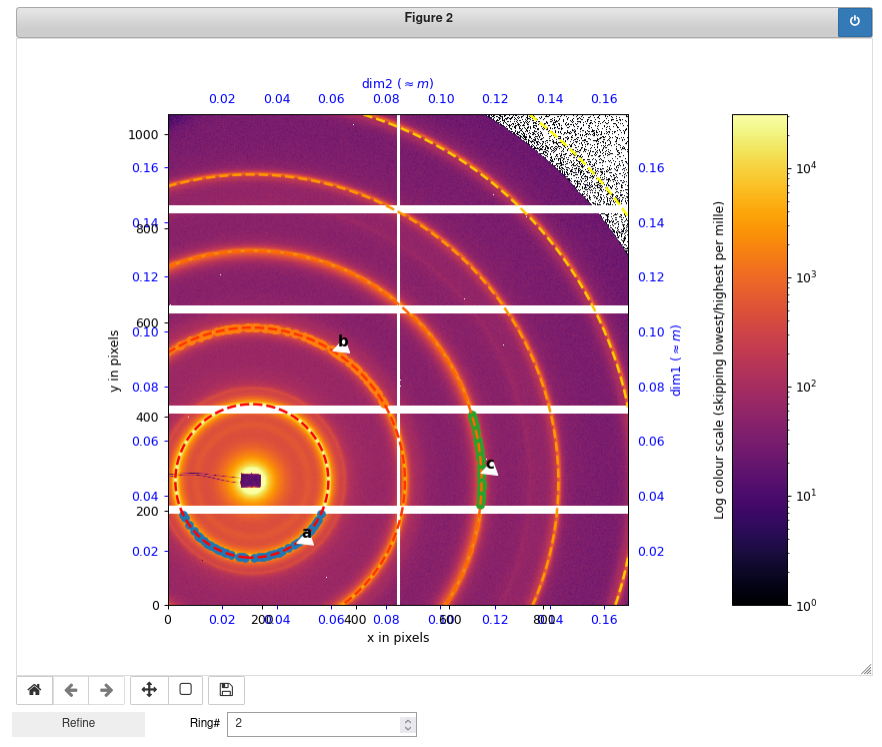
# Here is a screenshot of the previous widget, since it is not recoreded inside the notebook itself.
from IPython.display import Image
Image(filename='pyFAI-calib_notebook.png')
[5]:
[5]:
# This is the calibrated geometry:
gr = calib.geoRef
print(gr)
print(f"Fixed parameters: {calib.fixed}")
print(f"Cost function: {gr.chi2()}")
Detector Pilatus 1M PixelSize= 1.720e-04, 1.720e-04 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.632826e+00m PONI= 1.222996e-01, 2.628170e-02m rot1=-0.002852 rot2= -0.047013 rot3= 0.000000 rad
DirectBeamDist= 1634.639mm Center: x=179.872, y=264.410 pix Tilt=2.699 deg tiltPlanRotation= -86.531 deg
Fixed parameters: ['wavelength', 'rot3']
Cost function: 1.532467318765197e-07
[6]:
# Geometry refinement with some constrains: SAXS mode
# Here we enforce all rotation to be null and fit again the model:
gr.rot1 = gr.rot2 = gr.rot3 = 0
gr.refine3(fix=["rot1", "rot2", "rot3", "wavelength"])
print(gr)
print(f"Cost function = {gr.chi2()}")
Detector Pilatus 1M PixelSize= 1.720e-04, 1.720e-04 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.634831e+00m PONI= 4.543425e-02, 3.093027e-02m rot1=0.000000 rot2= 0.000000 rot3= 0.000000 rad
DirectBeamDist= 1634.831mm Center: x=179.827, y=264.153 pix Tilt=0.000 deg tiltPlanRotation= 0.000 deg
Cost function = 1.5907780154943566e-07
[7]:
gr.save("jupyter.poni")
gr.get_config()
[7]:
OrderedDict([('poni_version', 2),
('detector', 'Pilatus1M'),
('detector_config', OrderedDict()),
('dist', 1.634831396919371),
('poni1', 0.04543425362516216),
('poni2', 0.030930268602695623),
('rot1', 0.0),
('rot2', 0.0),
('rot3', 0.0),
('wavelength', 1e-10)])
[8]:
# Create a "normal" azimuthal integrator (without fitting capabilities from the geometry-refinement object)
ai = pyFAI.load(gr)
ai
[8]:
Detector Pilatus 1M PixelSize= 1.720e-04, 1.720e-04 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.634831e+00m PONI= 4.543425e-02, 3.093027e-02m rot1=0.000000 rot2= 0.000000 rot3= 0.000000 rad
DirectBeamDist= 1634.831mm Center: x=179.827, y=264.153 pix Tilt=0.000 deg tiltPlanRotation= 0.000 deg
[9]:
# Display the integrated data to validate the calibration.
fig, ax = subplots(1, 2, figsize=(10, 5))
jupyter.plot1d(ai.integrate1d(img, 1000), calibrant=AgBh, ax=ax[0])
jupyter.plot2d(ai.integrate2d(img, 1000), calibrant=AgBh, ax=ax[1])
_ = ax[1].set_title("2D integration")
Conclusion
This short notebook shows how to interact with a calibration image to pick some control-point from the Debye-Scherrer ring and to perform the calibration of the experimental setup.