Digital Signatures¶
You can use a digital signature for many of the same reasons that you might sign a paper document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender such that they cannot deny sending it (authentication and non-repudiation) and that the message was not altered in transit (integrity).
Digital signatures allow you to publish a public key, and then you can use your private signing key to sign messages. Others who have your public key can then use it to validate that your messages are actually authentic.
Example¶
Signing and verifying a message without encoding the key or message
Signer’s perspective (SigningKey)
from nacl.signing import SigningKey
# Generate a new random signing key
signing_key = SigningKey.generate()
# Sign a message with the signing key
signed = signing_key.sign(b"Attack at Dawn")
# Obtain the verify key for a given signing key
verify_key = signing_key.verify_key
# Serialize the verify key to send it to a third party
verify_key_bytes = verify_key.encode()
Verifier’s perspective (VerifyKey)
from nacl.signing import VerifyKey
# Create a VerifyKey object from a hex serialized public key
verify_key = VerifyKey(verify_key_bytes)
# Check the validity of a message's signature
# The message and the signature can either be passed together, or
# separately if the signature is decoded to raw bytes.
# These are equivalent:
verify_key.verify(signed)
verify_key.verify(signed.message, signed.signature)
# Alter the signed message text
forged = signed[:-1] + bytes([int(signed[-1]) ^ 1])
# Will raise nacl.exceptions.BadSignatureError, since the signature check
# is failing
verify_key.verify(forged)
Traceback (most recent call last):
...
nacl.exceptions.BadSignatureError: Signature was forged or corrupt
Example¶
Signing and verifying a message encoded with HexEncoder
Signer’s perspective (SigningKey)
from nacl.encoding import HexEncoder
from nacl.signing import SigningKey
# Generate a new random signing key
signing_key = SigningKey.generate()
# Sign a message with the signing key
signed_hex = signing_key.sign(b"Attack at Dawn", encoder=HexEncoder)
# Obtain the verify key for a given signing key
verify_key = signing_key.verify_key
# Serialize the verify key to send it to a third party
verify_key_hex = verify_key.encode(encoder=HexEncoder)
Verifier’s perspective (VerifyKey)
from nacl.encoding import HexEncoder
from nacl.signing import VerifyKey
# Create a VerifyKey object from a hex serialized public key
verify_key = VerifyKey(verify_key_hex, encoder=HexEncoder)
# Check the validity of a message's signature
# The message and the signature can either be passed together, or
# separately if the signature is decoded to raw bytes.
# These are equivalent:
verify_key.verify(signed_hex, encoder=HexEncoder)
signature_bytes = HexEncoder.decode(signed_hex.signature)
verify_key.verify(signed_hex.message, signature_bytes,
encoder=HexEncoder)
# Alter the signed message text
forged = signed_hex[:-1] + bytes([int(signed_hex[-1]) ^ 1])
# Will raise nacl.exceptions.BadSignatureError, since the signature check
# is failing
verify_key.verify(forged)
Traceback (most recent call last):
...
nacl.exceptions.BadSignatureError: Signature was forged or corrupt
Example¶
Signing and verifying a message encoded with Base64Encoder
Signer’s perspective (SigningKey)
from nacl.encoding import Base64Encoder
from nacl.signing import SigningKey
# Generate a new random signing key
signing_key = SigningKey.generate()
# Sign a message with the signing key
signed_b64 = signing_key.sign(b"Attack at Dawn", encoder=Base64Encoder)
# Obtain the verify key for a given signing key
verify_key = signing_key.verify_key
# Serialize the verify key to send it to a third party
verify_key_b64 = verify_key.encode(encoder=Base64Encoder)
Verifier’s perspective (VerifyKey)
from nacl.encoding import Base64Encoder
from nacl.signing import VerifyKey
# Create a VerifyKey object from a base64 serialized public key
verify_key = VerifyKey(verify_key_b64, encoder=Base64Encoder)
# Check the validity of a message's signature
# The message and the signature can either be passed together, or
# separately if the signature is decoded to raw bytes.
# These are equivalent:
verify_key.verify(signed_b64, encoder=Base64Encoder)
signature_bytes = Base64Encoder.decode(signed_b64.signature)
verify_key.verify(signed_b64.message, signature_bytes,
encoder=Base64Encoder)
# Alter the signed message text
forged = signed_b64[:-1] + bytes([int(signed_b64[-1]) ^ 1])
# Will raise nacl.exceptions.BadSignatureError, since the signature check
# is failing
verify_key.verify(forged)
Traceback (most recent call last):
...
nacl.exceptions.BadSignatureError: Signature was forged or corrupt
Reference¶
- class nacl.signing.SigningKey(seed, encoder)[source]¶
Private key for producing digital signatures using the Ed25519 algorithm.
Signing keys are produced from a 32-byte (256-bit) random seed value. This value can be passed into the
SigningKeyas abytes()whose length is 32.Warning
This must be protected and remain secret. Anyone who knows the value of your
SigningKeyor its seed can masquerade as you.- Parameters
seed (bytes) – Random 32-byte value (i.e. private key).
encoder – A class that is able to decode the
seed.
- classmethod generate()[source]¶
Generates a random
SigningKeyobject- Returns
An instance of
SigningKey.
- sign(message, encoder)[source]¶
Sign a message using this key.
- Parameters
message (bytes) – The data to be signed.
encoder – A class that is able to decode the signed message.
- Returns
An instance of
SignedMessage.
- class nacl.signing.VerifyKey(key, encoder)[source]¶
The public key counterpart to an Ed25519
SigningKeyfor producing digital signatures.- Parameters
key (bytes) – A serialized Ed25519 public key.
encoder – A class that is able to decode the
key.
- verify(smessage, signature, encoder)[source]¶
Verifies the signature of a signed message.
- Parameters
smessage (bytes) – The signed message to verify. This is either the original message or the concatenated signature and message.
signature (bytes) – The signature of the message to verify against. If the value of
smessageis the concatenated signature and message, this parameter can beNone.encoder – A class that is able to decode the secret message and signature.
- Return bytes
The message if successfully verified.
- Raises
nacl.exceptions.BadSignatureError – This is raised if the signature is invalid.
- class nacl.signing.SignedMessage[source]¶
A bytes subclass that holds a messaged that has been signed by a
SigningKey.- signature¶
The signature contained within the
SignedMessage.
- message¶
The message contained within the
SignedMessage.
Ed25519¶
Ed25519 is a public-key signature system with several attractive features:
Fast single-signature verification: Ed25519 takes only 273364 cycles to verify a signature on Intel’s widely deployed Nehalem/Westmere lines of CPUs. (This performance measurement is for short messages; for very long messages, verification time is dominated by hashing time.) Nehalem and Westmere include all Core i7, i5, and i3 CPUs released between 2008 and 2010, and most Xeon CPUs released in the same period.
Even faster batch verification: Ed25519 performs a batch of 64 separate signature verifications (verifying 64 signatures of 64 messages under 64 public keys) in only 8.55 million cycles, i.e., under 134000 cycles per signature. Ed25519 fits easily into L1 cache, so contention between cores is negligible: a quad-core 2.4GHz Westmere verifies 71000 signatures per second, while keeping the maximum verification latency below 4 milliseconds.
Very fast signing: Ed25519 takes only 87548 cycles to sign a message. A quad-core 2.4GHz Westmere signs 109000 messages per second.
Fast key generation: Key generation is almost as fast as signing. There is a slight penalty for key generation to obtain a secure random number from the operating system; /dev/urandom under Linux costs about 6000 cycles.
High security level: This system has a 2^128 security target; breaking it has similar difficulty to breaking NIST P-256, RSA with ~3000-bit keys, strong 128-bit block ciphers, etc. The best attacks known actually cost more than 2^140 bit operations on average, and degrade quadratically in success probability as the number of bit operations drops.
Collision resilience: Hash-function collisions do not break this system. This adds a layer of defense against the possibility of weakness in the selected hash function.
No secret array indices: Ed25519 never reads or writes data from secret addresses in RAM; the pattern of addresses is completely predictable. Ed25519 is therefore immune to cache-timing attacks, hyperthreading attacks, and other side-channel attacks that rely on leakage of addresses through the CPU cache.
No secret branch conditions: Ed25519 never performs conditional branches based on secret data; the pattern of jumps is completely predictable. Ed25519 is therefore immune to side-channel attacks that rely on leakage of information through the branch-prediction unit.
Small signatures: Ed25519 signatures are only 512-bits (64 bytes), one of the smallest signature sizes available.
Small keys: Ed25519 keys are only 256-bits (32 bytes), making them small enough to easily copy and paste. Ed25519 also allows the public key to be derived from the private key, meaning that it doesn’t need to be included in a serialized private key in cases you want both.
Deterministic: Unlike (EC)DSA, Ed25519 does not rely on an entropy source when signing messages (which has lead to catastrophic private key compromises), but instead computes signature nonces from a combination of a hash of the signing key’s “seed” and the message to be signed. This avoids using an entropy source for nonces, which can be a potential attack vector if the entropy source is not generating good random numbers. Even a single reused nonce can lead to a complete disclosure of the private key in these schemes, which Ed25519 avoids entirely by being deterministic instead of tied to an entropy source.
The numbers 87548 and 273364 shown above are official eBATS reports for a Westmere CPU (Intel Xeon E5620, hydra2).
Ed25519 signatures are elliptic-curve signatures, carefully engineered at several levels of design and implementation to achieve very high speeds without compromising security.
Algorithm¶
Signatures: Ed25519 digital signature system
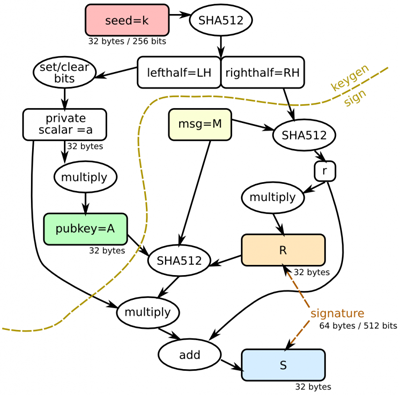
- k
Ed25519 private key (passed into
SigningKey)- A
Ed25519 public key derived from k
- M
message to be signed
- R
a deterministic nonce value calculated from a combination of private key data RH and the message M
- S
Ed25519 signature