Convolution and Filtering (astropy.convolution)

Introduction

astropy.convolution provides convolution functions and kernels that offer improvements compared to the SciPy scipy.ndimage convolution routines, including:

  • Proper treatment of NaN values (ignoring them during convolution and replacing NaN pixels with interpolated values)

  • A single function for 1D, 2D, and 3D convolution

  • Improved options for the treatment of edges

  • Both direct and Fast Fourier Transform (FFT) versions

  • Built-in kernels that are commonly used in Astronomy

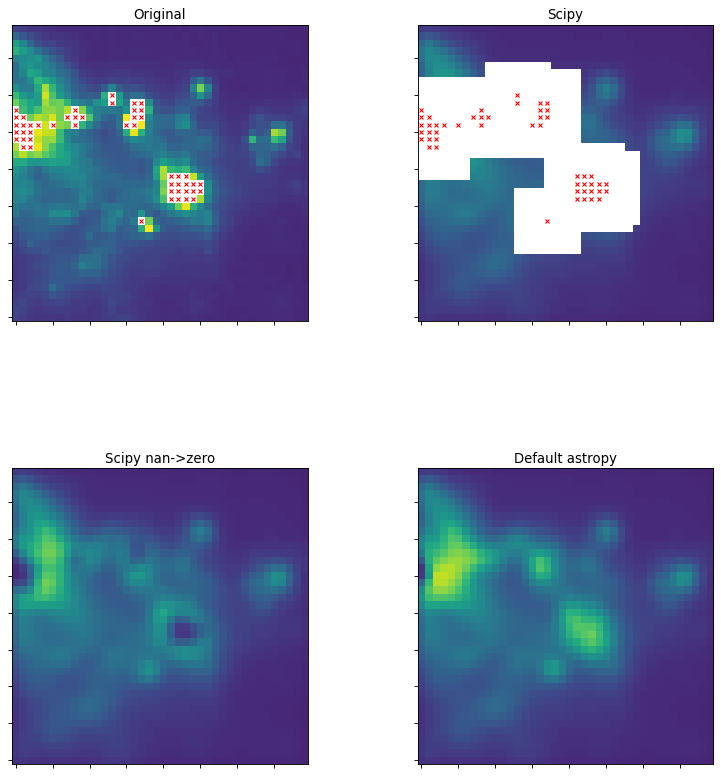
The following thumbnails show the difference between scipy and astropy convolve functions on an astronomical image that contains NaN values. scipy’s function essentially returns NaN for all pixels that are within a kernel of any NaN value, which is often not the desired result.

import numpy as np
import matplotlib.pyplot as plt

from astropy.io import fits
from astropy.utils.data import get_pkg_data_filename
from astropy.convolution import Gaussian2DKernel
from scipy.signal import convolve as scipy_convolve
from astropy.convolution import convolve


# Load the data from data.astropy.org
filename = get_pkg_data_filename('galactic_center/gc_msx_e.fits')
hdu = fits.open(filename)[0]

# Scale the file to have reasonable numbers
# (this is mostly so that colorbars do not have too many digits)
# Also, we crop it so you can see individual pixels
img = hdu.data[50:90, 60:100] * 1e5

# This example is intended to demonstrate how astropy.convolve and
# scipy.convolve handle missing data, so we start by setting the
# brightest pixels to NaN to simulate a "saturated" data set
img[img > 2e1] = np.nan

# We also create a copy of the data and set those NaNs to zero.  We will
# use this for the scipy convolution
img_zerod = img.copy()
img_zerod[np.isnan(img)] = 0

# We smooth with a Gaussian kernel with x_stddev=1 (and y_stddev=1)
# It is a 9x9 array
kernel = Gaussian2DKernel(x_stddev=1)

# Convolution: scipy's direct convolution mode spreads out NaNs (see
# panel 2 below)
scipy_conv = scipy_convolve(img, kernel, mode='same', method='direct')

# scipy's direct convolution mode run on the 'zero'd' image will not
# have NaNs, but will have some very low value zones where the NaNs were
# (see panel 3 below)
scipy_conv_zerod = scipy_convolve(img_zerod, kernel, mode='same',
                                  method='direct')

# astropy's convolution replaces the NaN pixels with a kernel-weighted
# interpolation from their neighbors
astropy_conv = convolve(img, kernel)


# Now we do a bunch of plots.  In the first two plots, the originally masked
# values are marked with red X's
plt.figure(1, figsize=(12, 12)).clf()
ax1 = plt.subplot(2, 2, 1)
im = ax1.imshow(img, vmin=-2., vmax=2.e1, origin='lower',
                interpolation='nearest', cmap='viridis')
y, x = np.where(np.isnan(img))
ax1.set_autoscale_on(False)
ax1.plot(x, y, 'rx', markersize=4)
ax1.set_title("Original")
ax1.set_xticklabels([])
ax1.set_yticklabels([])

ax2 = plt.subplot(2, 2, 2)
im = ax2.imshow(scipy_conv, vmin=-2., vmax=2.e1, origin='lower',
                interpolation='nearest', cmap='viridis')
ax2.set_autoscale_on(False)
ax2.plot(x, y, 'rx', markersize=4)
ax2.set_title("Scipy")
ax2.set_xticklabels([])
ax2.set_yticklabels([])

ax3 = plt.subplot(2, 2, 3)
im = ax3.imshow(scipy_conv_zerod, vmin=-2., vmax=2.e1, origin='lower',
                interpolation='nearest', cmap='viridis')
ax3.set_title("Scipy nan->zero")
ax3.set_xticklabels([])
ax3.set_yticklabels([])

ax4 = plt.subplot(2, 2, 4)
im = ax4.imshow(astropy_conv, vmin=-2., vmax=2.e1, origin='lower',
                interpolation='nearest', cmap='viridis')
ax4.set_title("Default astropy")
ax4.set_xticklabels([])
ax4.set_yticklabels([])

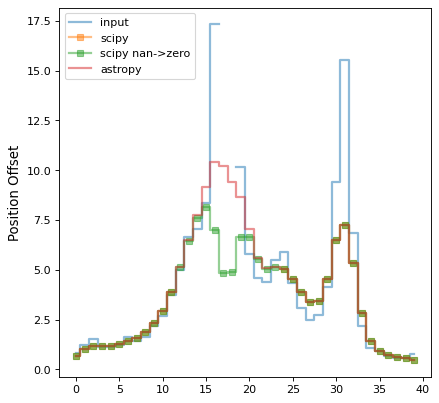
# we make a second plot of the amplitudes vs offset position to more
# clearly illustrate the value differences
plt.figure(2).clf()
plt.plot(img[:, 25], label='input', drawstyle='steps-mid', linewidth=2,
         alpha=0.5)
plt.plot(scipy_conv[:, 25], label='scipy', drawstyle='steps-mid',
         linewidth=2, alpha=0.5, marker='s')
plt.plot(scipy_conv_zerod[:, 25], label='scipy nan->zero',
         drawstyle='steps-mid', linewidth=2, alpha=0.5, marker='s')
plt.plot(astropy_conv[:, 25], label='astropy', drawstyle='steps-mid',
         linewidth=2, alpha=0.5)
plt.ylabel("Amplitude")
plt.ylabel("Position Offset")
plt.legend(loc='best')
plt.show()
../_images/index-1_00.png

(png, svg, pdf)

../_images/index-1_01.png

(png, svg, pdf)

The following sections describe how to make use of the convolution functions, and how to use built-in convolution kernels:

Getting Started

Two convolution functions are provided. They are imported as:

from astropy.convolution import convolve, convolve_fft

and are both used as:

result = convolve(image, kernel)
result = convolve_fft(image, kernel)

convolve() is implemented as a direct convolution algorithm, while convolve_fft() uses a Fast Fourier Transform (FFT). Thus, the former is better for small kernels, while the latter is much more efficient for larger kernels.

Example

To convolve a 1D dataset with a user-specified kernel, you can do:

>>> from astropy.convolution import convolve
>>> convolve([1, 4, 5, 6, 5, 7, 8], [0.2, 0.6, 0.2])  
array([1.4, 3.6, 5. , 5.6, 5.6, 6.8, 6.2])

Notice that the end points are set to zero — by default, points that are too close to the boundary to have a convolved value calculated are set to zero. However, the convolve() function allows for a boundary argument that can be used to specify alternate behaviors. For example, setting boundary='extend' causes values near the edges to be computed, assuming the original data is simply extended using a constant extrapolation beyond the boundary:

>>> from astropy.convolution import convolve
>>> convolve([1, 4, 5, 6, 5, 7, 8], [0.2, 0.6, 0.2], boundary='extend')  
array([1.6, 3.6, 5. , 5.6, 5.6, 6.8, 7.8])

The values at the end are computed assuming that any value below the first point is 1, and any value above the last point is 8. For a more detailed discussion of boundary treatment, see Using the Convolution Functions.

Example

The convolution module also includes built-in kernels that can be imported as, for example:

>>> from astropy.convolution import Gaussian1DKernel

To use a kernel, first create a specific instance of the kernel:

>>> gauss = Gaussian1DKernel(stddev=2)

gauss is not an array, but a kernel object. The underlying array can be retrieved with:

>>> gauss.array  
array([6.69162896e-05, 4.36349021e-04, 2.21596317e-03, 8.76430436e-03,
       2.69959580e-02, 6.47599366e-02, 1.20987490e-01, 1.76035759e-01,
       1.99474648e-01, 1.76035759e-01, 1.20987490e-01, 6.47599366e-02,
       2.69959580e-02, 8.76430436e-03, 2.21596317e-03, 4.36349021e-04,
       6.69162896e-05])

The kernel can then be used directly when calling convolve():

import numpy as np
import matplotlib.pyplot as plt

from astropy.convolution import Gaussian1DKernel, convolve

plt.figure(3).clf()

# Generate fake data
rng = np.random.default_rng(963)
x = np.arange(1000).astype(float)
y = np.sin(x / 100.) + rng.normal(0., 1., x.shape)
y[::3] = np.nan

# Create kernel
g = Gaussian1DKernel(stddev=50)

# Convolve data
z = convolve(y, g)

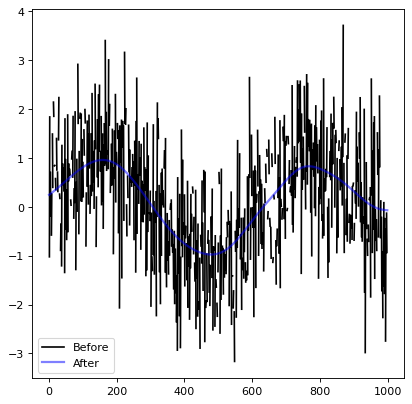
# Plot data before and after convolution
plt.plot(x, y, 'k-', label='Before')
plt.plot(x, z, 'b-', label='After', alpha=0.5, linewidth=2)
plt.legend(loc='best')
plt.show()

(png, svg, pdf)

../_images/index-2.png

Using astropy’s Convolution to Replace Bad Data

astropy’s convolution methods can be used to replace bad data with values interpolated from their neighbors. Kernel-based interpolation is useful for handling images with a few bad pixels or for interpolating sparsely sampled images.

The interpolation tool is implemented and used as:

from astropy.convolution import interpolate_replace_nans
result = interpolate_replace_nans(image, kernel)

Some contexts in which you might want to use kernel-based interpolation include:

  • Images with saturated pixels. Generally, these are the highest-intensity regions in the imaged area, and the interpolated values are not reliable, but this can be useful for display purposes.

  • Images with flagged pixels (e.g., a few small regions affected by cosmic rays or other spurious signals that require those pixels to be flagged out). If the affected region is small enough, the resulting interpolation will have a small effect on source statistics and may allow for robust source-finding algorithms to be run on the resulting data.

  • Sparsely sampled images such as those constructed with single-pixel detectors. Such images will only have a few discrete points sampled across the imaged area, but an approximation of the extended sky emission can still be constructed.

Note

Care must be taken to ensure that the kernel is large enough to completely cover potential contiguous regions of NaN values. An AstropyUserWarning is raised if NaN values are detected post- convolution, in which case the kernel size should be increased.

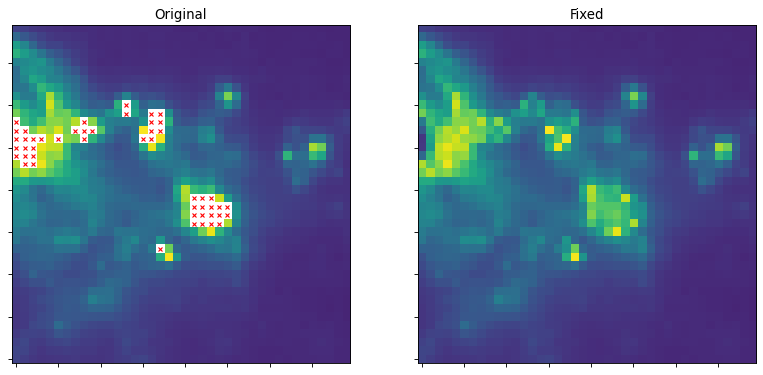
Example

The script below shows an example of kernel interpolation to fill in flagged-out pixels:

import numpy as np
import matplotlib.pyplot as plt

from astropy.io import fits
from astropy.utils.data import get_pkg_data_filename
from astropy.convolution import Gaussian2DKernel, interpolate_replace_nans

# Load the data from data.astropy.org
filename = get_pkg_data_filename('galactic_center/gc_msx_e.fits')

hdu = fits.open(filename)[0]
img = hdu.data[50:90, 60:100] * 1e5

# This example is intended to demonstrate how astropy.convolve and
# scipy.convolve handle missing data, so we start by setting the brightest
# pixels to NaN to simulate a "saturated" data set
img[img > 2e1] = np.nan

# We smooth with a Gaussian kernel with x_stddev=1 (and y_stddev=1)
# It is a 9x9 array
kernel = Gaussian2DKernel(x_stddev=1)

# create a "fixed" image with NaNs replaced by interpolated values
fixed_image = interpolate_replace_nans(img, kernel)

# Now we do a bunch of plots.  In the first two plots, the originally masked
# values are marked with red X's
plt.figure(1, figsize=(12, 6)).clf()
plt.close(2) # close the second plot from above

ax1 = plt.subplot(1, 2, 1)
im = ax1.imshow(img, vmin=-2., vmax=2.e1, origin='lower',
                interpolation='nearest', cmap='viridis')
y, x = np.where(np.isnan(img))
ax1.set_autoscale_on(False)
ax1.plot(x, y, 'rx', markersize=4)
ax1.set_title("Original")
ax1.set_xticklabels([])
ax1.set_yticklabels([])

ax2 = plt.subplot(1, 2, 2)
im = ax2.imshow(fixed_image, vmin=-2., vmax=2.e1, origin='lower',
                interpolation='nearest', cmap='viridis')
ax2.set_title("Fixed")
ax2.set_xticklabels([])
ax2.set_yticklabels([])

(png, svg, pdf)

../_images/index-3.png

Example

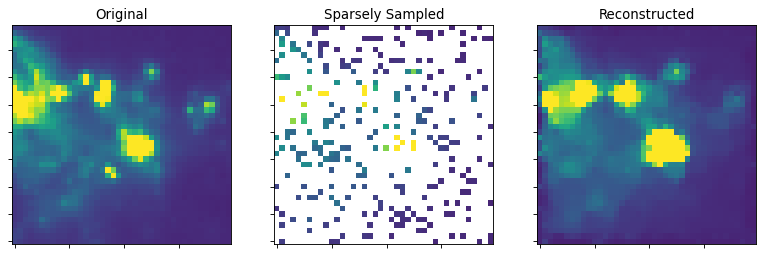
This script shows the power of this technique for reconstructing images from sparse sampling. Note that the image is not perfect: the pointlike sources are sometimes missed, but the extended structure is very well recovered by eye.

import numpy as np
import matplotlib.pyplot as plt

from astropy.io import fits
from astropy.utils.data import get_pkg_data_filename
from astropy.convolution import Gaussian2DKernel, interpolate_replace_nans

# Load the data from data.astropy.org
filename = get_pkg_data_filename('galactic_center/gc_msx_e.fits')

hdu = fits.open(filename)[0]
img = hdu.data[50:90, 60:100] * 1e5

rng = np.random.default_rng(1379)
indices = rng.integers(low=0, high=img.size, size=300)

sampled_data = img.flat[indices]

# Build a new, sparsely sampled version of the original image
new_img = np.tile(np.nan, img.shape)
new_img.flat[indices] = sampled_data

# We smooth with a Gaussian kernel with x_stddev=1 (and y_stddev=1)
# It is a 9x9 array
kernel = Gaussian2DKernel(x_stddev=1)

# create a "reconstructed" image with NaNs replaced by interpolated values
reconstructed_image = interpolate_replace_nans(new_img, kernel)

# Now we do a bunch of plots.  In the first two plots, the originally masked
# values are marked with red X's
plt.figure(1, figsize=(12, 6)).clf()
ax1 = plt.subplot(1, 3, 1)
im = ax1.imshow(img, vmin=-2., vmax=2.e1, origin='lower',
                interpolation='nearest', cmap='viridis')
y, x = np.where(np.isnan(img))
ax1.set_autoscale_on(False)
ax1.set_title("Original")
ax1.set_xticklabels([])
ax1.set_yticklabels([])

ax2 = plt.subplot(1, 3, 2)
im = ax2.imshow(new_img, vmin=-2., vmax=2.e1, origin='lower',
                interpolation='nearest', cmap='viridis')
ax2.set_title("Sparsely Sampled")
ax2.set_xticklabels([])
ax2.set_yticklabels([])

ax2 = plt.subplot(1, 3, 3)
im = ax2.imshow(reconstructed_image, vmin=-2., vmax=2.e1, origin='lower',
                interpolation='nearest', cmap='viridis')
ax2.set_title("Reconstructed")
ax2.set_xticklabels([])
ax2.set_yticklabels([])

(png, svg, pdf)

../_images/index-4.png

Using astropy.convolution

Performance Tips

The convolve() function is best suited to small kernels, and can become very slow for larger kernels. In this case, consider using convolve_fft() (though note that this function uses more memory, and consider the different padding options).

Reference/API

astropy.convolution Package

Functions

convolve(array, kernel[, boundary, ...])

Convolve an array with a kernel.

convolve_fft(array, kernel[, boundary, ...])

Convolve an ndarray with an nd-kernel.

convolve_models(model, kernel[, mode])

Convolve two models using convolve_fft.

convolve_models_fft(model, kernel, ...[, cache])

Convolve two models using convolve_fft.

discretize_model(model, x_range[, y_range, ...])

Function to evaluate analytical model functions on a grid.

interpolate_replace_nans(array, kernel[, ...])

Given a data set containing NaNs, replace the NaNs by interpolating from neighboring data points with a given kernel.

kernel_arithmetics(kernel, value, operation)

Add, subtract or multiply two kernels.

Classes

AiryDisk2DKernel(radius, **kwargs)

2D Airy disk kernel.

Box1DKernel(width, **kwargs)

1D Box filter kernel.

Box2DKernel(width, **kwargs)

2D Box filter kernel.

CustomKernel(array)

Create filter kernel from list or array.

Gaussian1DKernel(stddev, **kwargs)

1D Gaussian filter kernel.

Gaussian2DKernel(x_stddev[, y_stddev, theta])

2D Gaussian filter kernel.

Kernel(array)

Convolution kernel base class.

Kernel1D([model, x_size, array])

Base class for 1D filter kernels.

Kernel2D([model, x_size, y_size, array])

Base class for 2D filter kernels.

KernelSizeError

Called when size of kernels is even.

Model1DKernel(model, **kwargs)

Create kernel from 1D model.

Model2DKernel(model, **kwargs)

Create kernel from 2D model.

Moffat2DKernel(gamma, alpha, **kwargs)

2D Moffat kernel.

RickerWavelet1DKernel(width, **kwargs)

1D Ricker wavelet filter kernel (sometimes known as a "Mexican Hat" kernel).

RickerWavelet2DKernel(width, **kwargs)

2D Ricker wavelet filter kernel (sometimes known as a "Mexican Hat" kernel).

Ring2DKernel(radius_in, width, **kwargs)

2D Ring filter kernel.

Tophat2DKernel(radius, **kwargs)

2D Tophat filter kernel.

Trapezoid1DKernel(width[, slope])

1D trapezoid kernel.

TrapezoidDisk2DKernel(radius[, slope])

2D trapezoid kernel.