SmoothlyBrokenPowerLaw1D

class astropy.modeling.powerlaws.SmoothlyBrokenPowerLaw1D(amplitude=1, x_break=1, alpha_1=-2, alpha_2=2, delta=1, **kwargs)

Bases: Fittable1DModel

One dimensional smoothly broken power law model.

Parameters:

amplitudepython:float

Model amplitude at the break point.

x_breakpython:float

Break point.

alpha_1python:float

Power law index for x << x_break.

alpha_2python:float

Power law index for x >> x_break.

deltapython:float

Smoothness parameter.

See also

BrokenPowerLaw1D

Notes

Model formula (with \(A\) for amplitude, \(x_b\) for x_break, \(\alpha_1\) for alpha_1, \(\alpha_2\) for alpha_2 and \(\Delta\) for delta):

\[f(x) = A \left( \frac{x}{x_b} \right) ^ {-\alpha_1} \left\{ \frac{1}{2} \left[ 1 + \left( \frac{x}{x_b}\right)^{1 / \Delta} \right] \right\}^{(\alpha_1 - \alpha_2) \Delta}\]

The change of slope occurs between the values \(x_1\) and \(x_2\) such that:

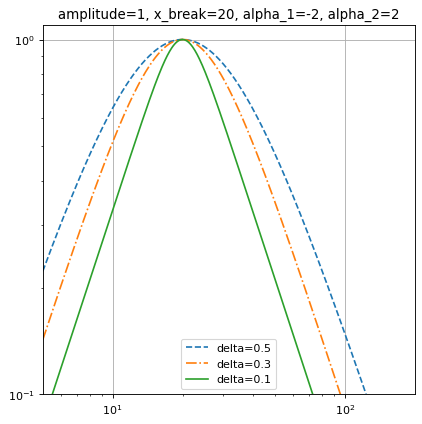
\[\log_{10} \frac{x_2}{x_b} = \log_{10} \frac{x_b}{x_1} \sim \Delta\]

At values \(x \lesssim x_1\) and \(x \gtrsim x_2\) the model is approximately a simple power law with index \(\alpha_1\) and \(\alpha_2\) respectively. The two power laws are smoothly joined at values \(x_1 < x < x_2\), hence the \(\Delta\) parameter sets the “smoothness” of the slope change.

The delta parameter is bounded to values greater than 1e-3 (corresponding to \(x_2 / x_1 \gtrsim 1.002\)) to avoid overflow errors.

The amplitude parameter is bounded to positive values since this model is typically used to represent positive quantities.

Examples

import numpy as np
import matplotlib.pyplot as plt
from astropy.modeling import models

x = np.logspace(0.7, 2.3, 500)
f = models.SmoothlyBrokenPowerLaw1D(amplitude=1, x_break=20,
                                    alpha_1=-2, alpha_2=2)

plt.figure()
plt.title("amplitude=1, x_break=20, alpha_1=-2, alpha_2=2")

f.delta = 0.5
plt.loglog(x, f(x), '--', label='delta=0.5')

f.delta = 0.3
plt.loglog(x, f(x), '-.', label='delta=0.3')

f.delta = 0.1
plt.loglog(x, f(x), label='delta=0.1')

plt.axis([x.min(), x.max(), 0.1, 1.1])
plt.legend(loc='lower center')
plt.grid(True)
plt.show()

(png, svg, pdf)

Attributes Summary

alpha_1
alpha_2
amplitude
delta
input_units	This property is used to indicate what units or sets of units the evaluate method expects, and returns a dictionary mapping inputs to units (or None if any units are accepted).
param_names	Names of the parameters that describe models of this type.
x_break

Methods Summary

evaluate(x, amplitude, x_break, alpha_1, ...)	One dimensional smoothly broken power law model function
fit_deriv(x, amplitude, x_break, alpha_1, ...)	One dimensional smoothly broken power law derivative with respect to parameters

Attributes Documentation

alpha_1 = Parameter('alpha_1', value=-2.0)

alpha_2 = Parameter('alpha_2', value=2.0)

amplitude = Parameter('amplitude', value=1.0, bounds=(0, None))

delta = Parameter('delta', value=1.0, bounds=(0.001, None))

input_units

param_names = ('amplitude', 'x_break', 'alpha_1', 'alpha_2', 'delta')

Names of the parameters that describe models of this type.

The parameters in this tuple are in the same order they should be passed in when initializing a model of a specific type. Some types of models, such as polynomial models, have a different number of parameters depending on some other property of the model, such as the degree.

When defining a custom model class the value of this attribute is automatically set by the Parameter attributes defined in the class body.

x_break = Parameter('x_break', value=1.0)

Methods Documentation

static evaluate(x, amplitude, x_break, alpha_1, alpha_2, delta)

One dimensional smoothly broken power law model function

static fit_deriv(x, amplitude, x_break, alpha_1, alpha_2, delta)

One dimensional smoothly broken power law derivative with respect to parameters