Voigt1D

class astropy.modeling.functional_models.Voigt1D(x_0=0, amplitude_L=1, fwhm_L=0.6366197723675814, fwhm_G=0.6931471805599453, method='humlicek2', **kwargs)

Bases: Fittable1DModel

One dimensional model for the Voigt profile.

Parameters:

x_0python:float or Quantity

Position of the peak

amplitude_Lpython:float or Quantity.

The Lorentzian amplitude (peak of the associated Lorentz function) - for a normalized profile (integrating to 1), set amplitude_L = 2 / (np.pi * fwhm_L)

fwhm_Lpython:float or Quantity

The Lorentzian full width at half maximum

fwhm_Gpython:float or Quantity.

The Gaussian full width at half maximum

methodpython:str, optional

Algorithm for computing the complex error function; one of ‘Humlicek2’ (default, fast and generally more accurate than rtol=3.e-5) or ‘Scipy’, alternatively ‘wofz’ (requires scipy, almost as fast and reference in accuracy).

Other Parameters:

fixeda python:dict, optional

A dictionary {parameter_name: boolean} of parameters to not be varied during fitting. True means the parameter is held fixed. Alternatively the fixed property of a parameter may be used.

tiedpython:dict, optional

A dictionary {parameter_name: callable} of parameters which are linked to some other parameter. The dictionary values are callables providing the linking relationship. Alternatively the tied property of a parameter may be used.

boundspython:dict, optional

A dictionary {parameter_name: value} of lower and upper bounds of parameters. Keys are parameter names. Values are a list or a tuple of length 2 giving the desired range for the parameter. Alternatively, the min and max properties of a parameter may be used.

eqconspython:list, optional

A list of functions of length n such that eqcons[j](x0,*args) == 0.0 in a successfully optimized problem.

ineqconspython:list, optional

A list of functions of length n such that ieqcons[j](x0,*args) >= 0.0 is a successfully optimized problem.

See also

Gaussian1D, Lorentz1D

Notes

Either all or none of input x, position x_0 and the fwhm_* must be provided consistently with compatible units or as unitless numbers. Voigt function is calculated as real part of the complex error function computed from either Humlicek’s rational approximations (JQSRT 21:309, 1979; 27:437, 1982) following Schreier 2018 (MNRAS 479, 3068; and hum2zpf16m from his cpfX.py module); or wofz (implementing ‘Faddeeva.cc’).

Examples

import numpy as np
from astropy.modeling.models import Voigt1D
import matplotlib.pyplot as plt

plt.figure()
x = np.arange(0, 10, 0.01)
v1 = Voigt1D(x_0=5, amplitude_L=10, fwhm_L=0.5, fwhm_G=0.9)
plt.plot(x, v1(x))
plt.show()

(png, svg, pdf)

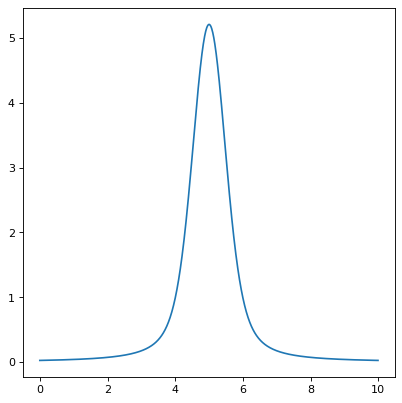
Attributes Summary

amplitude_L
fwhm_G
fwhm_L
input_units	This property is used to indicate what units or sets of units the evaluate method expects, and returns a dictionary mapping inputs to units (or None if any units are accepted).
param_names	Names of the parameters that describe models of this type.
sqrt_ln2
sqrt_ln2pi
sqrt_pi
x_0

Methods Summary

evaluate(x, x_0, amplitude_L, fwhm_L, fwhm_G)	One dimensional Voigt function scaled to Lorentz peak amplitude.
fit_deriv(x, x_0, amplitude_L, fwhm_L, fwhm_G)	Derivative of the one dimensional Voigt function with respect to parameters.

Attributes Documentation

amplitude_L = Parameter('amplitude_L', value=1.0)

fwhm_G = Parameter('fwhm_G', value=0.6931471805599453)

fwhm_L = Parameter('fwhm_L', value=0.6366197723675814)

input_units

param_names = ('x_0', 'amplitude_L', 'fwhm_L', 'fwhm_G')

Names of the parameters that describe models of this type.

The parameters in this tuple are in the same order they should be passed in when initializing a model of a specific type. Some types of models, such as polynomial models, have a different number of parameters depending on some other property of the model, such as the degree.

When defining a custom model class the value of this attribute is automatically set by the Parameter attributes defined in the class body.

sqrt_ln2 = 0.8325546111576977

sqrt_ln2pi = 1.475664626635606

sqrt_pi = 1.7724538509055159

x_0 = Parameter('x_0', value=0.0)

Methods Documentation

evaluate(x, x_0, amplitude_L, fwhm_L, fwhm_G)

One dimensional Voigt function scaled to Lorentz peak amplitude.

fit_deriv(x, x_0, amplitude_L, fwhm_L, fwhm_G)

Derivative of the one dimensional Voigt function with respect to parameters.