Gaussian2DKernel

class astropy.convolution.Gaussian2DKernel(x_stddev, y_stddev=None, theta=0.0, **kwargs)

Bases: Kernel2D

2D Gaussian filter kernel.

The Gaussian filter is a filter with great smoothing properties. It is isotropic and does not produce artifacts.

The generated kernel is normalized so that it integrates to 1.

Parameters:

x_stddevpython:float

Standard deviation of the Gaussian in x before rotating by theta.

y_stddevpython:float

Standard deviation of the Gaussian in y before rotating by theta.

thetapython:float or Quantity [:ref: ‘angle’]

Rotation angle. If passed as a float, it is assumed to be in radians. The rotation angle increases counterclockwise.

x_sizepython:int, optional

Size in x direction of the kernel array. Default = ⌊8*stddev + 1⌋.

y_sizepython:int, optional

Size in y direction of the kernel array. Default = ⌊8*stddev + 1⌋.

mode{‘center’, ‘linear_interp’, ‘oversample’, ‘integrate’}, optional

One of the following discretization modes:

• ‘center’ (default)

  Discretize model by taking the value at the center of the bin.

• ‘linear_interp’

  Discretize model by performing a bilinear interpolation between the values at the corners of the bin.

• ‘oversample’

  Discretize model by taking the average on an oversampled grid.

• ‘integrate’

  Discretize model by integrating the model over the bin.

factornumber, optional

Factor of oversampling. Default factor = 10.

See also

Box2DKernel, Tophat2DKernel, RickerWavelet2DKernel, Ring2DKernel

TrapezoidDisk2DKernel, AiryDisk2DKernel, Moffat2DKernel

Examples

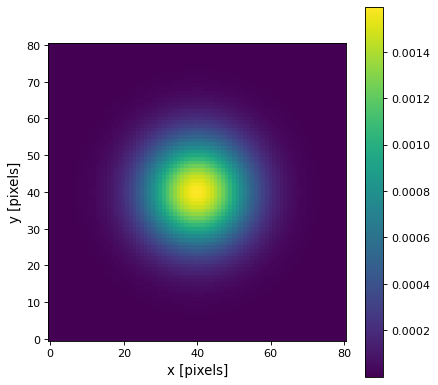
Kernel response:

import matplotlib.pyplot as plt
from astropy.convolution import Gaussian2DKernel
gaussian_2D_kernel = Gaussian2DKernel(10)
plt.imshow(gaussian_2D_kernel, interpolation='none', origin='lower')
plt.xlabel('x [pixels]')
plt.ylabel('y [pixels]')
plt.colorbar()
plt.show()

(png, svg, pdf)