Phase diagrams and Pourbaix diagrams¶
- class ase.phasediagram.PhaseDiagram(references, filter='', verbose=True)[source]¶
Phase-diagram.
- references: list of (name, energy) tuples
List of references. The energy must be the total energy and not energy per atom. The names can also be dicts like
{'Zn': 1, 'O': 2}which would be equivalent to'ZnO2'.- filter: str or list of str
Use only those references that match the given filter. Example:
filter='ZnO'will select those that contain zinc or oxygen.- verbose: bool
Write information.
Here is a simple example using some made up numbers for Cu-Au alloys:
>>> from ase.phasediagram import PhaseDiagram
>>> refs = [('Cu', 0.0),
... ('Au', 0.0),
... ('CuAu', -0.5),
... ('Cu2Au', -0.7),
... ('Cu2Au', -0.2)]
>>> pd = PhaseDiagram(refs)
Species: Au, Cu
References: 5
0 Cu 0.000
1 Au 0.000
2 CuAu -0.500
3 Cu2Au -0.700
4 CuAu2 -0.200
Simplices: 3
The convex hull looks like this:
>>> pd.plot(show=True)
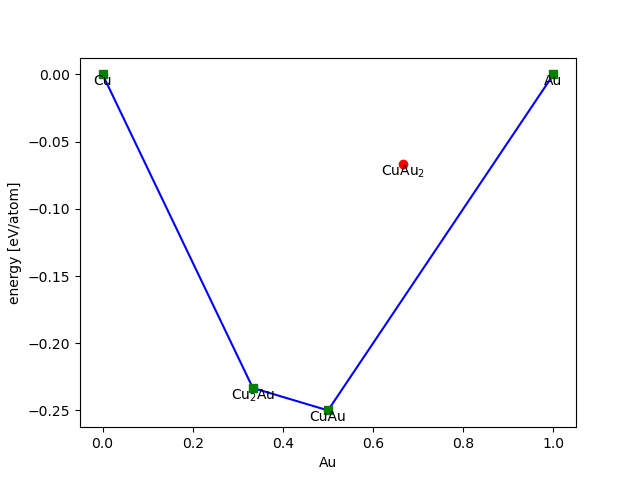
- PhaseDiagram.plot(ax=None, dims=None, show=False, **plotkwargs)[source]¶
Make 2-d or 3-d plot of datapoints and convex hull.
Default is 2-d for 2- and 3-component diagrams and 3-d for a 4-component diagram.
If you want to see what Cu3Au will decompose into, you can use the
decompose() method:
>>> energy, indices, coefs = pd.decompose('Cu3Au')
reference coefficient energy
------------------------------------
Cu 1 0.000
Cu2Au 1 -0.700
------------------------------------
Total energy: -0.700
------------------------------------
>>> print(energy, indices, coefs)
(-0.69999999999999996, array([0, 3], dtype=int32), array([ 1., 1.]))
Alternatively, one could have used pd.decompose(Cu=3, Au=1).
- PhaseDiagram.decompose(formula=None, **kwargs)[source]¶
Find the combination of the references with the lowest energy.
- formula: str
Stoichiometry. Example:
'ZnO'. Can also be given as keyword arguments:decompose(Zn=1, O=1).
Example:
pd = PhaseDiagram(...) pd.decompose(Zn=1, O=3)
Returns energy, indices of references and coefficients.
Here is an example (see ktao.py) with three components using
plot(dims=2) and plot(dims=3):


Pourbaix diagrams¶
Let’s create a Pourbaix diagram for ZnO from experimental numbers.
>>> from ase.phasediagram import Pourbaix, solvated
>>> refs = solvated('Zn')
>>> print(refs)
[('HZnO2-(aq)', -4.801274772854441), ('ZnO2--(aq)', -4.0454382546928365), ('ZnOH+(aq)', -3.5207324675582736), ('ZnO(aq)', -2.9236086089762137), ('H2O(aq)', -2.458311658897383), ('Zn++(aq)', -1.5264168353005447), ('H+(aq)', 0.0)]
We use the solvated() function to get solvation energies for zinc
containing molecules (plus water and a proton):
- ase.phasediagram.solvated(symbols)[source]¶
Extract solvation energies from database.
- symbols: str
Extract only those molecules that contain the chemical elements given by the symbols string (plus water and H+).
Data from:
Johnson JW, Oelkers EH, Helgeson HC (1992) Comput Geosci 18(7):899. doi:10.1016/0098-3004(92)90029-Q
and:
Pourbaix M (1966) Atlas of electrochemical equilibria in aqueous solutions. No. v. 1 in Atlas of Electrochemical Equilibria in Aqueous Solutions. Pergamon Press, New York.
Returns list of (name, energy) tuples.
We add two solids and one more dissolved molecule to the references and create
a Pourbaix object:
>>> refs += [('Zn', 0.0), ('ZnO', -3.323), ('ZnO2(aq)', -2.921)]
>>> pb = Pourbaix(refs, Zn=1, O=1)
To see what ZnO will decompose() to at a potential of 1 eV
and a pH of 9.0, we do this:
>>> coefs, energy = pb.decompose(1.0, 9.0)
0 HZnO2-(aq) -5.158
1 ZnO2--(aq) -4.403
2 ZnOH+(aq) -3.878
3 ZnO(aq) -3.281
4 H2O(aq) -2.458
5 Zn++(aq) -1.884
6 H+(aq) -0.536
7 Zn 0.000
8 ZnO -3.323
9 ZnO2(aq) -3.278
10 e- -1.000
reference coefficient energy
------------------------------------
H2O(aq) -1 -2.458
H+(aq) 2 -0.536
ZnO2(aq) 1 -3.278
e- 2 -1.000
------------------------------------
Total energy: -3.891
------------------------------------
>>> print(coefs, energy)
(array([ 0.00000000e+00, 0.00000000e+00, 6.66133815e-16,
0.00000000e+00, -1.00000000e+00, 0.00000000e+00,
2.00000000e+00, 0.00000000e+00, 0.00000000e+00,
1.00000000e+00, 2.00000000e+00]), -3.8913313372636829)
The full diagram() is calculated like this:
>>> import numpy as np
>>> U = np.linspace(-2, 2, 200)
>>> pH = np.linspace(-2, 16, 300)
>>> d, names, text = pb.diagram(U, pH, plot=True)
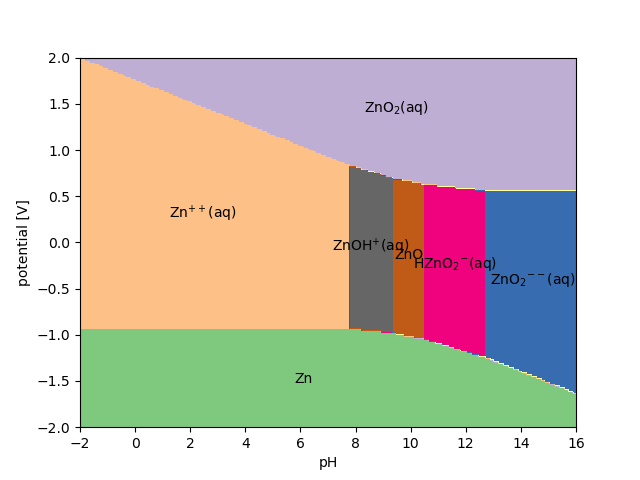
- class ase.phasediagram.Pourbaix(references, formula=None, T=300.0, **kwargs)[source]¶
Pourbaix object.
- references: list of (name, energy) tuples
Examples of names: ZnO2, H+(aq), H2O(aq), Zn++(aq), …
- formula: str
Stoichiometry. Example:
'ZnO'. Can also be given as keyword arguments:Pourbaix(refs, Zn=1, O=1).- T: float
Temperature in Kelvin.
- decompose(U, pH, verbose=True, concentration=1e-06)[source]¶
Decompose material.
- U: float
Potential in V.
- pH: float
pH value.
- verbose: bool
Default is True.
- concentration: float
Concentration of solvated references.
Returns optimal coefficients and energy:
>>> from ase.phasediagram import Pourbaix, solvated >>> refs = solvated('CoO') + [ ... ('Co', 0.0), ... ('CoO', -2.509), ... ('Co3O4', -9.402)] >>> pb = Pourbaix(refs, Co=3, O=4) >>> coefs, energy = pb.decompose(U=1.5, pH=0, ... concentration=1e-6, ... verbose=True) 0 HCoO2-(aq) -3.974 1 CoO2--(aq) -3.098 2 H2O(aq) -2.458 3 CoOH+(aq) -2.787 4 CoO(aq) -2.265 5 CoOH++(aq) -1.355 6 Co++(aq) -0.921 7 H+(aq) 0.000 8 Co+++(aq) 1.030 9 Co 0.000 10 CoO -2.509 11 Co3O4 -9.402 12 e- -1.500 reference coefficient energy ------------------------------------ H2O(aq) 4 -2.458 Co++(aq) 3 -0.921 H+(aq) -8 0.000 e- -2 -1.500 ------------------------------------ Total energy: -9.596 ------------------------------------
- diagram(U, pH, plot=True, show=False, ax=None)[source]¶
Calculate Pourbaix diagram.
- U: list of float
Potentials in V.
- pH: list of float
pH values.
- plot: bool
Create plot.
- show: bool
Open graphical window and show plot.
- ax: matplotlib axes object
When creating plot, plot onto the given axes object. If none given, plot onto the current one.