The Atoms object

The Atoms object is a collection of atoms. Here is how to define a CO molecule:

from ase import Atoms
d = 1.1
co = Atoms('CO', positions=[(0, 0, 0), (0, 0, d)])

Here, the first argument specifies the type of the atoms and we used the positions keywords to specify their positions. Other possible keywords are: numbers, tags, momenta, masses, magmoms and charges.

Here is how you could make an infinite gold wire with a bond length of 2.9 Å:

from ase import Atoms
d = 2.9
L = 10.0
wire = Atoms('Au',
             positions=[[0, L / 2, L / 2]],
             cell=[d, L, L],
             pbc=[1, 0, 0])

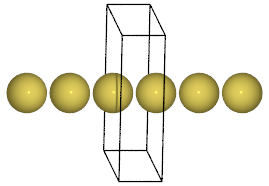
Here, two more optional keyword arguments were used:

cell: Unit cell size

This can be a sequence of three numbers for an orthorhombic unit cell or three by three numbers for a general unit cell (a sequence of three sequences of three numbers) or six numbers (three legths and three angles in degrees). The default value is [0,0,0] which is the same as [[0,0,0],[0,0,0],[0,0,0]] or [0,0,0,90,90,90] meaning that none of the three lattice vectors are defined.

pbc: Periodic boundary conditions

The default value is False - a value of True would give periodic boundary conditions along all three axes. It is possible to give a sequence of three booleans to specify periodicity along specific axes.

You can also use the following methods to work with the unit cell and the boundary conditions: set_pbc(), set_cell(), get_cell(), and get_pbc().

Working with the array methods of Atoms objects

Like with a single Atom the properties of a collection of atoms can be accessed and changed with get- and set-methods. For example the positions of the atoms can be addressed as

>>> from ase import Atoms
>>> atoms = Atoms('N3', [(0, 0, 0), (1, 0, 0), (0, 0, 1)])
>>> atoms.get_positions()
array([[ 0.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 0.,  0.,  1.]])
>>> atoms.set_positions([(2, 0, 0), (0, 2, 2), (2, 2, 0)])
>>> atoms.get_positions()
array([[ 2.,  0.,  0.],
       [ 0.,  2.,  2.],
       [ 2.,  2.,  0.]])

Here is the full list of the get/set methods operating on all the atoms at once. The get methods return an array of quantities, one for each atom; the set methods take similar arrays. E.g. get_positions() return N * 3 numbers, get_atomic_numbers() return N integers.

These methods return copies of the internal arrays. It is thus safe to modify the returned arrays.

get_atomic_numbers()	set_atomic_numbers()
get_initial_charges()	set_initial_charges()
get_charges()
get_chemical_symbols()	set_chemical_symbols()
get_initial_magnetic_moments()	set_initial_magnetic_moments()
get_magnetic_moments()
get_masses()	set_masses()
get_momenta()	set_momenta()
get_forces()
get_positions()	set_positions()
get_potential_energies()
get_scaled_positions()	set_scaled_positions()
get_stresses()
get_tags()	set_tags()
get_velocities()	set_velocities()

There are also a number of get/set methods that operate on quantities common to all the atoms or defined for the collection of atoms:

get_calculator()	set_calculator()
get_cell()	set_cell()
get_cell_lengths_and_angles()
get_center_of_mass()
get_kinetic_energy()
get_magnetic_moment()
get_global_number_of_atoms()
get_pbc()	set_pbc()
get_potential_energy()
get_stress()
get_total_energy()
get_volume()

Unit cell and boundary conditions

The Atoms object holds a unit cell. The unit cell is a Cell object which resembles a 3x3 matrix when used with numpy, arithmetic operations, or indexing:

>>> atoms.cell
Cell([0.0, 0.0, 0.0], pbc=False)
>>> atoms.cell[:]
array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]])

The cell can be defined or changed using the set_cell() method. Changing the unit cell does per default not move the atoms:

>>> import numpy as np
>>> atoms.set_cell(2 * np.identity(3))
>>> atoms.get_cell()
Cell([2.0, 2.0, 2.0], pbc=False)
>>> atoms.set_positions([(2, 0, 0), (1, 1, 0), (2, 2, 0)])
>>> atoms.get_positions()
array([[ 2.,  0.,  0.],
       [ 1.,  1.,  0.],
       [ 2.,  2.,  0.]])

However if we set scale_atoms=True the atomic positions are scaled with the unit cell:

>>> atoms.set_cell(np.identity(3), scale_atoms=True)
>>> atoms.get_positions()
array([[ 1. ,  0. ,  0. ],
       [ 0.5,  0.5,  0. ],
       [ 1. ,  1. ,  0. ]])

The set_pbc() method specifies whether periodic boundary conditions are to be used in the directions of the three vectors of the unit cell. A slab calculation with periodic boundary conditions in x and y directions and free boundary conditions in the z direction is obtained through

>>> atoms.set_pbc((True, True, False))

or

>>> atoms.pbc = (True, True, False)

Special attributes

It is also possible to work directly with the attributes positions, numbers, pbc and cell. Here we change the position of the 2nd atom (which has count number 1 because Python starts counting at zero) and the type of the first atom:

>>> atoms.positions *= 2
>>> atoms.positions[1] = (1, 1, 0)
>>> atoms.get_positions()
array([[ 2.,  0.,  0.],
       [ 1.,  1.,  0.],
       [ 2.,  2.,  0.]])
>>> atoms.positions
array([[ 2.,  0.,  0.],
       [ 1.,  1.,  0.],
       [ 2.,  2.,  0.]])
>>> atoms.numbers
array([7, 7, 7])
>>> atoms.numbers[0] = 13
>>> atoms.get_chemical_symbols()
['Al', 'N', 'N']

The atomic numbers can also be edited using the symbols shortcut (see also ase.symbols.Symbols):

>>> atoms.symbols
Symbols('AlN2')
>>> atoms.symbols[2] = 'Cu'
>>> atoms.symbols
Symbols('AlNCu')
>>> atoms.numbers
array([13,  7, 29])

Check for periodic boundary conditions:

>>> atoms.pbc  # equivalent to atoms.get_pbc()
array([ True,  True, False], dtype=bool)
>>> atoms.pbc.any()
True
>>> atoms.pbc[2] = 1
>>> atoms.pbc
array([ True,  True,  True], dtype=bool)

Hexagonal unit cell:

>>> atoms.cell = [2.5, 2.5, 15, 90, 90, 120]

Attributes that can be edited directly are:

• numbers()

• symbols()

• positions()

• cell()

• pbc()

• constraints()

Adding a calculator

A calculator can be attached to the atoms with the purpose of calculating energies and forces on the atoms. ASE works with many different ase.calculators.

A calculator object calc is attached to the atoms like this:

>>> atoms.calc = calc

After the calculator has been appropriately setup the energy of the atoms can be obtained through

>>> atoms.get_potential_energy()

The term “potential energy” here means for example the total energy of a DFT calculation, which includes both kinetic, electrostatic, and exchange-correlation energy for the electrons. The reason it is called potential energy is that the atoms might also have a kinetic energy (from the moving nuclei) and that is obtained with

>>> atoms.get_kinetic_energy()

In case of a DFT calculator, it is up to the user to check exactly what the get_potential_energy() method returns. For example it may be the result of a calculation with a finite temperature smearing of the occupation numbers extrapolated to zero temperature. More about this can be found for the different ase.calculators.

The following methods can only be called if a calculator is present:

• get_potential_energy()

• get_potential_energies()

• get_forces()

• get_stress()

• get_stresses()

• get_total_energy()

• get_magnetic_moments()

• get_magnetic_moment()

Not all of these methods are supported by all calculators.

List-methods

method	example
+	wire2 = wire + co
+=, extend()	wire += co wire.extend(co)
append()	wire.append(Atom('H'))
*	wire3 = wire * (3, 1, 1)
*=, repeat()	wire *= (3, 1, 1) wire.repeat((3, 1, 1))
len	len(co)
del	del wire3[0] del wire3[[1,3]]
pop()	oxygen = wire2.pop()

Note that the del method can be used with the more powerful numpy-style indexing, as in the second example above. This can be combined with python list comprehension in order to selectively delete atoms within an ASE Atoms object. For example, the below code creates an ethanol molecule and subsequently strips all the hydrogen atoms from it:

from ase.build import molecule
atoms = molecule('CH3CH2OH')
del atoms[[atom.index for atom in atoms if atom.symbol=='H']]

Other methods

• center()

• wrap()

• translate()

• rotate()

• euler_rotate()

• get_dihedral()

• set_dihedral()

• rotate_dihedral()

• rattle()

• set_constraint()

• set_distance()

• copy()

• get_center_of_mass()

• get_distance()

• get_distances()

• get_all_distances()

• get_volume()

• has()

• edit()

List of all Methods

class ase.Atoms(symbols=None, positions=None, numbers=None, tags=None, momenta=None, masses=None, magmoms=None, charges=None, scaled_positions=None, cell=None, pbc=None, celldisp=None, constraint=None, calculator=None, info=None, velocities=None)

Atoms object.

The Atoms object can represent an isolated molecule, or a periodically repeated structure. It has a unit cell and there may be periodic boundary conditions along any of the three unit cell axes. Information about the atoms (atomic numbers and position) is stored in ndarrays. Optionally, there can be information about tags, momenta, masses, magnetic moments and charges.

In order to calculate energies, forces and stresses, a calculator object has to attached to the atoms object.

Parameters:

symbols: str (formula) or list of str

Can be a string formula, a list of symbols or a list of Atom objects. Examples: ‘H2O’, ‘COPt12’, [‘H’, ‘H’, ‘O’], [Atom(‘Ne’, (x, y, z)), …].

positions: list of xyz-positions

Atomic positions. Anything that can be converted to an ndarray of shape (n, 3) will do: [(x1,y1,z1), (x2,y2,z2), …].

scaled_positions: list of scaled-positions

Like positions, but given in units of the unit cell. Can not be set at the same time as positions.

numbers: list of int

Atomic numbers (use only one of symbols/numbers).

tags: list of int

Special purpose tags.

momenta: list of xyz-momenta

Momenta for all atoms.

masses: list of float

Atomic masses in atomic units.

magmoms: list of float or list of xyz-values

Magnetic moments. Can be either a single value for each atom for collinear calculations or three numbers for each atom for non-collinear calculations.

charges: list of float

Initial atomic charges.

cell: 3x3 matrix or length 3 or 6 vector

Unit cell vectors. Can also be given as just three numbers for orthorhombic cells, or 6 numbers, where first three are lengths of unit cell vectors, and the other three are angles between them (in degrees), in following order: [len(a), len(b), len(c), angle(b,c), angle(a,c), angle(a,b)]. First vector will lie in x-direction, second in xy-plane, and the third one in z-positive subspace. Default value: [0, 0, 0].

celldisp: Vector

Unit cell displacement vector. To visualize a displaced cell around the center of mass of a Systems of atoms. Default value = (0,0,0)

pbc: one or three bool

Periodic boundary conditions flags. Examples: True, False, 0, 1, (1, 1, 0), (True, False, False). Default value: False.

constraint: constraint object(s)

Used for applying one or more constraints during structure optimization.

calculator: calculator object

Used to attach a calculator for calculating energies and atomic forces.

info: dict of key-value pairs

Dictionary of key-value pairs with additional information about the system. The following keys may be used by ase:

• spacegroup: Spacegroup instance

• unit_cell: ‘conventional’ | ‘primitive’ | int | 3 ints

• adsorbate_info: Information about special adsorption sites

Items in the info attribute survives copy and slicing and can be stored in and retrieved from trajectory files given that the key is a string, the value is JSON-compatible and, if the value is a user-defined object, its base class is importable. One should not make any assumptions about the existence of keys.

Examples:

These three are equivalent:

>>> d = 1.104  # N2 bondlength
>>> a = Atoms('N2', [(0, 0, 0), (0, 0, d)])
>>> a = Atoms(numbers=[7, 7], positions=[(0, 0, 0), (0, 0, d)])
>>> a = Atoms([Atom('N', (0, 0, 0)), Atom('N', (0, 0, d))])

FCC gold:

>>> a = 4.05  # Gold lattice constant
>>> b = a / 2
>>> fcc = Atoms('Au',
...             cell=[(0, b, b), (b, 0, b), (b, b, 0)],
...             pbc=True)

Hydrogen wire:

>>> d = 0.9  # H-H distance
>>> h = Atoms('H', positions=[(0, 0, 0)],
...           cell=(d, 0, 0),
...           pbc=(1, 0, 0))

append(atom)

Append atom to end.

property calc

Calculator object.

property cell

The ase.cell.Cell for direct manipulation.

center(vacuum=None, axis=(0, 1, 2), about=None)

Center atoms in unit cell.

Centers the atoms in the unit cell, so there is the same amount of vacuum on all sides.

vacuum: float (default: None)

If specified adjust the amount of vacuum when centering. If vacuum=10.0 there will thus be 10 Angstrom of vacuum on each side.

axis: int or sequence of ints

Axis or axes to act on. Default: Act on all axes.

about: float or array (default: None)

If specified, center the atoms about <about>. I.e., about=(0., 0., 0.) (or just “about=0.”, interpreted identically), to center about the origin.

property constraints

Constraints of the atoms.

copy()

Return a copy.

edit()

Modify atoms interactively through ASE’s GUI viewer.

Conflicts leading to undesirable behaviour might arise when matplotlib has been pre-imported with certain incompatible backends and while trying to use the plot feature inside the interactive GUI. To circumvent, please set matplotlib.use(‘gtk’) before calling this method.

euler_rotate(phi=0.0, theta=0.0, psi=0.0, center=(0, 0, 0))

Rotate atoms via Euler angles (in degrees).

See e.g http://mathworld.wolfram.com/EulerAngles.html for explanation.

Parameters:

center :

The point to rotate about. A sequence of length 3 with the coordinates, or ‘COM’ to select the center of mass, ‘COP’ to select center of positions or ‘COU’ to select center of cell.

phi :

The 1st rotation angle around the z axis.

theta :

Rotation around the x axis.

psi :

2nd rotation around the z axis.

extend(other)

Extend atoms object by appending atoms from other.

classmethod fromdict(dct)

Rebuild atoms object from dictionary representation (todict).

get_all_distances(mic=False, vector=False)

Return distances of all of the atoms with all of the atoms.

Use mic=True to use the Minimum Image Convention.

get_angle(a1, a2, a3, mic=False)

Get angle formed by three atoms.

Calculate angle in degrees between the vectors a2->a1 and a2->a3.

Use mic=True to use the Minimum Image Convention and calculate the angle across periodic boundaries.

get_angles(indices, mic=False)

Get angle formed by three atoms for multiple groupings.

Calculate angle in degrees between vectors between atoms a2->a1 and a2->a3, where a1, a2, and a3 are in each row of indices.

Use mic=True to use the Minimum Image Convention and calculate the angle across periodic boundaries.

get_angular_momentum()

Get total angular momentum with respect to the center of mass.

get_array(name, copy=True)

Get an array.

Returns a copy unless the optional argument copy is false.

get_atomic_numbers()

Get integer array of atomic numbers.

get_calculator()

Get currently attached calculator object.

Please use the equivalent atoms.calc instead of atoms.get_calculator().

get_cell(complete=False)

Get the three unit cell vectors as a \(class\):ase.cell.Cell` object.

The Cell object resembles a 3x3 ndarray, and cell[i, j] is the jth Cartesian coordinate of the ith cell vector.

get_cell_lengths_and_angles()

Get unit cell parameters. Sequence of 6 numbers.

First three are unit cell vector lengths and second three are angles between them:

[len(a), len(b), len(c), angle(b,c), angle(a,c), angle(a,b)]

in degrees.

get_celldisp()

Get the unit cell displacement vectors.

get_center_of_mass(scaled=False)

Get the center of mass.

If scaled=True the center of mass in scaled coordinates is returned.

get_charges()

Get calculated charges.

get_chemical_formula(mode='hill', empirical=False)

Get the chemical formula as a string based on the chemical symbols.

Parameters:

mode: str

There are four different modes available:

‘all’: The list of chemical symbols are contracted to a string, e.g. [‘C’, ‘H’, ‘H’, ‘H’, ‘O’, ‘H’] becomes ‘CHHHOH’.

‘reduce’: The same as ‘all’ where repeated elements are contracted to a single symbol and a number, e.g. ‘CHHHOCHHH’ is reduced to ‘CH3OCH3’.

‘hill’: The list of chemical symbols are contracted to a string following the Hill notation (alphabetical order with C and H first), e.g. ‘CHHHOCHHH’ is reduced to ‘C2H6O’ and ‘SOOHOHO’ to ‘H2O4S’. This is default.

‘metal’: The list of chemical symbols (alphabetical metals, and alphabetical non-metals)

empirical, bool (optional, default=False)

Divide the symbol counts by their greatest common divisor to yield an empirical formula. Only for mode \(metal\) and \(hill\).

get_chemical_symbols()

Get list of chemical symbol strings.

Equivalent to list(atoms.symbols).

get_dihedral(a0, a1, a2, a3, mic=False)

Calculate dihedral angle.

Calculate dihedral angle (in degrees) between the vectors a0->a1 and a2->a3.

Use mic=True to use the Minimum Image Convention and calculate the angle across periodic boundaries.

get_dihedrals(indices, mic=False)

Calculate dihedral angles.

Calculate dihedral angles (in degrees) between the list of vectors a0->a1 and a2->a3, where a0, a1, a2 and a3 are in each row of indices.

Use mic=True to use the Minimum Image Convention and calculate the angles across periodic boundaries.

get_dipole_moment()

Calculate the electric dipole moment for the atoms object.

Only available for calculators which has a get_dipole_moment() method.

get_distance(a0, a1, mic=False, vector=False)

Return distance between two atoms.

Use mic=True to use the Minimum Image Convention. vector=True gives the distance vector (from a0 to a1).

get_distances(a, indices, mic=False, vector=False)

Return distances of atom No.i with a list of atoms.

Use mic=True to use the Minimum Image Convention. vector=True gives the distance vector (from a to self[indices]).

get_forces(apply_constraint=True, md=False)

Calculate atomic forces.

Ask the attached calculator to calculate the forces and apply constraints. Use apply_constraint=False to get the raw forces.

For molecular dynamics (md=True) we don’t apply the constraint to the forces but to the momenta. When holonomic constraints for rigid linear triatomic molecules are present, ask the constraints to redistribute the forces within each triple defined in the constraints (required for molecular dynamics with this type of constraints).

get_global_number_of_atoms()

Returns the global number of atoms in a distributed-atoms parallel simulation.

DO NOT USE UNLESS YOU KNOW WHAT YOU ARE DOING!

Equivalent to len(atoms) in the standard ASE Atoms class. You should normally use len(atoms) instead. This function’s only purpose is to make compatibility between ASE and Asap easier to maintain by having a few places in ASE use this function instead. It is typically only when counting the global number of degrees of freedom or in similar situations.

get_initial_charges()

Get array of initial charges.

get_initial_magnetic_moments()

Get array of initial magnetic moments.

get_kinetic_energy()

Get the kinetic energy.

get_magnetic_moment()

Get calculated total magnetic moment.

get_magnetic_moments()

Get calculated local magnetic moments.

get_masses()

Get array of masses in atomic mass units.

get_momenta()

Get array of momenta.

get_moments_of_inertia(vectors=False)

Get the moments of inertia along the principal axes.

The three principal moments of inertia are computed from the eigenvalues of the symmetric inertial tensor. Periodic boundary conditions are ignored. Units of the moments of inertia are amu*angstrom**2.

get_number_of_atoms()

Deprecated, please do not use.

You probably want len(atoms). Or if your atoms are distributed, use (and see) get_global_number_of_atoms().

get_pbc()

Get periodic boundary condition flags.

get_positions(wrap=False, **wrap_kw)

Get array of positions.

Parameters:

wrap: bool

wrap atoms back to the cell before returning positions

wrap_kw: (keyword=value) pairs

optional keywords \(pbc\), \(center\), \(pretty_translation\), \(eps\), see ase.geometry.wrap_positions()

get_potential_energies()

Calculate the potential energies of all the atoms.

Only available with calculators supporting per-atom energies (e.g. classical potentials).

get_potential_energy(force_consistent=False, apply_constraint=True)

Calculate potential energy.

Ask the attached calculator to calculate the potential energy and apply constraints. Use apply_constraint=False to get the raw forces.

When supported by the calculator, either the energy extrapolated to zero Kelvin or the energy consistent with the forces (the free energy) can be returned.

get_properties(properties)

This method is experimental; currently for internal use.

get_reciprocal_cell()

Get the three reciprocal lattice vectors as a 3x3 ndarray.

Note that the commonly used factor of 2 pi for Fourier transforms is not included here.

get_scaled_positions(wrap=True)

Get positions relative to unit cell.

If wrap is True, atoms outside the unit cell will be wrapped into the cell in those directions with periodic boundary conditions so that the scaled coordinates are between zero and one.

If any cell vectors are zero, the corresponding coordinates are evaluated as if the cell were completed using cell.complete(). This means coordinates will be Cartesian as long as the non-zero cell vectors span a Cartesian axis or plane.

get_stress(voigt=True, apply_constraint=True, include_ideal_gas=False)

Calculate stress tensor.

Returns an array of the six independent components of the symmetric stress tensor, in the traditional Voigt order (xx, yy, zz, yz, xz, xy) or as a 3x3 matrix. Default is Voigt order.

The ideal gas contribution to the stresses is added if the atoms have momenta and include_ideal_gas is set to True.

get_stresses(include_ideal_gas=False, voigt=True)

Calculate the stress-tensor of all the atoms.

Only available with calculators supporting per-atom energies and stresses (e.g. classical potentials). Even for such calculators there is a certain arbitrariness in defining per-atom stresses.

The ideal gas contribution to the stresses is added if the atoms have momenta and include_ideal_gas is set to True.

get_tags()

Get integer array of tags.

get_temperature()

Get the temperature in Kelvin.

get_total_energy()

Get the total energy - potential plus kinetic energy.

get_velocities()

Get array of velocities.

get_volume()

Get volume of unit cell.

has(name)

Check for existence of array.

name must be one of: ‘tags’, ‘momenta’, ‘masses’, ‘initial_magmoms’, ‘initial_charges’.

new_array(name, a, dtype=None, shape=None)

Add new array.

If shape is not None, the shape of a will be checked.

property number_of_lattice_vectors

Number of (non-zero) lattice vectors.

property numbers

Attribute for direct manipulation of the atomic numbers.

property pbc

Reference to pbc-flags for in-place manipulations.

pop(i=-1)

Remove and return atom at index i (default last).

property positions

Attribute for direct manipulation of the positions.

rattle(stdev=0.001, seed=None, rng=None)

Randomly displace atoms.

This method adds random displacements to the atomic positions, taking a possible constraint into account. The random numbers are drawn from a normal distribution of standard deviation stdev.

For a parallel calculation, it is important to use the same seed on all processors!

repeat(rep)

Create new repeated atoms object.

The rep argument should be a sequence of three positive integers like (2,3,1) or a single integer (r) equivalent to (r,r,r).

rotate(a, v, center=(0, 0, 0), rotate_cell=False)

Rotate atoms based on a vector and an angle, or two vectors.

Parameters:

a = None:

Angle that the atoms is rotated around the vector ‘v’. ‘a’ can also be a vector and then ‘a’ is rotated into ‘v’.

v:

Vector to rotate the atoms around. Vectors can be given as strings: ‘x’, ‘-x’, ‘y’, … .

center = (0, 0, 0):

The center is kept fixed under the rotation. Use ‘COM’ to fix the center of mass, ‘COP’ to fix the center of positions or ‘COU’ to fix the center of cell.

rotate_cell = False:

If true the cell is also rotated.

Examples:

Rotate 90 degrees around the z-axis, so that the x-axis is rotated into the y-axis:

>>> atoms = Atoms()
>>> atoms.rotate(90, 'z')
>>> atoms.rotate(90, (0, 0, 1))
>>> atoms.rotate(-90, '-z')
>>> atoms.rotate('x', 'y')
>>> atoms.rotate((1, 0, 0), (0, 1, 0))

rotate_dihedral(a1, a2, a3, a4, angle=None, mask=None, indices=None)

Rotate dihedral angle.

Same usage as in ase.Atoms.set_dihedral(): Rotate a group by a predefined dihedral angle, starting from its current configuration.

set_angle(a1, a2=None, a3=None, angle=None, mask=None, indices=None, add=False)

Set angle (in degrees) formed by three atoms.

Sets the angle between vectors a2->*a1* and a2->*a3*.

If add is \(True\), the angle will be changed by the value given.

Same usage as in ase.Atoms.set_dihedral(). If mask and indices are given, indices overwrites mask. If mask and indices are not set, only a3 is moved.

set_array(name, a, dtype=None, shape=None)

Update array.

If shape is not None, the shape of a will be checked. If a is None, then the array is deleted.

set_atomic_numbers(numbers)

Set atomic numbers.

set_calculator(calc=None)

Attach calculator object.

Please use the equivalent atoms.calc = calc instead of this method.

set_cell(cell, scale_atoms=False, apply_constraint=True)

Set unit cell vectors.

Parameters:

cell: 3x3 matrix or length 3 or 6 vector

Unit cell. A 3x3 matrix (the three unit cell vectors) or just three numbers for an orthorhombic cell. Another option is 6 numbers, which describes unit cell with lengths of unit cell vectors and with angles between them (in degrees), in following order: [len(a), len(b), len(c), angle(b,c), angle(a,c), angle(a,b)]. First vector will lie in x-direction, second in xy-plane, and the third one in z-positive subspace.

scale_atoms: bool

Fix atomic positions or move atoms with the unit cell? Default behavior is to not move the atoms (scale_atoms=False).

apply_constraint: bool

Whether to apply constraints to the given cell.

Examples:

Two equivalent ways to define an orthorhombic cell:

>>> atoms = Atoms('He')
>>> a, b, c = 7, 7.5, 8
>>> atoms.set_cell([a, b, c])
>>> atoms.set_cell([(a, 0, 0), (0, b, 0), (0, 0, c)])

FCC unit cell:

>>> atoms.set_cell([(0, b, b), (b, 0, b), (b, b, 0)])

Hexagonal unit cell:

>>> atoms.set_cell([a, a, c, 90, 90, 120])

Rhombohedral unit cell:

>>> alpha = 77
>>> atoms.set_cell([a, a, a, alpha, alpha, alpha])

set_celldisp(celldisp)

Set the unit cell displacement vectors.

set_center_of_mass(com, scaled=False)

Set the center of mass.

If scaled=True the center of mass is expected in scaled coordinates. Constraints are considered for scaled=False.

set_chemical_symbols(symbols)

Set chemical symbols.

set_constraint(constraint=None)

Apply one or more constrains.

The constraint argument must be one constraint object or a list of constraint objects.

set_dihedral(a1, a2, a3, a4, angle, mask=None, indices=None)

Set the dihedral angle (degrees) between vectors a1->a2 and a3->a4 by changing the atom indexed by a4.

If mask is not None, all the atoms described in mask (read: the entire subgroup) are moved. Alternatively to the mask, the indices of the atoms to be rotated can be supplied. If both mask and indices are given, indices overwrites mask.

Important: If mask or indices is given and does not contain a4, a4 will NOT be moved. In most cases you therefore want to include a4 in mask/indices.

Example: the following defines a very crude ethane-like molecule and twists one half of it by 30 degrees.

>>> atoms = Atoms('HHCCHH', [[-1, 1, 0], [-1, -1, 0], [0, 0, 0],
...                          [1, 0, 0], [2, 1, 0], [2, -1, 0]])
>>> atoms.set_dihedral(1, 2, 3, 4, 210, mask=[0, 0, 0, 1, 1, 1])

set_distance(a0, a1, distance, fix=0.5, mic=False, mask=None, indices=None, add=False, factor=False)

Set the distance between two atoms.

Set the distance between atoms a0 and a1 to distance. By default, the center of the two atoms will be fixed. Use fix=0 to fix the first atom, fix=1 to fix the second atom and fix=0.5 (default) to fix the center of the bond.

If mask or indices are set (mask overwrites indices), only the atoms defined there are moved (see ase.Atoms.set_dihedral()).

When add is true, the distance is changed by the value given. In combination with factor True, the value given is a factor scaling the distance.

It is assumed that the atoms in mask/indices move together with a1. If fix=1, only a0 will therefore be moved.

set_initial_charges(charges=None)

Set the initial charges.

set_initial_magnetic_moments(magmoms=None)

Set the initial magnetic moments.

Use either one or three numbers for every atom (collinear or non-collinear spins).

set_masses(masses='defaults')

Set atomic masses in atomic mass units.

The array masses should contain a list of masses. In case the masses argument is not given or for those elements of the masses list that are None, standard values are set.

set_momenta(momenta, apply_constraint=True)

Set momenta.

set_pbc(pbc)

Set periodic boundary condition flags.

set_positions(newpositions, apply_constraint=True)

Set positions, honoring any constraints. To ignore constraints, use apply_constraint=False.

set_scaled_positions(scaled)

Set positions relative to unit cell.

set_tags(tags)

Set tags for all atoms. If only one tag is supplied, it is applied to all atoms.

set_velocities(velocities)

Set the momenta by specifying the velocities.

property symbols

Get chemical symbols as a ase.symbols.Symbols object.

The object works like atoms.numbers except its values are strings. It supports in-place editing.

todict()

For basic JSON (non-database) support.

translate(displacement)

Translate atomic positions.

The displacement argument can be a float an xyz vector or an nx3 array (where n is the number of atoms).

wrap(**wrap_kw)

Wrap positions to unit cell.

Parameters:

wrap_kw: (keyword=value) pairs

optional keywords \(pbc\), \(center\), \(pretty_translation\), \(eps\), see ase.geometry.wrap_positions()

write(filename, format=None, **kwargs)

Write atoms object to a file.

see ase.io.write for formats. kwargs are passed to ase.io.write.