Ring of polynomials over another ring. More...

#include <polynomi.h>

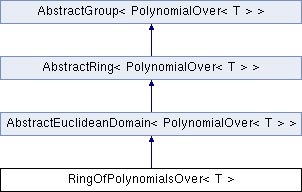
Inheritance diagram for RingOfPolynomialsOver< T >:

Classes
class	InterpolationFailed

Public Types
typedef T	CoefficientRing

typedef PolynomialOver< T >	Element

typedef Element::CoefficientType	CoefficientType

typedef Element::RandomizationParameter	RandomizationParameter

Public Types inherited from AbstractEuclideanDomain< PolynomialOver< T > >
typedef PolynomialOver< T >	Element

Public Types inherited from AbstractRing< PolynomialOver< T > >
typedef PolynomialOver< T >	Element

Public Types inherited from AbstractGroup< PolynomialOver< T > >
typedef PolynomialOver< T >	Element

Public Member Functions
	RingOfPolynomialsOver (const CoefficientRing &ring)

Element	RandomElement (RandomNumberGenerator &rng, const RandomizationParameter &parameter)

bool	Equal (const Element &a, const Element &b) const
	Compare two elements for equality. More...

const Element &	Identity () const
	Provides the Identity element. More...

const Element &	Add (const Element &a, const Element &b) const
	Adds elements in the group. More...

Element &	Accumulate (Element &a, const Element &b) const
	TODO. More...

const Element &	Inverse (const Element &a) const
	Inverts the element in the group. More...

const Element &	Subtract (const Element &a, const Element &b) const
	Subtracts elements in the group. More...

Element &	Reduce (Element &a, const Element &b) const
	Reduces an element in the congruence class. More...

const Element &	Double (const Element &a) const
	Doubles an element in the group. More...

const Element &	MultiplicativeIdentity () const
	Retrieves the multiplicative identity. More...

const Element &	Multiply (const Element &a, const Element &b) const
	Multiplies elements in the group. More...

const Element &	Square (const Element &a) const
	Square an element in the group. More...

bool	IsUnit (const Element &a) const
	Determines whether an element is a unit in the group. More...

const Element &	MultiplicativeInverse (const Element &a) const
	Calculate the multiplicative inverse of an element in the group. More...

const Element &	Divide (const Element &a, const Element &b) const
	Divides elements in the group. More...

const Element &	Mod (const Element &a, const Element &b) const
	Performs a modular reduction in the ring. More...

void	DivisionAlgorithm (Element &r, Element &q, const Element &a, const Element &d) const
	Performs the division algorithm on two elements in the ring. More...

Element	Interpolate (const CoefficientType x[], const CoefficientType y[], unsigned int n) const

CoefficientType	InterpolateAt (const CoefficientType &position, const CoefficientType x[], const CoefficientType y[], unsigned int n) const

Public Member Functions inherited from AbstractEuclideanDomain< PolynomialOver< T > >
virtual void	DivisionAlgorithm (Element &r, Element &q, const Element &a, const Element &d) const=0
	Performs the division algorithm on two elements in the ring. More...

virtual const Element &	Mod (const Element &a, const Element &b) const=0
	Performs a modular reduction in the ring. More...

virtual const Element &	Gcd (const Element &a, const Element &b) const
	Calculates the greatest common denominator in the ring. More...

Public Member Functions inherited from AbstractRing< PolynomialOver< T > >
	AbstractRing ()
	Construct an AbstractRing. More...

	AbstractRing (const AbstractRing &source)
	Copy construct an AbstractRing. More...

AbstractRing &	operator= (const AbstractRing &source)
	Assign an AbstractRing. More...

virtual bool	IsUnit (const Element &a) const=0
	Determines whether an element is a unit in the group. More...

virtual const Element &	MultiplicativeIdentity () const=0
	Retrieves the multiplicative identity. More...

virtual const Element &	Multiply (const Element &a, const Element &b) const=0
	Multiplies elements in the group. More...

virtual const Element &	MultiplicativeInverse (const Element &a) const=0
	Calculate the multiplicative inverse of an element in the group. More...

virtual const Element &	Square (const Element &a) const
	Square an element in the group. More...

virtual const Element &	Divide (const Element &a, const Element &b) const
	Divides elements in the group. More...

virtual Element	Exponentiate (const Element &a, const Integer &e) const
	Raises a base to an exponent in the group. More...

virtual Element	CascadeExponentiate (const Element &x, const Integer &e1, const Element &y, const Integer &e2) const
	TODO. More...

virtual void	SimultaneousExponentiate (Element results, const Element &base, const Integer exponents, unsigned int exponentsCount) const
	Exponentiates a base to multiple exponents in the Ring. More...

virtual const AbstractGroup< PolynomialOver< T > > &	MultiplicativeGroup () const
	Retrieves the multiplicative group. More...

Public Member Functions inherited from AbstractGroup< PolynomialOver< T > >
virtual bool	Equal (const Element &a, const Element &b) const=0
	Compare two elements for equality. More...

virtual const Element &	Identity () const=0
	Provides the Identity element. More...

virtual const Element &	Add (const Element &a, const Element &b) const=0
	Adds elements in the group. More...

virtual const Element &	Inverse (const Element &a) const=0
	Inverts the element in the group. More...

virtual bool	InversionIsFast () const
	Determine if inversion is fast. More...

virtual const Element &	Double (const Element &a) const
	Doubles an element in the group. More...

virtual const Element &	Subtract (const Element &a, const Element &b) const
	Subtracts elements in the group. More...

virtual Element &	Accumulate (Element &a, const Element &b) const
	TODO. More...

virtual Element &	Reduce (Element &a, const Element &b) const
	Reduces an element in the congruence class. More...

virtual Element	ScalarMultiply (const Element &a, const Integer &e) const
	Performs a scalar multiplication. More...

virtual Element	CascadeScalarMultiply (const Element &x, const Integer &e1, const Element &y, const Integer &e2) const
	TODO. More...

virtual void	SimultaneousMultiply (Element results, const Element &base, const Integer exponents, unsigned int exponentsCount) const
	Multiplies a base to multiple exponents in a group. More...

Detailed Description

template<class T>
class RingOfPolynomialsOver< T >

Ring of polynomials over another ring.

Definition at line 314 of file polynomi.h.

Member Typedef Documentation

◆ CoefficientRing

template<class T >

typedef T RingOfPolynomialsOver< T >::CoefficientRing

Definition at line 317 of file polynomi.h.

◆ Element

template<class T >

typedef PolynomialOver<T> RingOfPolynomialsOver< T >::Element

Definition at line 318 of file polynomi.h.

◆ CoefficientType

template<class T >

typedef Element::CoefficientType RingOfPolynomialsOver< T >::CoefficientType

Definition at line 319 of file polynomi.h.

◆ RandomizationParameter

template<class T >

typedef Element::RandomizationParameter RingOfPolynomialsOver< T >::RandomizationParameter

Definition at line 320 of file polynomi.h.

Constructor & Destructor Documentation

◆ RingOfPolynomialsOver()

template<class T >

RingOfPolynomialsOver< T >::RingOfPolynomialsOver ( const CoefficientRing & ring )

inline

Definition at line 322 of file polynomi.h.

Member Function Documentation

◆ RandomElement()

template<class T >

Element RingOfPolynomialsOver< T >::RandomElement	(	RandomNumberGenerator &	rng,
		const RandomizationParameter &	parameter
	)

inline

Definition at line 324 of file polynomi.h.

◆ Equal()

template<class T >

bool RingOfPolynomialsOver< T >::Equal	(	const Element &	a,
		const Element &	b
	)		const

inlinevirtual

Compare two elements for equality.

Parameters

a	first element
b	second element

Returns: true if the elements are equal, false otherwise

Equal() tests the elements for equality using a==b

Implements AbstractGroup< PolynomialOver< T > >.

Definition at line 327 of file polynomi.h.

◆ Identity()

template<class T >

const Element & RingOfPolynomialsOver< T >::Identity ( ) const

inlinevirtual

Provides the Identity element.

Returns: the Identity element

Implements AbstractGroup< PolynomialOver< T > >.

Definition at line 330 of file polynomi.h.

◆ Add()

template<class T >

const Element & RingOfPolynomialsOver< T >::Add	(	const Element &	a,
		const Element &	b
	)		const

inlinevirtual

Adds elements in the group.

Parameters

a	first element
b	second element

Returns: the sum of a and b

Implements AbstractGroup< PolynomialOver< T > >.

Definition at line 333 of file polynomi.h.

◆ Accumulate()

template<class T >

Element & RingOfPolynomialsOver< T >::Accumulate	(	Element &	a,
		const Element &	b
	)		const

inlinevirtual

TODO.

Parameters

a	first element
b	second element

Returns: TODO

Reimplemented from AbstractGroup< PolynomialOver< T > >.

Definition at line 336 of file polynomi.h.

◆ Inverse()

template<class T >

const Element & RingOfPolynomialsOver< T >::Inverse ( const Element & a ) const

inlinevirtual

Inverts the element in the group.

Parameters

a	first element

Returns: the inverse of the element

Implements AbstractGroup< PolynomialOver< T > >.

Definition at line 339 of file polynomi.h.

◆ Subtract()

template<class T >

const Element & RingOfPolynomialsOver< T >::Subtract	(	const Element &	a,
		const Element &	b
	)		const

inlinevirtual

Subtracts elements in the group.

Parameters

a	first element
b	second element

Returns: the difference of a and b. The element a must provide a Subtract member function.

Reimplemented from AbstractGroup< PolynomialOver< T > >.

Definition at line 342 of file polynomi.h.

◆ Reduce()

template<class T >

Element & RingOfPolynomialsOver< T >::Reduce	(	Element &	a,
		const Element &	b
	)		const

inlinevirtual

Reduces an element in the congruence class.

Parameters

a	element to reduce
b	the congruence class

Returns: the reduced element

Reimplemented from AbstractGroup< PolynomialOver< T > >.

Definition at line 345 of file polynomi.h.

◆ Double()

template<class T >

const Element & RingOfPolynomialsOver< T >::Double ( const Element & a ) const

inlinevirtual

Doubles an element in the group.

Parameters

a	the element

Returns: the element doubled

Reimplemented from AbstractGroup< PolynomialOver< T > >.

Definition at line 348 of file polynomi.h.

◆ MultiplicativeIdentity()

template<class T >

const Element & RingOfPolynomialsOver< T >::MultiplicativeIdentity ( ) const

inlinevirtual

Retrieves the multiplicative identity.

Returns: the multiplicative identity

Implements AbstractRing< PolynomialOver< T > >.

Definition at line 351 of file polynomi.h.

◆ Multiply()

template<class T >

const Element & RingOfPolynomialsOver< T >::Multiply	(	const Element &	a,
		const Element &	b
	)		const

inlinevirtual

Multiplies elements in the group.

Parameters

a	the multiplicand
b	the multiplier

Returns: the product of a and b

Implements AbstractRing< PolynomialOver< T > >.

Definition at line 354 of file polynomi.h.

◆ Square()

template<class T >

const Element & RingOfPolynomialsOver< T >::Square ( const Element & a ) const

inlinevirtual

Square an element in the group.

Parameters

a	the element

Returns: the element squared

Reimplemented from AbstractRing< PolynomialOver< T > >.

Definition at line 357 of file polynomi.h.

◆ IsUnit()

template<class T >

bool RingOfPolynomialsOver< T >::IsUnit ( const Element & a ) const

inlinevirtual

Determines whether an element is a unit in the group.

Parameters

a	the element

Returns: true if the element is a unit after reduction, false otherwise.

Implements AbstractRing< PolynomialOver< T > >.

Definition at line 360 of file polynomi.h.

◆ MultiplicativeInverse()

template<class T >

const Element & RingOfPolynomialsOver< T >::MultiplicativeInverse ( const Element & a ) const

inlinevirtual

Calculate the multiplicative inverse of an element in the group.

Parameters

a	the element

Implements AbstractRing< PolynomialOver< T > >.

Definition at line 363 of file polynomi.h.

◆ Divide()

template<class T >

const Element & RingOfPolynomialsOver< T >::Divide	(	const Element &	a,
		const Element &	b
	)		const

inlinevirtual

Divides elements in the group.

Parameters

a	the dividend
b	the divisor

Returns: the quotient

Reimplemented from AbstractRing< PolynomialOver< T > >.

Definition at line 366 of file polynomi.h.

◆ Mod()

template<class T >

const Element & RingOfPolynomialsOver< T >::Mod	(	const Element &	a,
		const Element &	b
	)		const

inlinevirtual

Performs a modular reduction in the ring.

Parameters

a	the element
b	the modulus

Returns: the result of ab.

Implements AbstractEuclideanDomain< PolynomialOver< T > >.

Definition at line 369 of file polynomi.h.

◆ DivisionAlgorithm()

template<class T >

void RingOfPolynomialsOver< T >::DivisionAlgorithm	(	Element &	r,
		Element &	q,
		const Element &	a,
		const Element &	d
	)		const

inlinevirtual

Performs the division algorithm on two elements in the ring.

Parameters

r	the remainder
q	the quotient
a	the dividend
d	the divisor

Implements AbstractEuclideanDomain< PolynomialOver< T > >.

Definition at line 372 of file polynomi.h.

◆ Interpolate()

template<class T >

RingOfPolynomialsOver< T >::Element RingOfPolynomialsOver< T >::Interpolate	(	const CoefficientType	x[],
		const CoefficientType	y[],
		unsigned int	n
	)		const

Definition at line 476 of file polynomi.cpp.

◆ InterpolateAt()

template<class T >

RingOfPolynomialsOver< T >::CoefficientType RingOfPolynomialsOver< T >::InterpolateAt	(	const CoefficientType &	position,
		const CoefficientType	x[],
		const CoefficientType	y[],
		unsigned int	n
	)		const

Definition at line 498 of file polynomi.cpp.

The documentation for this class was generated from the following files:

Classes

Public Types

Public Member Functions

Detailed Description

Member Typedef Documentation

◆ CoefficientRing

◆ Element

◆ CoefficientType

◆ RandomizationParameter

Constructor & Destructor Documentation

◆ RingOfPolynomialsOver()

Member Function Documentation

◆ RandomElement()

◆ Equal()

◆ Identity()

◆ Add()

◆ Accumulate()

◆ Inverse()

◆ Subtract()

◆ Reduce()

◆ Double()

◆ MultiplicativeIdentity()

◆ Multiply()

◆ Square()

◆ IsUnit()

◆ MultiplicativeInverse()

◆ Divide()

◆ Mod()

◆ DivisionAlgorithm()

◆ Interpolate()

◆ InterpolateAt()