v.generalize - GRASS GIS manual

NAME

v.generalize - Performs vector based generalization.

KEYWORDS

vector, generalization, simplification, smoothing, displacement, network generalization, topology, geometry

SYNOPSIS

v.generalize

v.generalize --help

v.generalize [-lt] input=name [layer=string] [type=string[,string,...]] output=name [error=name] method=string threshold=float [look_ahead=integer] [reduction=float] [slide=float] [angle_thresh=float] [degree_thresh=integer] [closeness_thresh=float] [betweeness_thresh=float] [alpha=float] [beta=float] [iterations=integer] [cats=range] [where=sql_query] [--overwrite] [--help] [--verbose] [--quiet] [--ui]

Flags:

-l: Disable loop support; Do not modify end points of lines forming a closed loop
-t: Do not copy attributes
--overwrite: Allow output files to overwrite existing files
--help: Print usage summary
--verbose: Verbose module output
--quiet: Quiet module output
--ui: Force launching GUI dialog

Parameters:

input=name [required]: Name of input vector map; Or data source for direct OGR access
layer=string: Layer number or name ('-1' for all layers); A single vector map can be connected to multiple database tables. This number determines which table to use. When used with direct OGR access this is the layer name.; Default: -1
type=string[,string,...]: Input feature type; Options: line, boundary, area; Default: line,boundary,area
output=name [required]: Name for output vector map
error=name: Error map with failed generalizations; Lines and boundaries causing errors (collapsed to a point or topology errors)
method=string [required]: Generalization algorithm; Options: douglas, douglas_reduction, lang, reduction, reumann, boyle, sliding_averaging, distance_weighting, chaiken, hermite, snakes, network, displacement; douglas: Douglas-Peucker Algorithm; douglas_reduction: Douglas-Peucker Algorithm with reduction parameter; lang: Lang Simplification Algorithm; reduction: Vertex Reduction Algorithm eliminates points close to each other; reumann: Reumann-Witkam Algorithm; boyle: Boyle's Forward-Looking Algorithm; sliding_averaging: McMaster's Sliding Averaging Algorithm; distance_weighting: McMaster's Distance-Weighting Algorithm; chaiken: Chaiken's Algorithm; hermite: Interpolation by Cubic Hermite Splines; snakes: Snakes method for line smoothing; network: Network generalization; displacement: Displacement of lines close to each other
threshold=float [required]: Maximal tolerance value; Options: 0-1000000000
look_ahead=integer: Look-ahead parameter; Default: 7
reduction=float: Percentage of the points in the output of 'douglas_reduction' algorithm; Options: 0-100; Default: 50
slide=float: Slide of computed point toward the original point; Options: 0-1; Default: 0.5
angle_thresh=float: Minimum angle between two consecutive segments in Hermite method; Options: 0-180; Default: 3
degree_thresh=integer: Degree threshold in network generalization; Default: 0
closeness_thresh=float: Closeness threshold in network generalization; Options: 0-1; Default: 0
betweeness_thresh=float: Betweeness threshold in network generalization; Default: 0
alpha=float: Snakes alpha parameter; Default: 1.0
beta=float: Snakes beta parameter; Default: 1.0
iterations=integer: Number of iterations; Default: 1
cats=range: Category values; Example: 1,3,7-9,13
where=sql_query: WHERE conditions of SQL statement without 'where' keyword; Example: income < 1000 and population >= 10000

DESCRIPTION
NOTES
EXAMPLES
- SIMPLIFICATION EXAMPLE
- SMOOTHING EXAMPLE
SEE ALSO
AUTHORS

DESCRIPTION

v.generalize is a module for the generalization of GRASS vector maps. This module consists of algorithms for line simplification, line smoothing, network generalization and displacement (new methods may be added later).

The cats and where options are used only if a layer > 0 is specified, otherwise, those options are ignored. Be aware that the default is layer=-1, meaning that all layers are processed, ignoring the cats and where options.

If type=area is selected, boundaries of selected areas will be generalized, and the options cats, where, and layer will be used to select areas.

NOTES

(Line) simplification is a process of reducing the complexity of vector features. The module transforms a line into another line consisting of fewer vertices, that still approximate the original line. Most of the algorithms described below select a subset of points on the original line.

(Line) smoothing is a "reverse" process which takes as input a line and produces a smoother approximate of the original. In some cases, this is achieved by inserting new vertices into the original line, and can total up to 4000% of the number of vertices in the original. In such an instance, it is always a good idea to simplify the line after smoothing.

Smoothing and simplification algorithms implemented in this module work line by line, i.e. simplification/smoothing of one line does not affect the other lines; they are treated separately. For isolated loops formed by a single line/boundary, he first and the last point of each line/boundary can be translated and/or deleted, unless the -l flag is used to disable loop support.

Lines and boundaries are not translated if they would collapse to a single point. Boundaries are not translated if they would intersect with themselves or other boundaries. Such erroneous features are written to an optional error vector map. Overlaying the error map over the generalized map indicates the kind of error. Lines/boundaries collapsing to a point are written out as points, boundaries violating topology are written out as boundaries. The error map can be overlaid over the generalized map to understand why some features were not generalized.

SIMPLIFICATION

Simplification can fail for many boundaries if the simplification parameters would result in a large reduction of vertices. If many lines/boundaries could not be simplified, try different parameters that would cause a lower degree of simplification.

v.generalize contains following line simplification algorithms:

Douglas-Peucker Algorithm
Douglas-Peucker Reduction Algorithm
Lang Algorithm
Vertex Reduction
Reumann-Witkam Algorithm

Different algorithms require different parameters, but all the algorithms have one parameter in common: the threshold parameter, given in map units (for latitude-longitude locations: in decimal degree). In general, the degree of simplification increases with the increasing value of threshold.

ALGORITHM DESCRIPTIONS

Douglas-Peucker - "Quicksort" of line simplification, the most widely used algorithm. Input parameters: input, threshold. For more information, see:
http://geomalgorithms.com/a16-_decimate-1.html.
Douglas-Peucker Reduction Algorithm is essentially the same algorithm as the algorithm above, the difference being that it takes an additional reduction parameter which denotes the percentage of the number of points on the new line with respect to the number of points on the original line. Input parameters: input, threshold, reduction.
Lang - Another standard algorithm. Input parameters: input, threshold, look_ahead. For an excellent description, see:
http://www.sli.unimelb.edu.au/gisweb/LGmodule/LGLangVisualisation.htm.
Vertex Reduction - Simplest among the algorithms. Input parameters: input, threshold. Given a line, this algorithm removes the points of this line which are closer to each other than threshold. More precisely, if p1 and p2 are two consecutive points, and the distance between p2 and p1 is less than threshold, it removes p2 and repeats the same process on the remaining points.
Reumann-Witkam - Input parameters: input, threshold. This algorithm quite reasonably preserves the global characteristics of the lines. For more information, see for example:
http://psimpl.sourceforge.net/reumann-witkam.html.

Douglas-Peucker and Douglas-Peucker Reduction Algorithm use the same method to simplify the lines. Note that

v.generalize input=boundary_county output=boundary_county_dp20 method=douglas threshold=20

is equivalent to

v.generalize input=boundary_county output=boundary_county_dp_red20_100 \
             method=douglas_reduction threshold=20 reduction=100

However, in this case, the first method is faster. Also observe that douglas_reduction never outputs more vertices than douglas, and that, in general, douglas is more efficient than douglas_reduction. More importantly, the effect of

v.generalize input=boundary_county output=boundary_county_dp_red0_30 \
             method=douglas_reduction threshold=0 reduction=30

is that 'out' contains approximately only 30% of points of 'in'.

SMOOTHING

The following smoothing algorithms are implemented in v.generalize:

Boyle's Forward-Looking Algorithm - The position of each point depends on the position of the previous points and the point look_ahead ahead. look_ahead consecutive points. Input parameters: input, look_ahead.
McMaster's Sliding Averaging Algorithm - Input Parameters: input, slide, look_ahead. The new position of each point is the average of the look_ahead points around. Parameter slide is used for linear interpolation between old and new position (see below).
McMaster's Distance-Weighting Algorithm - Takes the weighted average of look_ahead consecutive points where the weight is the reciprocal of the distance from the point to the currently smoothed point. The parameter slide is used for linear interpolation between the original position of the point and newly computed position where value 0 means the original position. Input parameters: input, slide, look_ahead.
Chaiken's Algorithm - "Inscribes" a line touching the original line such that the points on this new line are at least threshold apart. Input parameters: input, threshold. This algorithm approximates the given line very well.
Hermite Interpolation - This algorithm takes the points of the given line as the control points of hermite cubic spline and approximates this spline by the points approximately threshold apart. This method has excellent results for small values of threshold, but in this case it produces a huge number of new points and some simplification is usually needed. Input parameters: input, threshold, angle_thresh. Angle_thresh is used for reducing the number of the points. It denotes the minimal angle (in degrees) between two consecutive segments of a line.
Snakes is the method of minimisation of the "energy" of a line. This method preserves the general characteristics of the lines but smooths the "sharp corners" of a line. Input parameters input, alpha, beta. This algorithm works very well for small values of alpha and beta (between 0 and 5). These parameters affect the "sharpness" and the curvature of the computed line.

One of the key advantages of Hermite Interpolation is the fact that the computed line always passes through the points of the original line, whereas the lines produced by the remaining algorithms never pass through these points. In some sense, this algorithm outputs a line which "circumscribes" the input line.

On the other hand, Chaiken's Algorithm outputs a line which "inscribes" a given line. The output line always touches/intersects the centre of the input line segment between two consecutive points. For more iterations, the property above does not hold, but the computed lines are very similar to the Bezier Splines. The disadvantage of the two algorithms given above is that they increase the number of points. However, Hermite Interpolation can be used as another simplification algorithm. To achieve this, it is necessary to set angle_thresh to higher values (15 or so).

One restriction on both McMasters' Algorithms is that look_ahead parameter must be odd. Also note that these algorithms have no effect if look_ahead = 1.

Note that Boyle's, McMasters' and Snakes algorithm are sometimes used in the signal processing to smooth the signals. More importantly, these algorithms never change the number of points on the lines; they only translate the points, and do not insert any new points.

Snakes Algorithm is (asymptotically) the slowest among the algorithms presented above. Also, it requires quite a lot of memory. This means that it is not very efficient for maps with the lines consisting of many segments.

DISPLACEMENT

The displacement is used when the lines overlap and/or are close to each other at the current level of detail. In general, displacement methods move the conflicting features apart so that they do not interact and can be distinguished.

This module implements an algorithm for displacement of linear features based on the Snakes approach. This method generally yields very good results; however, it requires a lot of memory and is not very efficient.

Displacement is selected by method=displacement. It uses the following parameters:

threshold - specifies critical distance. Two features interact if they are closer than threshold apart.
alpha, beta - These parameters define the rigidity of lines. For larger values of alpha, beta (>=1), the algorithm does a better job at retaining the original shape of the lines, possibly at the expense of displacement distance. If the values of alpha, beta are too small (<=0.001), then the lines are moved sufficiently, but the geometry and topology of lines can be destroyed. Most likely the best way to find the good values of alpha, beta is by trial and error.
iterations - denotes the number of iterations the interactions between the lines are resolved. Good starting points for values of iterations are between 10 and 100.

The lines affected by the algorithm can be specified by the layer, cats and where parameters.

NETWORK GENERALIZATION

Used for selecting "the most important" part of the network. This is based on the graph algorithms. Network generalization is applied if method=network. The algorithm calculates three centrality measures for each line in the network and only the lines with the values greater than thresholds are selected. The behaviour of algorithm can be altered by the following parameters:

degree_thresh - algorithm selects only the lines which share a point with at least degree_thresh different lines.
closeness_thresh - is always in the range (0, 1]. Only the lines with the closeness centrality value at least closeness_thresh apart are selected. The lines in the centre of a network have greater values of this measure than the lines near the border of a network. This means that this parameter can be used for selecting the centre(s) of a network. Note that if closeness_thresh=0 then everything is selected.
betweeness_thresh - Again, only the lines with a betweeness centrality measure at least betweeness_thresh are selected. This value is always positive and is larger for large networks. It denotes to what extent a line is in between the other lines in the network. This value is large for the lines which lie between other lines and lie on the paths between two parts of a network. In the terminology of road networks, these are highways, bypasses, main roads/streets, etc.

All three parameters above can be presented at the same time. In that case, the algorithm selects only the lines which meet each criterion.

Also, the outputed network may not be connected if the value of betweeness_thresh is too large.

EXAMPLES

SIMPLIFICATION EXAMPLE

Simplification of county boundaries with DP method (North Carolina sample dataset), threshold given in mapset units (here: meters):

v.generalize input=boundary_county output=boundary_county_dp20 \
  method=douglas threshold=20 error=boundary_county_dp20_leftover

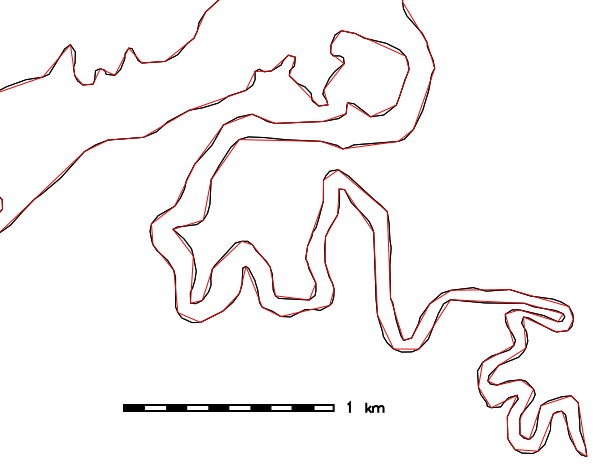
Figure: Vector simplification example (spatial subset: original map shown in black, simplified map with 26% remaining vertices shown in red)

SMOOTHING EXAMPLE

Smoothing of road network with Chaiken method (North Carolina sample dataset), threshold given in mapset units (here: meters):

v.generalize input=roads output=roads_chaiken method=chaiken \
  threshold=1 error=roads_chaiken_leftover

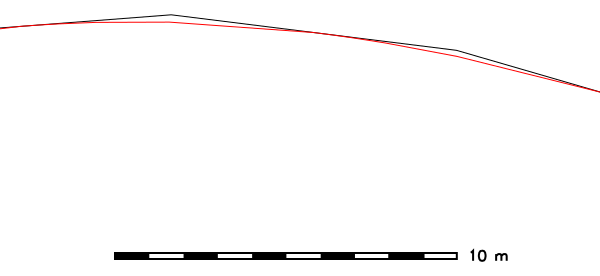
Figure: Vector smoothing example (spatial subset: original map shown in black, smoothed map with 500% increased number of vertices shown in red)

AUTHORS

Daniel Bundala, Google Summer of Code 2007, Student
Wolf Bergenheim, Mentor
Partial rewrite: Markus Metz

SOURCE CODE

Available at: v.generalize source code (history)

Accessed: Sunday Jan 22 07:37:01 2023