
NAME
r.horizon - Computes horizon angle height from a digital elevation model.The module has two different modes of operation: 1. Computes the entire horizon around a single point whose coordinates are given with the 'coord' option. The horizon height (in radians). 2. Computes one or more raster maps of the horizon height in a single direction. The input for this is the angle (in degrees), which is measured counterclockwise with east=0, north=90 etc. The output is the horizon height in radians.
KEYWORDS
raster, solar, sun positionSYNOPSIS
Flags:
- -d
- Write output in degrees (default is radians)
- -c
- Write output in compass orientation (default is CCW, East=0)
- --overwrite
- Allow output files to overwrite existing files
- --help
- Print usage summary
- --verbose
- Verbose module output
- --quiet
- Quiet module output
- --ui
- Force launching GUI dialog
Parameters:
- elevation=name [required]
- Name of input elevation raster map
- direction=float
- Direction in which you want to know the horizon height
- step=float
- Angle step size for multidirectional horizon [degrees]
- start=float
- Start angle for multidirectional horizon [degrees]
- Default: 0.0
- end=float
- End angle for multidirectional horizon [degrees]
- Default: 360.0
- bufferzone=float
- For horizon rasters, read from the DEM an extra buffer around the present region
- e_buff=float
- For horizon rasters, read from the DEM an extra buffer eastward the present region
- w_buff=float
- For horizon rasters, read from the DEM an extra buffer westward the present region
- n_buff=float
- For horizon rasters, read from the DEM an extra buffer northward the present region
- s_buff=float
- For horizon rasters, read from the DEM an extra buffer southward the present region
- maxdistance=float
- The maximum distance to consider when finding the horizon height
- output=basename
- Name for output basename raster map(s)
- coordinates=east,north
- Coordinate for which you want to calculate the horizon
- distance=float
- Sampling distance step coefficient (0.5-1.5)
- Default: 1.0
- file=name
- Name of file for output (use output=- for stdout)
- Default: -
Table of contents
DESCRIPTION
r.horizon computes the angular height of terrain horizon in radians. It reads a raster of elevation data and outputs the horizon outline in one of two modes:- single point: as a series of horizon heights in the specified directions from the given point. The results are written to the stdout.
- raster: in this case the output is one or more raster maps, with each point in a raster giving the horizon height in a specific direction. One raster is created for each direction.
The directions are given as azimuthal angles (in degrees), with the angle starting with 0 towards East and moving counterclockwise (North is 90, etc.). The calculation takes into account the actual projection, so the angles are corrected for direction distortions imposed by it. The directions are thus aligned to those of the geographic projection and not the coordinate system given by the rows and columns of the raster map. This correction implies that the resulting cardinal directions represent true orientation towards the East, North, West and South. The only exception of this feature is LOCATION with x,y coordinate system, where this correction is not applied.
Using the -c flag, the azimuthal angles will be printed in compass orientation (North=0, clockwise).
Input parameters:
The elevation parameter is an input elevation raster map. If the buffer options are used (see below), this raster should extend over the area that accommodate the presently defined region plus defined buffer zones.
The step parameter gives the angle step (in degrees) between successive azimuthal directions for the calculation of the horizon. Thus, a value of 5 for the step will give a total of 360/5=72 directions (72 raster maps if used in the raster map mode).
The start parameter gives the angle start (in degrees) for the calculation of the horizon. The default value is 0 (East with North being 90 etc.).
The end parameter gives the angle end (in degrees) for the calculation of the horizon. The end point is omitted! So for example if we run r.horizon with step=10, start=30 and end=70 the raster maps generated by r.horizon will be only for angles: 30, 40, 50, 60. The default value is 360.
The direction parameter gives the initial direction of the first output. This parameter acts as an direction angle offset. For example, if you want to get horizon angles for directions 45 and 225 degrees, the direction should be set to 45 and step to 180. If you only want one single direction, use this parameter to specify desired direction of horizon angle, and set the step size to 0 degrees. Otherwise all angles for a given starting direction with step of step are calculated.
The distance controls the sampling distance step size for the search for horizon along the line of sight. The default value is 1.0 meaning that the step size will be taken from the raster resolution. Setting the value below 1.0 might slightly improve results for directions apart from the cardinal ones, but increasing the processing load of the search algorithm.
The maxdistance value gives a maximum distance to move away from the origin along the line of sight in order to search for the horizon height. The default maxdistance is the full map extent. The smaller this value the faster the calculation but the higher the risk that you may miss a terrain feature that can contribute significantly to the horizon outline. Note that a viewshed can be calculated with r.viewshed.
The coordinate parameter takes a pair of easting-northing values in the current coordinate system and calculates the values of angular height of the horizon around this point. To achieve the consistency of the results, the point coordinate is aligned to the midpoint of the closest elevation raster cell.
If an analyzed point (or raster cell) lies close to the edge of the defined region, the horizon calculation may not be realistic, since it may not see some significant terrain features which could have contributed to the horizon, because these features are outside the region. There are to options how to set the size of the buffer that is used to increase the area of the horizon analysis. The bufferzone parameter allows you to specify the same size of buffer for all cardinal directions and the parameters e_buff, n_buff, s_buff, and w_buff allow you to specify a buffer size individually for each of the four directions. The buffer parameters influence only size of the read elevation map, while the analysis in the raster mode will be done only for the area specified by the current region definition.
The output parameter defines the basename of the output horizon raster maps. The raster name of each horizon direction raster will be constructed as basename_ANGLE, where ANGLE is the angle in degrees with the direction. If you use r.horizon in the single point mode this option will be ignored.
The file parameter allows saving the resulting horizon angles in a comma separated ASCII file (single point mode only). If you use r.horizon in the raster map mode this option will be ignored.
At the moment the elevation and maximum distance must be measured in meters, even if you use geographical coordinates (longitude/latitude). If your projection is based on distance (easting and northing), these too must be in meters. The buffer parameters must be in the same units as the raster coordinates (e.g., for latitude-longitude locations buffers are measured in degree unit).
METHOD
The calculation method is based on the method used in r.sun to calculate shadows. It starts at a very shallow angle and walks along the line of sight and asks at each step whether the line of sight "hits" the terrain. If so, the angle is increased to allow the line of sight to pass just above the terrain at that point. This is continued until the line of sight reaches a height that is higher than any point in the region or until it reaches the border of the region (see also the bufferzone,e_buff, n_buff, s_buff, and w_buff). The the number of lines of sight (azimuth directions) is determined from the direction and step parameters. The method takes into account the curvature of the Earth whereby remote features will seem to be lower than they actually are. It also accounts for the changes of angles towards cardinal directions caused by the projection (see above).The output with the -d flag is azimuth degree (-90 to 90, where 0 is parallel with the focal cell). In case of negative horizon values obtained this indicates that the horizon height is below the cell it is computed from.
EXAMPLES
The examples are intended for the North Carolina sample dataset.Single point mode
Example 1: determine horizon angle in 225 degree direction (output of horizon angles CCW from East):g.region raster=elevation -p
r.horizon elevation=elevation direction=215 step=0 bufferzone=200 \
coordinates=638871.6,223384.4 maxdistance=5000
Example 2: determine horizon values starting at 90 deg (North), step size of 5 deg, saving result as CSV file:
r.horizon elevation=elevation direction=90 step=5 bufferzone=200 \
coordinates=638871.6,223384.4 maxdistance=5000 file=horizon.csv
Example 3: test point near highway intersection, saving result as CSV file for plotting the horizon around the highway intersection:
g.region n=223540 s=220820 w=634650 e=638780 res=10 -p
r.horizon elevation=elevation direction=0 step=5 bufferzone=200 \
coordinates=636483.54,222176.25 maxdistance=5000 -d file=horizon.csv

Test point near high way intersection (North Carolina sample dataset)
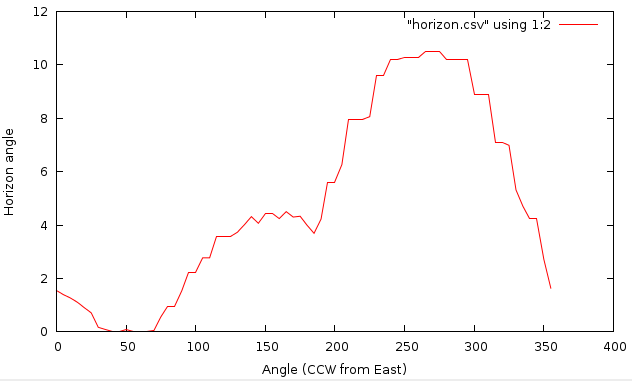
Horizon angles for test point (CCW from East)
We can plot horizon in polar coordinates using Matplotlib in Python:
import numpy as np
import matplotlib.pyplot as plt
horizon = np.genfromtxt('horizon.csv', delimiter=',')
horizon = horizon[1:, :]
ax = plt.subplot(111, polar=True)
bars = ax.plot(horizon[:, 0] / 180 * np.pi,
(90 - horizon[:, 1]) / 180 * np.pi)
# uncomment the 2 following lines when using -c flag
# ax.set_theta_direction(-1)
# ax.set_theta_zero_location('N')
plt.show()
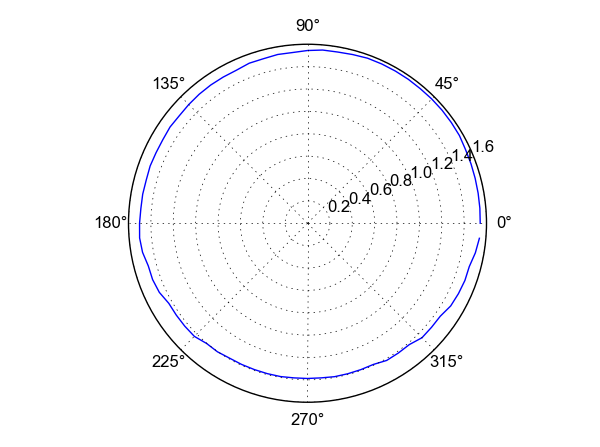
Horizon plot in polar coordinates.
Raster map mode
Raster map mode (output maps "horangle*" become input for r.sun):g.region raster=elevation -p
# we put a bufferzone of 10% of maxdistance around the study area
# compute only direction between 90 and 270 degrees
r.horizon elevation=elevation step=30 start=90 end=300 \
bufferzone=200 output=horangle maxdistance=5000
REFERENCES
Hofierka J., 1997. Direct solar radiation modelling within an open GIS environment. Proceedings of JEC-GI'97 conference in Vienna, Austria, IOS Press Amsterdam, 575-584
Hofierka J., Huld T., Cebecauer T., Suri M., 2007. Open Source Solar Radiation Tools for Environmental and Renewable Energy Applications, International Symposium on Environmental Software Systems, Prague, 2007
Neteler M., Mitasova H., 2004. Open Source GIS: A GRASS GIS Approach, Springer, New York. ISBN: 1-4020-8064-6, 2nd Edition 2004 (reprinted 2005), 424 pages
Project PVGIS, European Commission, DG Joint Research Centre 2001-2007
Suri M., Hofierka J., 2004. A New GIS-based Solar Radiation Model and Its Application for Photovoltaic Assessments. Transactions in GIS, 8(2), 175-190
SEE ALSO
r.sun, r.sunmask, r.viewshedAUTHORS
Thomas Huld, Joint Research Centre of the European Commission, Ispra, ItalyTomas Cebecauer, Joint Research Centre
of the European Commission, Ispra, Italy
Jaroslav Hofierka, GeoModel s.r.o.,
Bratislava, Slovakia
Marcel Suri, Joint Research Centre of the
European Commission, Ispra, Italy
© 2007, Thomas Huld, Tomas Cebecauer, Jaroslav Hofierka, Marcel Suri Thomas.Huld@jrc.it Tomas.Cebecauer@jrc.it hofierka@geomodel.sk Marcel.Suri@jrc.it
SOURCE CODE
Available at: r.horizon source code (history)
Accessed: Sunday Jan 22 07:36:12 2023
Main index | Raster index | Topics index | Keywords index | Graphical index | Full index
© 2003-2023 GRASS Development Team, GRASS GIS 8.2.1 Reference Manual