Finite Field PACK Set of elimination based routines for dense linear algebra. More...

Data Structures
class	Failure
	A precondtion failed. More...

Functions
void	LAPACKPerm2MathPerm (size_t MathP, const size_t LapackP, const size_t N)
	Conversion of a permutation from LAPACK format to Math format.

void	MathPerm2LAPACKPerm (size_t LapackP, const size_t MathP, const size_t N)
	Conversion of a permutation from Maths format to LAPACK format.

template<class Field >
void	applyP (const Field &F, const FFLAS::FFLAS_SIDE Side, const FFLAS::FFLAS_TRANSPOSE Trans, const size_t M, const size_t ibeg, const size_t iend, typename Field::Element_ptr A, const size_t lda, const size_t *P)
	Computes P1 x Diag (I_R, P2) where P1 is a LAPACK and P2 a LAPACK permutation and store the result in P1 as a LAPACK permutation. More...

template<class Field >
void	MonotonicApplyP (const Field &F, const FFLAS::FFLAS_SIDE Side, const FFLAS::FFLAS_TRANSPOSE Trans, const size_t M, const size_t ibeg, const size_t iend, typename Field::Element_ptr A, const size_t lda, const size_t *P, const size_t R)
	Apply a R-monotonically increasing permutation P, to the matrix A. More...

template<class Field >
void	fgetrs (const Field &F, const FFLAS::FFLAS_SIDE Side, const size_t M, const size_t N, const size_t R, typename Field::Element_ptr A, const size_t lda, const size_t P, const size_t Q, typename Field::Element_ptr B, const size_t ldb, int *info)
	Solve the system or . More...

template<class Field >
Field::Element_ptr	fgetrs (const Field &F, const FFLAS::FFLAS_SIDE Side, const size_t M, const size_t N, const size_t NRHS, const size_t R, typename Field::Element_ptr A, const size_t lda, const size_t P, const size_t Q, typename Field::Element_ptr X, const size_t ldx, typename Field::ConstElement_ptr B, const size_t ldb, int *info)
	Solve the system A X = B or X A = B. More...

template<class Field >
size_t	fgesv (const Field &F, const FFLAS::FFLAS_SIDE Side, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, typename Field::Element_ptr B, const size_t ldb, int *info)
	Square system solver. More...

template<class Field >
size_t	fgesv (const Field &F, const FFLAS::FFLAS_SIDE Side, const size_t M, const size_t N, const size_t NRHS, typename Field::Element_ptr A, const size_t lda, typename Field::Element_ptr X, const size_t ldx, typename Field::ConstElement_ptr B, const size_t ldb, int *info)
	Rectangular system solver. More...

template<class Field >
void	ftrtri (const Field &F, const FFLAS::FFLAS_UPLO Uplo, const FFLAS::FFLAS_DIAG Diag, const size_t N, typename Field::Element_ptr A, const size_t lda, const size_t threshold=__FFLASFFPACK_FTRTRI_THRESHOLD)
	Compute the inverse of a triangular matrix. More...

template<class Field >
void	ftrtrm (const Field &F, const FFLAS::FFLAS_SIDE side, const FFLAS::FFLAS_DIAG diag, const size_t N, typename Field::Element_ptr A, const size_t lda)
	Compute the product of two triangular matrices of opposite shape. More...

template<class Field >
void	ftrstr (const Field &F, const FFLAS::FFLAS_SIDE side, const FFLAS::FFLAS_UPLO Uplo, const FFLAS::FFLAS_DIAG diagA, const FFLAS::FFLAS_DIAG diagB, const size_t N, typename Field::ConstElement_ptr A, const size_t lda, typename Field::Element_ptr B, const size_t ldb, const size_t threshold=64)
	Solve a triangular system with a triangular right hand side of the same shape. More...

template<class Field >
void	ftrssyr2k (const Field &F, const FFLAS::FFLAS_UPLO Uplo, const FFLAS::FFLAS_DIAG diagA, const size_t N, typename Field::ConstElement_ptr A, const size_t lda, typename Field::Element_ptr B, const size_t ldb, const size_t threshold=64)
	Solve a triangular system in a symmetric sum: find B upper/lower triangular such that A^T B + B^T A = C where C is symmetric. More...

template<class Field >
bool	fsytrf (const Field &F, const FFLAS::FFLAS_UPLO UpLo, const size_t N, typename Field::Element_ptr A, const size_t lda, const size_t threshold=__FFLASFFPACK_FSYTRF_THRESHOLD)
	Triangular factorization of symmetric matrices. More...

template<class Field >
bool	fsytrf_nonunit (const Field &F, const FFLAS::FFLAS_UPLO UpLo, const size_t N, typename Field::Element_ptr A, const size_t lda, typename Field::Element_ptr D, const size_t incD, const size_t threshold=__FFLASFFPACK_FSYTRF_THRESHOLD)
	Triangular factorization of symmetric matrices. More...

template<class Field >
size_t	PLUQ (const Field &F, const FFLAS::FFLAS_DIAG Diag, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t P, size_t Q)
	Compute a PLUQ factorization of the given matrix. More...

template<class Field >
size_t	LUdivine (const Field &F, const FFLAS::FFLAS_DIAG Diag, const FFLAS::FFLAS_TRANSPOSE trans, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t P, size_t Qt, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive, const size_t cutoff=__FFLASFFPACK_LUDIVINE_THRESHOLD)
	Compute the CUP or PLE factorization of the given matrix. More...

template<class Field >
size_t	ColumnEchelonForm (const Field &F, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t P, size_t Qt, bool transform=false, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive)
	Compute the Column Echelon form of the input matrix in-place. More...

template<class Field >
size_t	RowEchelonForm (const Field &F, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t P, size_t Qt, const bool transform=false, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive)
	Compute the Row Echelon form of the input matrix in-place. More...

template<class Field >
size_t	ReducedColumnEchelonForm (const Field &F, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t P, size_t Qt, const bool transform=false, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive)
	Compute the Reduced Column Echelon form of the input matrix in-place. More...

template<class Field >
size_t	ReducedRowEchelonForm (const Field &F, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t P, size_t Qt, const bool transform=false, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive)
	Compute the Reduced Row Echelon form of the input matrix in-place. More...

template<class Field >
Field::Element_ptr	Invert (const Field &F, const size_t M, typename Field::Element_ptr A, const size_t lda, int &nullity)
	Invert the given matrix in place or computes its nullity if it is singular. More...

template<class Field >
Field::Element_ptr	Invert (const Field &F, const size_t M, typename Field::ConstElement_ptr A, const size_t lda, typename Field::Element_ptr X, const size_t ldx, int &nullity)
	Invert the given matrix or computes its nullity if it is singular. More...

template<class Field >
Field::Element_ptr	Invert2 (const Field &F, const size_t M, typename Field::Element_ptr A, const size_t lda, typename Field::Element_ptr X, const size_t ldx, int &nullity)
	Invert the given matrix or computes its nullity if it is singular. More...

template<class PolRing >
std::list< typename PolRing::Element > &	CharPoly (const PolRing &R, std::list< typename PolRing::Element > &charp, const size_t N, typename PolRing::Domain_t::Element_ptr A, const size_t lda, typename PolRing::Domain_t::RandIter &G, const FFPACK_CHARPOLY_TAG CharpTag=FfpackAuto, const size_t degree=__FFLASFFPACK_ARITHPROG_THRESHOLD)
	Compute the characteristic polynomial of the matrix A. More...

template<class PolRing >
PolRing::Element &	CharPoly (const PolRing &R, typename PolRing::Element &charp, const size_t N, typename PolRing::Domain_t::Element_ptr A, const size_t lda, typename PolRing::Domain_t::RandIter &G, const FFPACK_CHARPOLY_TAG CharpTag=FfpackAuto, const size_t degree=__FFLASFFPACK_ARITHPROG_THRESHOLD)
	Compute the characteristic polynomial of the matrix A. More...

template<class PolRing >
PolRing::Element &	CharPoly (const PolRing &R, typename PolRing::Element &charp, const size_t N, typename PolRing::Domain_t::Element_ptr A, const size_t lda, const FFPACK_CHARPOLY_TAG CharpTag=FfpackAuto, const size_t degree=__FFLASFFPACK_ARITHPROG_THRESHOLD)
	Compute the characteristic polynomial of the matrix A. More...

template<class Field , class Polynomial >
Polynomial &	MinPoly (const Field &F, Polynomial &minP, const size_t N, typename Field::ConstElement_ptr A, const size_t lda)
	Compute the minimal polynomial of the matrix A. More...

template<class Field , class Polynomial , class RandIter >
Polynomial &	MinPoly (const Field &F, Polynomial &minP, const size_t N, typename Field::ConstElement_ptr A, const size_t lda, RandIter &G)
	Compute the minimal polynomial of the matrix A. More...

template<class Field , class Polynomial >
Polynomial &	MatVecMinPoly (const Field &F, Polynomial &minP, const size_t N, typename Field::ConstElement_ptr A, const size_t lda, typename Field::ConstElement_ptr v, const size_t incv)
	Compute the minimal polynomial of the matrix A and a vector v, namely the first linear dependency relation in the Krylov basis . More...

template<class Field >
size_t	Rank (const Field &F, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda)
	Computes the rank of the given matrix using a PLUQ factorization. More...

template<class Field >
bool	IsSingular (const Field &F, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda)
	Returns true if the given matrix is singular. More...

template<class Field >
Field::Element &	Det (const Field &F, typename Field::Element &det, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t P=NULL, size_t Q=NULL)
	Returns the determinant of the given square matrix. More...

template<class Field >
Field::Element_ptr	Solve (const Field &F, const size_t M, typename Field::Element_ptr A, const size_t lda, typename Field::Element_ptr x, const int incx, typename Field::ConstElement_ptr b, const int incb)
	Solves a linear system AX = b using PLUQ factorization. More...

template<class Field >
*void	RandomNullSpaceVector (const Field &F, const FFLAS::FFLAS_SIDE Side, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, typename Field::Element_ptr X, const size_t incX)
	Solve L X = B or X L = B in place. More...

template<class Field >
size_t	NullSpaceBasis (const Field &F, const FFLAS::FFLAS_SIDE Side, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, typename Field::Element_ptr &NS, size_t &ldn, size_t &NSdim)
	Computes a basis of the Left/Right nullspace of the matrix A. More...

template<class Field >
size_t	RowRankProfile (const Field &F, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t *&rkprofile, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive)
	Computes the row rank profile of A. More...

template<class Field >
size_t	ColumnRankProfile (const Field &F, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t *&rkprofile, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive)
	Computes the column rank profile of A. More...

void	RankProfileFromLU (const size_t P, const size_t N, const size_t R, size_t rkprofile, const FFPACK_LU_TAG LuTag)
	Recovers the column/row rank profile from the permutation of an LU decomposition. More...

size_t	LeadingSubmatrixRankProfiles (const size_t M, const size_t N, const size_t R, const size_t LSm, const size_t LSn, const size_t P, const size_t Q, size_t RRP, size_t CRP)
	Recovers the row and column rank profiles of any leading submatrix from the PLUQ decomposition. More...

template<class Field >
size_t	RowRankProfileSubmatrixIndices (const Field &F, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t &rowindices, size_t &colindices, size_t &R)
	RowRankProfileSubmatrixIndices. More...

template<class Field >
size_t	ColRankProfileSubmatrixIndices (const Field &F, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t &rowindices, size_t &colindices, size_t &R)
	Computes the indices of the submatrix r*r X of A whose columns correspond to the column rank profile of A. More...

template<class Field >
size_t	RowRankProfileSubmatrix (const Field &F, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, typename Field::Element_ptr &X, size_t &R)
	Computes the r*r submatrix X of A, by picking the row rank profile rows of A. More...

template<class Field >
size_t	ColRankProfileSubmatrix (const Field &F, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, typename Field::Element_ptr &X, size_t &R)
	Compute the $r\times r$ submatrix X of A, by picking the row rank profile rows of A. More...

template<class Field >
void	getTriangular (const Field &F, const FFLAS::FFLAS_UPLO Uplo, const FFLAS::FFLAS_DIAG diag, const size_t M, const size_t N, const size_t R, typename Field::ConstElement_ptr A, const size_t lda, typename Field::Element_ptr T, const size_t ldt, const bool OnlyNonZeroVectors=false)
	Extracts a triangular matrix from a compact storage A=L\U of rank R. More...

template<class Field >
void	getTriangular (const Field &F, const FFLAS::FFLAS_UPLO Uplo, const FFLAS::FFLAS_DIAG diag, const size_t M, const size_t N, const size_t R, typename Field::Element_ptr A, const size_t lda)
	Cleans up a compact storage A=L\U to reveal a triangular matrix of rank R. More...

template<class Field >
void	getEchelonForm (const Field &F, const FFLAS::FFLAS_UPLO Uplo, const FFLAS::FFLAS_DIAG diag, const size_t M, const size_t N, const size_t R, const size_t *P, typename Field::ConstElement_ptr A, const size_t lda, typename Field::Element_ptr T, const size_t ldt, const bool OnlyNonZeroVectors=false, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive)
	Extracts a matrix in echelon form from a compact storage A=L\U of rank R obtained by RowEchelonForm or ColumnEchelonForm. More...

template<class Field >
void	getEchelonForm (const Field &F, const FFLAS::FFLAS_UPLO Uplo, const FFLAS::FFLAS_DIAG diag, const size_t M, const size_t N, const size_t R, const size_t *P, typename Field::Element_ptr A, const size_t lda, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive)
	Cleans up a compact storage A=L\U obtained by RowEchelonForm or ColumnEchelonForm to reveal an echelon form of rank R. More...

template<class Field >
void	getEchelonTransform (const Field &F, const FFLAS::FFLAS_UPLO Uplo, const FFLAS::FFLAS_DIAG diag, const size_t M, const size_t N, const size_t R, const size_t P, const size_t Q, typename Field::ConstElement_ptr A, const size_t lda, typename Field::Element_ptr T, const size_t ldt, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive)
	Extracts a transformation matrix to echelon form from a compact storage A=L\U of rank R obtained by RowEchelonForm or ColumnEchelonForm. More...

template<class Field >
void	getReducedEchelonForm (const Field &F, const FFLAS::FFLAS_UPLO Uplo, const size_t M, const size_t N, const size_t R, const size_t *P, typename Field::ConstElement_ptr A, const size_t lda, typename Field::Element_ptr T, const size_t ldt, const bool OnlyNonZeroVectors=false, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive)
	Extracts a matrix in echelon form from a compact storage A=L\U of rank R obtained by ReducedRowEchelonForm or ReducedColumnEchelonForm with transform = true. More...

template<class Field >
void	getReducedEchelonForm (const Field &F, const FFLAS::FFLAS_UPLO Uplo, const size_t M, const size_t N, const size_t R, const size_t *P, typename Field::Element_ptr A, const size_t lda, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive)
	Cleans up a compact storage A=L\U of rank R obtained by ReducedRowEchelonForm or ReducedColumnEchelonForm with transform = true. More...

template<class Field >
void	getReducedEchelonTransform (const Field &F, const FFLAS::FFLAS_UPLO Uplo, const size_t M, const size_t N, const size_t R, const size_t P, const size_t Q, typename Field::ConstElement_ptr A, const size_t lda, typename Field::Element_ptr T, const size_t ldt, const FFPACK_LU_TAG LuTag=FfpackSlabRecursive)
	Extracts a transformation matrix to echelon form from a compact storage A=L\U of rank R obtained by RowEchelonForm or ColumnEchelonForm. More...

void	PLUQtoEchelonPermutation (const size_t N, const size_t R, const size_t P, size_t outPerm)
	Auxiliary routine: determines the permutation that changes a PLUQ decomposition into a echelon form revealing PLUQ decomposition.

template<class Field >
size_t	LTBruhatGen (const Field &Fi, const FFLAS::FFLAS_DIAG diag, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t P, size_t Q)
	LTBruhatGen Suppose A is Left Triangular Matrix This procedure computes the Bruhat Representation of A and return the rank of A. More...

template<class Field >
void	getLTBruhatGen (const Field &Fi, const size_t N, const size_t r, const size_t P, const size_t Q, typename Field::Element_ptr R, const size_t ldr)
	GetLTBruhatGen This procedure Computes the Rank Revealing Matrix based on the Bruhta representation of a Matrix. More...

template<class Field >
void	getLTBruhatGen (const Field &Fi, const FFLAS::FFLAS_UPLO Uplo, const FFLAS::FFLAS_DIAG diag, const size_t N, const size_t r, const size_t P, const size_t Q, typename Field::ConstElement_ptr A, const size_t lda, typename Field::Element_ptr T, const size_t ldt)
	GetLTBruhatGen This procedure computes the matrix L or U f the Bruhat Representation Suppose that A is the bruhat representation of a matrix. More...

size_t	LTQSorder (const size_t N, const size_t r, const size_t P, const size_t Q)
	LTQSorder This procedure computes the order of quasiseparability of a matrix. More...

template<class Field >
size_t	CompressToBlockBiDiagonal (const Field &Fi, const FFLAS::FFLAS_UPLO Uplo, size_t N, size_t s, size_t r, const size_t P, const size_t Q, typename Field::Element_ptr A, size_t lda, typename Field::Element_ptr X, size_t ldx, size_t K, size_t M, size_t *T)
	CompressToBlockBiDiagonal This procedure compress a compact representation of a row echelon form or column echelon form. More...

template<class Field >
void	ExpandBlockBiDiagonalToBruhat (const Field &Fi, const FFLAS::FFLAS_UPLO Uplo, size_t N, size_t s, size_t r, typename Field::Element_ptr A, size_t lda, typename Field::Element_ptr X, size_t ldx, size_t NbBlocks, size_t K, size_t M, size_t *T)
	ExpandBlockBiDiagonal This procedure expand a compact representation of a row echelon form or column echelon form. More...

void	Bruhat2EchelonPermutation (size_t N, size_t R, const size_t P, const size_t Q, size_t *M)
	Bruhat2EchelonPermutation (N,R,P,Q) Compute M such that LM or MU is in echelon form where L or U are factors of the Bruhat Rpresentation. More...

template<class Field >
void	productBruhatxTS (const Field &Fi, size_t N, size_t s, size_t r, const size_t P, const size_t Q, const typename Field::Element_ptr Xu, size_t ldu, size_t NbBlocksU, size_t Ku, size_t Tu, size_t MU, const typename Field::Element_ptr Xl, size_t ldl, size_t NbBlocksL, size_t Kl, size_t Tl, size_t ML, typename Field::Element_ptr B, size_t t, size_t ldb, typename Field::Element_ptr C, size_t ldc)
	productBruhatxTS Comput the product between the CRE compact representation of a matrix A and B a tall matrix

template<class Field >
Field::Element_ptr	LQUPtoInverseOfFullRankMinor (const Field &F, const size_t rank, typename Field::Element_ptr A_factors, const size_t lda, const size_t *QtPointer, typename Field::Element_ptr X, const size_t ldx)
	LQUPtoInverseOfFullRankMinor. More...

template<class Field >
void	RandomNullSpaceVector (const Field &F, const FFLAS::FFLAS_SIDE Side, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, typename Field::Element_ptr X, const size_t incX)
	Solve L X = B or X L = B in place. More...

template<class Field >
Field::Element_ptr	expandLCRE (const Field &Fi, size_t N, size_t s, size_t r, size_t R, size_t i, typename Field::ConstElement_ptr Xu, size_t ldu, size_t NbBlocksU, const size_t Ku, const size_t Tuinv, typename Field::ConstElement_ptr Xl, size_t ldl, size_t NbBlocksL, const size_t Kl, const size_t *Tlinv, typename Field::Element_ptr CRE, size_t ldcre)
	Expands an anti-diagonal block of a left triangular matrix from its compact Bruhat representation.

template<class Field >
void	productBruhatxTS (const Field &Fi, size_t N, size_t s, size_t r, size_t t, const size_t P, const size_t Q, typename Field::ConstElement_ptr Xu, size_t ldu, size_t NbBlocksU, const size_t Ku, const size_t Tu, const size_t MU, typename Field::ConstElement_ptr Xl, size_t ldl, size_t NbBlocksL, const size_t Kl, const size_t Tl, const size_t ML, typename Field::Element_ptr B, size_t ldb, const typename Field::Element beta, typename Field::Element_ptr D, size_t ldd)
	Compute the product of a left-triangular quasi-separable matrix A, represented by a compact Bruhat generator, with a dense rectangular matrix B: $C \gets A \times B + beta C$ . More...

template<class Field >
Field::Element_ptr	buildMatrix (const Field &F, typename Field::ConstElement_ptr E, typename Field::ConstElement_ptr C, const size_t lda, const size_t B, const size_t T, const size_t me, const size_t mc, const size_t lambda, const size_t mu)

template<class Field >
size_t	fsytrf_UP_RPM (const Field &Fi, const size_t N, typename Field::Element_ptr A, const size_t lda, typename Field::Element_ptr Dinv, const size_t incDinv, size_t *P, size_t BCThreshold)

template<class Field >
size_t	LUdivine (const Field &F, const FFLAS::FFLAS_DIAG Diag, const FFLAS::FFLAS_TRANSPOSE trans, const size_t M, const size_t N, typename Field::Element_ptr A, const size_t lda, size_t P, size_t Q, const FFPACK::FFPACK_LU_TAG LuTag, const size_t cutoff)

void	composePermutationsLLL (size_t P1, const size_t P2, const size_t R, const size_t N)
	Computes P1 x Diag (I_R, P2) where P1 is a LAPACK and P2 a LAPACK permutation and store the result in P1 as a LAPACK permutation. More...

void	composePermutationsLLM (size_t MathP, const size_t P1, const size_t *P2, const size_t R, const size_t N)
	Computes P1 x Diag (I_R, P2) where P1 is a LAPACK and P2 a LAPACK permutation and store the result in MathP as a MathPermutation format. More...

void	composePermutationsMLM (size_t MathP1, const size_t P2, const size_t R, const size_t N)
	Computes MathP1 x Diag (I_R, P2) where MathP1 is a MathPermutation and P2 a LAPACK permutation and store the result in MathP1 as a MathPermutation format. More...

template<class Field , class RandIter >
Field::Element_ptr	NonZeroRandomMatrix (const Field &F, size_t m, size_t n, typename Field::Element_ptr A, size_t lda, RandIter &G)
	Random non-zero Matrix. More...

template<class Field , class RandIter >
Field::Element_ptr	NonZeroRandomMatrix (const Field &F, size_t m, size_t n, typename Field::Element_ptr A, size_t lda)
	Random non-zero Matrix. More...

template<class Field , class RandIter >
Field::Element_ptr	RandomMatrix (const Field &F, size_t m, size_t n, typename Field::Element_ptr A, size_t lda, RandIter &G)
	Random Matrix. More...

template<class Field >
Field::Element_ptr	RandomMatrix (const Field &F, size_t m, size_t n, typename Field::Element_ptr A, size_t lda)
	Random Matrix. More...

template<class Field , class RandIter >
Field::Element_ptr	RandomTriangularMatrix (const Field &F, size_t m, size_t n, const FFLAS::FFLAS_UPLO UpLo, const FFLAS::FFLAS_DIAG Diag, bool nonsingular, typename Field::Element_ptr A, size_t lda, RandIter &G)
	Random Triangular Matrix. More...

template<class Field >
Field::Element_ptr	RandomTriangularMatrix (const Field &F, size_t m, size_t n, const FFLAS::FFLAS_UPLO UpLo, const FFLAS::FFLAS_DIAG Diag, bool nonsingular, typename Field::Element_ptr A, size_t lda)
	Random Triangular Matrix. More...

template<class Field , class RandIter >
Field::Element_ptr	RandomSymmetricMatrix (const Field &F, size_t n, bool nonsingular, typename Field::Element_ptr A, size_t lda, RandIter &G)
	Random Symmetric Matrix. More...

template<class Field , class RandIter >
Field::Element_ptr	RandomMatrixWithRank (const Field &F, size_t m, size_t n, size_t r, typename Field::Element_ptr A, size_t lda, RandIter &G)
	Random Matrix with prescribed rank. More...

template<class Field >
Field::Element_ptr	RandomMatrixWithRank (const Field &F, size_t m, size_t n, size_t r, typename Field::Element_ptr A, size_t lda)
	Random Matrix with prescribed rank. More...

size_t *	RandomIndexSubset (size_t N, size_t R, size_t *P)
	Pick uniformly at random a sequence of `R` distinct elements from the set $\{0,\dots, N-1\}$ using Knuth's shuffle. More...

size_t *	RandomPermutation (size_t N, size_t *P)
	Pick uniformly at random a permutation of size `N` stored in LAPACK format using Knuth's shuffle. More...

void	RandomRankProfileMatrix (size_t M, size_t N, size_t R, size_t rows, size_t cols)
	Pick uniformly at random an R-subpermutation of dimension `M` x `N` : a matrix with only R non-zeros equal to one, in a random rook placement. More...

void	RandomSymmetricRankProfileMatrix (size_t N, size_t R, size_t rows, size_t cols)
	Pick uniformly at random a symmetric R-subpermutation of dimension `N` x `N` : a symmetric matrix with only R non-zeros, all equal to one, in a random rook placement. More...

template<class Field , class RandIter >
Field::Element_ptr	RandomMatrixWithRankandRPM (const Field &F, size_t M, size_t N, size_t R, typename Field::Element_ptr A, size_t lda, const size_t RRP, const size_t CRP, RandIter &G)
	Random Matrix with prescribed rank and rank profile matrix Creates an `m` x `n` matrix with random entries and rank `r`. More...

template<class Field >
Field::Element_ptr	RandomMatrixWithRankandRPM (const Field &F, size_t M, size_t N, size_t R, typename Field::Element_ptr A, size_t lda, const size_t RRP, const size_t CRP)
	Random Matrix with prescribed rank and rank profile matrix Creates an `m` x `n` matrix with random entries and rank `r`. More...

template<class Field , class RandIter >
Field::Element_ptr	RandomSymmetricMatrixWithRankandRPM (const Field &F, size_t N, size_t R, typename Field::Element_ptr A, size_t lda, const size_t RRP, const size_t CRP, RandIter &G)
	Random Symmetric Matrix with prescribed rank and rank profile matrix Creates an `n` x `n` symmetric matrix with random entries and rank `r`. More...

template<class Field >
Field::Element_ptr	RandomSymmetricMatrixWithRankandRPM (const Field &F, size_t M, size_t N, size_t R, typename Field::Element_ptr A, size_t lda, const size_t RRP, const size_t CRP)
	Random Symmetric Matrix with prescribed rank and rank profile matrix Creates an `n` x `n` symmetric matrix with random entries and rank `r`. More...

template<class Field , class RandIter >
Field::Element_ptr	RandomMatrixWithRankandRandomRPM (const Field &F, size_t M, size_t N, size_t R, typename Field::Element_ptr A, size_t lda, RandIter &G)
	Random Matrix with prescribed rank, with random rank profile matrix Creates an `m` x `n` matrix with random entries, rank `r` and with a rank profile matrix chosen uniformly at random. More...

template<class Field >
Field::Element_ptr	RandomMatrixWithRankandRandomRPM (const Field &F, size_t M, size_t N, size_t R, typename Field::Element_ptr A, size_t lda)
	Random Matrix with prescribed rank, with random rank profile matrix Creates an `m` x `n` matrix with random entries, rank `r` and with a rank profile matrix chosen uniformly at random. More...

template<class Field , class RandIter >
Field::Element_ptr	RandomSymmetricMatrixWithRankandRandomRPM (const Field &F, size_t N, size_t R, typename Field::Element_ptr A, size_t lda, RandIter &G)
	Random Symmetric Matrix with prescribed rank, with random rank profile matrix Creates an `n` x `n` matrix with random entries, rank `r` and with a rank profile matrix chosen uniformly at random. More...

template<class Field >
Field::Element_ptr	RandomSymmetricMatrixWithRankandRandomRPM (const Field &F, size_t N, size_t R, typename Field::Element_ptr A, size_t lda)
	Random Symmetric Matrix with prescribed rank, with random rank profile matrix Creates an `n` x `n` matrix with random entries, rank `r` and with a rank profile matrix chosen uniformly at random. More...

template<class Field >
Field::Element_ptr	RandomMatrixWithDet (const Field &F, size_t n, const typename Field::Element d, typename Field::Element_ptr A, size_t lda)
	Random Matrix with prescribed det. More...

template<class Field , class RandIter >
Field::Element_ptr	RandomMatrixWithDet (const Field &F, size_t n, const typename Field::Element d, typename Field::Element_ptr A, size_t lda, RandIter &G)
	Random Matrix with prescribed det. More...

Detailed Description

Finite Field PACK Set of elimination based routines for dense linear algebra.

This namespace enlarges the set of BLAS routines of the class FFLAS, with higher level routines based on elimination.

Function Documentation

◆ applyP()

void applyP	(	const Field &	F,
		const FFLAS::FFLAS_SIDE	Side,
		const FFLAS::FFLAS_TRANSPOSE	Trans,
		const size_t	M,
		const size_t	ibeg,
		const size_t	iend,
		typename Field::Element_ptr	A,
		const size_t	lda,
		const size_t *	P
	)

inline

Computes P1 x Diag (I_R, P2) where P1 is a LAPACK and P2 a LAPACK permutation and store the result in P1 as a LAPACK permutation.

Parameters

[in,out]	P1	a LAPACK permutation of size N
	P2	a LAPACK permutation of size N-R

Applies a permutation P to the matrix A. Apply a permutation P, stored in the LAPACK format (a sequence of transpositions) between indices ibeg and iend of P to (iend-ibeg) vectors of size M stored in A (as column for NoTrans and rows for Trans). Side==FFLAS::FflasLeft for row permutation Side==FFLAS::FflasRight for a column permutation Trans==FFLAS::FflasTrans for the inverse permutation of P

Parameters

F	base field
Side	decides if rows (FflasLeft) or columns (FflasRight) are permuted
Trans	decides if the matrix is seen as columns (FflasTrans) or rows (FflasNoTrans)
M	size of the elements to permute
ibeg	first index to consider in P
iend	last index to consider in P
A	input matrix
lda	leading dimension of A
P	permutation in LAPACK format
psh	(optional): a sequential or parallel helper, to choose between sequential or parallel execution

Warning: not sure the submatrix is still a permutation and the one we expect in all cases... examples for iend=2, ibeg=1 and P=[2,2,2]

◆ MonotonicApplyP()

void MonotonicApplyP	(	const Field &	F,
		const FFLAS::FFLAS_SIDE	Side,
		const FFLAS::FFLAS_TRANSPOSE	Trans,
		const size_t	M,
		const size_t	ibeg,
		const size_t	iend,
		typename Field::Element_ptr	A,
		const size_t	lda,
		const size_t *	P,
		const size_t	R
	)

inline

Apply a R-monotonically increasing permutation P, to the matrix A.

MonotonicApplyP Apply a permutation defined by the first R entries of the vector P (the pivots).

The permutation represented by P is defined as follows:

the first R values of P is a LAPACK reprensentation (a sequence of transpositions)

the remaining iend-ibeg-R values of the permutation are in a monotonically increasing progression Side==FFLAS::FflasLeft for row permutation Side==FFLAS::FflasRight for a column permutation Trans==FFLAS::FflasTrans for the inverse permutation of P

Parameters

F	base field
Side	selects if it is a row (FflasLeft) or column (FflasRight) permutation
Trans	inverse permutation (FflasTrans/NoTrans)
M
ibeg
iend
A	input matrix
lda	leading dimension of A
P	LAPACK permuation
R	first values of P

The non pivot elements, are located in montonically increasing order.

◆ fgetrs() [1/2]

void fgetrs	(	const Field &	F,
		const FFLAS::FFLAS_SIDE	Side,
		const size_t	M,
		const size_t	N,
		const size_t	R,
		typename Field::Element_ptr	A,
		const size_t	lda,
		const size_t *	P,
		const size_t *	Q,
		typename Field::Element_ptr	B,
		const size_t	ldb,
		int *	info
	)

Solve the system or .

Solving using the PLUQ decomposition of A already computed inplace with PLUQ (FFLAS::FflasNonUnit). Version for A square. If A is rank deficient, a solution is returned if the system is consistent, Otherwise an info is 1

Parameters

F	base field
Side	Determine wheter the resolution is left (FflasLeft) or right (FflasRight) looking.
M	row dimension of `B`
N	col dimension of `B`
R	rank of `A`
A	input matrix
lda	leading dimension of `A`
P	row permutation of the `PLUQ` decomposition of `A`
Q	column permutation of the `PLUQ` decomposition of `A`
B	Right/Left hand side matrix. Initially stores `B`, finally stores the solution `X`.
ldb	leading dimension of `B`
info	Success of the computation: 0 if successfull, >0 if system is inconsistent

◆ fgetrs() [2/2]

Field::Element_ptr fgetrs	(	const Field &	F,
		const FFLAS::FFLAS_SIDE	Side,
		const size_t	M,
		const size_t	N,
		const size_t	NRHS,
		const size_t	R,
		typename Field::Element_ptr	A,
		const size_t	lda,
		const size_t *	P,
		const size_t *	Q,
		typename Field::Element_ptr	X,
		const size_t	ldx,
		typename Field::ConstElement_ptr	B,
		const size_t	ldb,
		int *	info
	)

Solve the system A X = B or X A = B.

Solving using the PLUQ decomposition of A already computed inplace with PLUQ(FFLAS::FflasNonUnit). Version for A rectangular. If A is rank deficient, a solution is returned if the system is consistent, Otherwise an info is 1

Parameters

F	base field
Side	Determine wheter the resolution is left (FflasLeft) or right (FflasRight) looking.
M	row dimension of A
N	col dimension of A
NRHS	number of columns (if Side = FFLAS::FflasLeft) or row (if Side = FFLAS::FflasRight) of the matrices X and B
R	rank of A
A	input matrix
lda	leading dimension of A
P	row permutation of the PLUQ decomposition of A
Q	column permutation of the PLUQ decomposition of A
X	solution matrix
ldx	leading dimension of X
B	Right/Left hand side matrix.
ldb	leading dimension of B
info	Succes of the computation: 0 if successfull, >0 if system is inconsistent

◆ fgesv() [1/2]

size_t fgesv	(	const Field &	F,
		const FFLAS::FFLAS_SIDE	Side,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	B,
		const size_t	ldb,
		int *	info
	)

Square system solver.

Parameters

F	The computation domain
Side	Determine wheter the resolution is left (FflasLeft) or right (FflasRight) looking
M	row dimension of B
N	col dimension of B
A	input matrix
lda	leading dimension of A
B	Right/Left hand side matrix. Initially contains B, finally contains the solution X.
ldb	leading dimension of B
info	Success of the computation: 0 if successfull, >0 if system is inconsistent

Returns: the rank of the system

Solve the system A X = B or X A = B. Version for A square. If A is rank deficient, a solution is returned if the system is consistent, Otherwise an info is 1

◆ fgesv() [2/2]

size_t fgesv	(	const Field &	F,
		const FFLAS::FFLAS_SIDE	Side,
		const size_t	M,
		const size_t	N,
		const size_t	NRHS,
		typename Field::Element_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	X,
		const size_t	ldx,
		typename Field::ConstElement_ptr	B,
		const size_t	ldb,
		int *	info
	)

Rectangular system solver.

Parameters

F	The computation domain
Side	Determine wheter the resolution is left (FflasLeft) or right (FflasRight) looking
M	row dimension of A
N	col dimension of A
NRHS	number of columns (if Side = FFLAS::FflasLeft) or row (if Side = FFLAS::FflasRight) of the matrices X and B
A	input matrix
lda	leading dimension of A
B	Right/Left hand side matrix. Initially contains B, finally contains the solution X.
ldb	leading dimension of B
X
ldx
info	Success of the computation: 0 if successfull, >0 if system is inconsistent

Returns: the rank of the system

Solve the system A X = B or X A = B. Version for A square. If A is rank deficient, a solution is returned if the system is consistent, Otherwise an info is 1

◆ ftrtri()

void ftrtri	(	const Field &	F,
		const FFLAS::FFLAS_UPLO	Uplo,
		const FFLAS::FFLAS_DIAG	Diag,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		const size_t	threshold = `__FFLASFFPACK_FTRTRI_THRESHOLD`
	)

Compute the inverse of a triangular matrix.

Parameters

F	base field
Uplo	whether the matrix is upper or lower triangular
Diag	whether the matrix is unit diagonal (FflasUnit/NoUnit)
N	input matrix order
A	the input matrix
lda	leading dimension of A

◆ ftrtrm()

void ftrtrm	(	const Field &	F,
		const FFLAS::FFLAS_SIDE	side,
		const FFLAS::FFLAS_DIAG	diag,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda
	)

Compute the product of two triangular matrices of opposite shape.

Product UL or LU of the upper, resp lower triangular matrices U and L stored one above the other in the square matrix A.

Parameters

F	base field
Side	set to FflasLeft to compute the product UL, FflasRight to compute LU
diag	whether the matrix U is unit diagonal (FflasUnit/NoUnit)
N	input matrix order
A	the input matrix
lda	leading dimension of A

◆ ftrstr()

void ftrstr	(	const Field &	F,
		const FFLAS::FFLAS_SIDE	side,
		const FFLAS::FFLAS_UPLO	Uplo,
		const FFLAS::FFLAS_DIAG	diagA,
		const FFLAS::FFLAS_DIAG	diagB,
		const size_t	N,
		typename Field::ConstElement_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	B,
		const size_t	ldb,
		const size_t	threshold = `64`
	)

inline

Solve a triangular system with a triangular right hand side of the same shape.

Parameters

F	base field
Side	set to FflasLeft to compute U1^-1U2 or L1^-1L2, FflasRight to compute U1U2^-1 or L1L2^-1
Uplo	whether the matrix A is upper or lower triangular
diag1	whether the matrix U1 or L2 is unit diagonal (FflasUnit/NoUnit)
diag2	whether the matrix U2 or L2 is unit diagonal (FflasUnit/NoUnit)
N	order of the input matrices
A	the input matrix to be inverted (U1 or L1)
lda	leading dimension of A
B	the input right hand side (U2 or L2)
ldb	leading dimension of B

◆ ftrssyr2k()

void ftrssyr2k	(	const Field &	F,
		const FFLAS::FFLAS_UPLO	Uplo,
		const FFLAS::FFLAS_DIAG	diagA,
		const size_t	N,
		typename Field::ConstElement_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	B,
		const size_t	ldb,
		const size_t	threshold = `64`
	)

inline

Solve a triangular system in a symmetric sum: find B upper/lower triangular such that A^T B + B^T A = C where C is symmetric.

C is overwritten by B.

Parameters

	F	base field
	Side	set to FflasLeft to compute U1^-1U2 or L1^-1L2, FflasRight to compute U1U2^-1 or L1L2^-1
	Uplo	whether the matrix A is upper or lower triangular
	diagA	whether the matrix A is unit diagonal (FflasUnit/NoUnit)
	N	order of the input matrices
	A	the input matrix
	lda	leading dimension of A
[in,out]	B	the input right hand side where the output is written
	ldb	leading dimension of B

◆ fsytrf()

bool fsytrf	(	const Field &	F,
		const FFLAS::FFLAS_UPLO	UpLo,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		const size_t	threshold = `__FFLASFFPACK_FSYTRF_THRESHOLD`
	)

Triangular factorization of symmetric matrices.

Parameters

	F	The computation domain
	UpLo	Determine wheter to store the upper (FflasUpper) or lower (FflasLower) triangular factor
	N	order of the matrix A
[in,out]	A	input matrix
	lda	leading dimension of A

Returns: false if the A does not have generic rank profile, making the computation fail.

Compute the a triangular factorization of the matrix A: $A = L \times D \times L^T$ if UpLo = FflasLower or $A = U^T \times D \times U$ otherwise. D is a diagonal matrix. The matrices L and U are unit diagonal lower (resp. upper) triangular and overwrite the input matrix A. The matrix D is stored on the diagonal of A, as the diagonal of L or U is known to be all ones. If A does not have generic rank profile, the LDLT or UTDU factorizations is not defined, and the algorithm returns false.

◆ fsytrf_nonunit()

bool fsytrf_nonunit	(	const Field &	F,
		const FFLAS::FFLAS_UPLO	UpLo,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	D,
		const size_t	incD,
		const size_t	threshold = `__FFLASFFPACK_FSYTRF_THRESHOLD`
	)

Triangular factorization of symmetric matrices.

Parameters

	F	The computation domain
	UpLo	Determine wheter to store the upper (FflasUpper) or lower (FflasLower) triangular factor
	N	order of the matrix A
[in,out]	A	input matrix
[in,out]	D
	lda	leading dimension of A

Returns: false if the A does not have generic rank profile, making the computation fail.

Compute the a triangular factorization of the matrix A: $A = L \times Dinv \times L^T$ if UpLo = FflasLower or $A = U^T \times D \times U$ otherwise. D is a diagonal matrix. The matrices L and U are lower (resp. upper) triangular and overwrite the input matrix A. The matrix D need to be stored separately, as the diagonal of L or U are not unit. If A does not have generic rank profile, the LDLT or UTDU factorizations is not defined, and the algorithm returns false.

◆ PLUQ()

size_t PLUQ	(	const Field &	F,
		const FFLAS::FFLAS_DIAG	Diag,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *	P,
		size_t *	Q
	)

inline

Compute a PLUQ factorization of the given matrix.

Return its rank. The permutations P and Q are represented using LAPACK's convention.

Parameters

F	base field
Diag	whether U should have a unit diagonal (FflasUnit) or not (FflasNoUnit)
M	matrix row dimension
N	matrix column dimension
A	input matrix
lda	leading dimension of `A`
P	the row permutation
Q	the column permutation

Returns: the rank of A

Bibliography:

Dumas J-G., Pernet C., and Sultan Z. Simultaneous computation of the row and column rank profiles , ISSAC'13, 2013

◆ LUdivine() [1/2]

size_t LUdivine	(	const Field &	F,
		const FFLAS::FFLAS_DIAG	Diag,
		const FFLAS::FFLAS_TRANSPOSE	trans,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *	P,
		size_t *	Qt,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`,
		const size_t	cutoff = `__FFLASFFPACK_LUDIVINE_THRESHOLD`
	)

Compute the CUP or PLE factorization of the given matrix.

Using a block algorithm and return its rank. The permutations P and Q are represented using LAPACK's convention.

Parameters

F	base field
Diag	whether the transformation matrix (U of the CUP, L of the PLE) should have a unit diagonal (FflasUnit) or not (FflasNoUnit)
trans	whether to compute the CUP decomposition (FflasNoTrans) or the PLE decomposition (FflasTrans)
M	matrix row dimension
N	matrix column dimension
A	input matrix
lda	leading dimension of `A`
P	the factor of CUP or PLE
Q	a permutation indicating the pivot position in the echelon form C or E in its first r positions
LuTag	flag for setting the earling termination if the matrix is singular
cutoff	threshold to basecase

Returns: the rank of A

Bibliography:

Jeannerod C-P, Pernet, C. and Storjohann, A. Rank-profile revealing Gaussian elimination and the CUP matrix decomposition , J. of Symbolic Comp., 2013
Pernet C, Brassel M LUdivine, une divine factorisation LU, 2002

◆ ColumnEchelonForm()

size_t ColumnEchelonForm	(	const Field &	F,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *	P,
		size_t *	Qt,
		bool	transform = `false`,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`
	)

inline

Compute the Column Echelon form of the input matrix in-place.

If LuTag == FfpackTileRecursive, then after the computation A = [ M \ V ] such that AU = C is a column echelon decomposition of A, with U = P^T [ V ] and C = M + Q [ Ir ] [ 0 In-r ] [ 0 ] If LuTag == FfpackTileRecursive then A = [ N \ V ] such that the same holds with M = Q N

Qt = Q^T If transform=false, the matrix V is not computed. See also test-colechelon for an example of use

Parameters

	F	base field
	M	number of rows
	N	number of columns
[in]	A	input matrix
	lda	leading dimension of A
	P	the column permutation
	Qt	the row position of the pivots in the echelon form
	transform	decides whether V is computed
	LuTag	chooses the elimination algorithm. SlabRecursive for LUdivine, TileRecursive for PLUQ

◆ RowEchelonForm()

size_t RowEchelonForm	(	const Field &	F,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *	P,
		size_t *	Qt,
		const bool	transform = `false`,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`
	)

inline

Compute the Row Echelon form of the input matrix in-place.

If LuTag == FfpackTileRecursive, then after the computation A = [ L \ M ] such that X A = R is a row echelon decomposition of A, with X = [ L 0 ] P and R = M + [Ir 0] Q^T [ In-r] If LuTag == FfpackTileRecursive then A = [ L \ N ] such that the same holds with M = N Q^T Qt = Q^T If transform=false, the matrix L is not computed. See also test-rowechelon for an example of use

Parameters

	F	base field
	M	number of rows
	N	number of columns
[in]	A	the input matrix
	lda	leading dimension of A
	P	the row permutation
	Qt	the column position of the pivots in the echelon form
	transform	decides whether L is computed
	LuTag	chooses the elimination algorithm. SlabRecursive for LUdivine, TileRecursive for PLUQ

◆ ReducedColumnEchelonForm()

size_t ReducedColumnEchelonForm	(	const Field &	F,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *	P,
		size_t *	Qt,
		const bool	transform = `false`,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`
	)

inline

Compute the Reduced Column Echelon form of the input matrix in-place.

After the computation A = [ V ] such that AX = R is a reduced col echelon [ M 0 ] decomposition of A, where X = P^T [ V ] and R = Q [ Ir ] [ 0 In-r ] [ M 0 ] Qt = Q^T If transform=false, the matrix X is not computed and the matrix A = R

Parameters

	F	base field
	M	number of rows
	N	number of columns
[in]	A	input matrix
	lda	leading dimension of A
	P	the column permutation
	Qt	the row position of the pivots in the echelon form
	transform	decides whether X is computed
	LuTag	chooses the elimination algorithm. SlabRecursive for LUdivine, TileRecursive for PLUQ

◆ ReducedRowEchelonForm()

size_t ReducedRowEchelonForm	(	const Field &	F,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *	P,
		size_t *	Qt,
		const bool	transform = `false`,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`
	)

inline

Compute the Reduced Row Echelon form of the input matrix in-place.

After the computation A = [ V1 M ] such that X A = R is a reduced row echelon [ V2 0 ] decomposition of A, where X = [ V1 0 ] P and R = [ Ir M ] Q^T [ V2 In-r ] [ 0 ] Qt = Q^T If transform=false, the matrix X is not computed and the matrix A = R

Parameters

	F	base field
	M	number of rows
	N	number of columns
[in]	A	input matrix
	lda	leading dimension of A
	P	the row permutation
	Qt	the column position of the pivots in the echelon form
	transform	decides whether X is computed
	LuTag	chooses the elimination algorithm. SlabRecursive for LUdivine, TileRecursive for PLUQ

◆ Invert() [1/2]

Field::Element_ptr Invert	(	const Field &	F,
		const size_t	M,
		typename Field::Element_ptr	A,
		const size_t	lda,
		int &	nullity
	)

Invert the given matrix in place or computes its nullity if it is singular.

An inplace algorithm is used.

Parameters

	F	The computation domain
	M	order of the matrix
[in,out]	A	input matrix ( $M \times M$ )
	lda	leading dimension of A
	nullity	dimension of the kernel of A

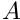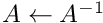
Returns: pointer to and $A \gets A^{-1}$

◆ Invert() [2/2]

Field::Element_ptr Invert	(	const Field &	F,
		const size_t	M,
		typename Field::ConstElement_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	X,
		const size_t	ldx,
		int &	nullity
	)

Invert the given matrix or computes its nullity if it is singular.

Precondition: X is preallocated and should be large enough to store the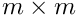 $m \times m$ matrix A.

Parameters

	F	The computation domain
	M	order of the matrix
[in]	A	input matrix ( $M \times M$ )
	lda	leading dimension of `A`
[out]	X	this is the inverse of `A` if `A` is invertible (non `NULL` and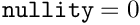 $\mathtt{nullity} = 0$ ). It is untouched otherwise.
	ldx	leading dimension of `X`
	nullity	dimension of the kernel of `A`

Returns: pointer to $X = A^{-1}$

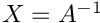
◆ Invert2()

Field::Element_ptr Invert2	(	const Field &	F,
		const size_t	M,
		typename Field::Element_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	X,
		const size_t	ldx,
		int &	nullity
	)

Invert the given matrix or computes its nullity if it is singular.

An algorithm is used. This routine can be % faster than FFPACK::Invert but is not totally inplace.

Precondition: X is preallocated and should be large enough to store the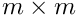 $m \times m$ matrix A.

Warning: A is overwritten here !

Bug:: not tested.

Parameters

	F	the computation domain
	M	order of the matrix
[in,out]	A	input matrix ( $M \times M$ ). On output, `A` is modified and represents a "psycological" factorisation `LU`.
	lda	leading dimension of A
[out]	X	this is the inverse of `A` if `A` is invertible (non `NULL` and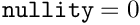 $\mathtt{nullity} = 0$ ). It is untouched otherwise.
	ldx	leading dimension of `X`
	nullity	dimension of the kernel of `A`

Returns: pointer to $X = A^{-1}$

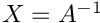
Todo:: this init is not all necessary (done after ftrtri)

Todo:: this init is not all necessary (done after ftrtri)

◆ CharPoly() [1/3]

std::list< typename PolRing::Element > & CharPoly	(	const PolRing &	R,
		std::list< typename PolRing::Element > &	charp,
		const size_t	N,
		typename PolRing::Domain_t::Element_ptr	A,
		const size_t	lda,
		typename PolRing::Domain_t::RandIter &	G,
		const FFPACK_CHARPOLY_TAG	CharpTag = `FfpackAuto`,
		const size_t	degree = `__FFLASFFPACK_ARITHPROG_THRESHOLD`
	)

inline

Compute the characteristic polynomial of the matrix A.

Parameters

	R	the polynomial ring of charp (contains the base field)
[out]	charp	the characteristic polynomial of `as` a list of factors
	N	order of the matrix `A`
[in]	A	the input matrix ( $N \times N$ ) (could be overwritten in some algorithmic variants)
	lda	leading dimension of `A`
	CharpTag	the algorithmic variant
	G	a random iterator (required for the randomized variants LUKrylov and ArithProg)

◆ CharPoly() [2/3]

PolRing::Element & CharPoly	(	const PolRing &	R,
		typename PolRing::Element &	charp,
		const size_t	N,
		typename PolRing::Domain_t::Element_ptr	A,
		const size_t	lda,
		typename PolRing::Domain_t::RandIter &	G,
		const FFPACK_CHARPOLY_TAG	CharpTag = `FfpackAuto`,
		const size_t	degree = `__FFLASFFPACK_ARITHPROG_THRESHOLD`
	)

inline

Compute the characteristic polynomial of the matrix A.

Parameters

	R	the polynomial ring of charp (contains the base field)
[out]	charp	the characteristic polynomial of `as` a single polynomial
	N	order of the matrix `A`
[in]	A	the input matrix ( $N \times N$ ) (could be overwritten in some algorithmic variants)
	lda	leading dimension of `A`
	CharpTag	the algorithmic variant
	G	a random iterator (required for the randomized variants LUKrylov and ArithProg)

◆ CharPoly() [3/3]

PolRing::Element & CharPoly	(	const PolRing &	R,
		typename PolRing::Element &	charp,
		const size_t	N,
		typename PolRing::Domain_t::Element_ptr	A,
		const size_t	lda,
		const FFPACK_CHARPOLY_TAG	CharpTag = `FfpackAuto`,
		const size_t	degree = `__FFLASFFPACK_ARITHPROG_THRESHOLD`
	)

inline

Compute the characteristic polynomial of the matrix A.

Parameters

	R	the polynomial ring of charp (contains the base field)
[out]	charp	the characteristic polynomial of `as` a single polynomial
	N	order of the matrix `A`
[in]	A	the input matrix ( $N \times N$ ) (could be overwritten in some algorithmic variants)
	lda	leading dimension of `A`
	CharpTag	the algorithmic variant

◆ MinPoly() [1/2]

Polynomial & MinPoly	(	const Field &	F,
		Polynomial &	minP,
		const size_t	N,
		typename Field::ConstElement_ptr	A,
		const size_t	lda
	)

inline

Compute the minimal polynomial of the matrix A.

The algorithm is randomized probabilistic, and computes the minimal polynomial of the Krylov iterates of a random vector: (v, Av, .., A^kv)

Parameters

	F	the base field
[out]	minP	the minimal polynomial of `A`
	N	order of the matrix `A`
[in]	A	the input matrix ( $N \times N$ )
	lda	leading dimension of `A`

◆ MinPoly() [2/2]

Polynomial & MinPoly	(	const Field &	F,
		Polynomial &	minP,
		const size_t	N,
		typename Field::ConstElement_ptr	A,
		const size_t	lda,
		RandIter &	G
	)

inline

Compute the minimal polynomial of the matrix A.

The algorithm is randomized probabilistic, and computes the minimal polynomial of the Krylov iterates of a random vector: (v, Av, .., A^kv)

Parameters

	F	the base field
[out]	minP	the minimal polynomial of `A`
	N	order of the matrix `A`
[in]	A	the input matrix ( $N \times N$ )
	lda	leading dimension of `A`
	G	a random iterator

◆ MatVecMinPoly()

Polynomial & MatVecMinPoly	(	const Field &	F,
		Polynomial &	minP,
		const size_t	N,
		typename Field::ConstElement_ptr	A,
		const size_t	lda,
		typename Field::ConstElement_ptr	v,
		const size_t	incv
	)

inline

Compute the minimal polynomial of the matrix A and a vector v, namely the first linear dependency relation in the Krylov basis .

Parameters

	F	the base field
[out]	minP	the minimal polynomial of `A` and v
	N	order of the matrix `A`
[in]	A	the input matrix ( $N \times N$ )
	lda	leading dimension of `A`
	K	an 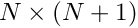$N \times (N+1)$ matrix containing the vector v on its first row
	ldk	leading dimension of `K`
	P	[out] (optional) the permutation used in the elimination of the Krylov matrix `K`

◆ Rank()

size_t Rank	(	const Field &	F,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda
	)

Computes the rank of the given matrix using a PLUQ factorization.

The input matrix is modified.

Parameters

	F	base field
	M	row dimension of the matrix
	N	column dimension of the matrix
[in]	A	input matrix
	lda	leading dimension of A
	psH	(optional) a ParSeqHelper to choose between sequential and parallel execution

◆ IsSingular()

bool IsSingular	(	const Field &	F,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda
	)

Returns true if the given matrix is singular.

The method is a block elimination with early termination

using LQUP factorization with early termination. If M != N, then the matrix is virtually padded with zeros to make it square and it's determinant is zero.

Warning: The input matrix is modified.

Parameters

	F	base field
	M	row dimension of the matrix
	N	column dimension of the matrix.
[in,out]	A	input matrix
	lda	leading dimension of A

◆ Det()

Field::Element & Det	(	const Field &	F,
		typename Field::Element &	det,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *	P = `NULL`,
		size_t *	Q = `NULL`
	)

inline

Returns the determinant of the given square matrix.

The method is a block elimination using PLUQ factorization. The input matrix A is overwritten.

Warning: The input matrix is modified.

Parameters

	F	base field
[out]	det	the determinant of A
	N	the order of the square matrix A.
[in,out]	A	input matrix
	lda	leading dimension of A
	psH	(optional) a ParSeqHelper to choose between sequential and parallel execution
	P,Q	(optional) row and column permutations to be used by the PLUQ factorization. randomized checkers (see cherckes/checker_det.inl) need them for certification

◆ Solve()

Field::Element_ptr Solve	(	const Field &	F,
		const size_t	M,
		typename Field::Element_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	x,
		const int	incx,
		typename Field::ConstElement_ptr	b,
		const int	incb
	)

inline

Solves a linear system AX = b using PLUQ factorization.

@oaram F base field @oaram M matrix order

Parameters

[in]	A	input matrix
	lda	leading dimension of A
[out]	x	output solution vector
	incx	increment of x
	b	input right hand side of the system
	incb	increment of b

◆ RandomNullSpaceVector() [1/2]

*void RandomNullSpaceVector	(	const Field &	F,
		const FFLAS::FFLAS_SIDE	Side,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	X,
		const size_t	incX
	)

Solve L X = B or X L = B in place.

L is M*M if Side == FFLAS::FflasLeft and N*N if Side == FFLAS::FflasRight, B is M*N. Only the R non trivial column of L are stored in the M*R matrix L Requirement : so that L could be expanded in-place Computes a vector of the Left/Right nullspace of the matrix A.

Parameters

	F	The computation domain
	Side	decides whether it computes the left (FflasLeft) or right (FflasRight) nullspace
	M	number of rows
	N	number of columns
[in,out]	A	input matrix of dimension M x N, A is modified to its LU version
	lda	leading dimension of A
[out]	X	output vector
	incX	increment of X

◆ NullSpaceBasis()

size_t NullSpaceBasis	(	const Field &	F,
		const FFLAS::FFLAS_SIDE	Side,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr &	NS,
		size_t &	ldn,
		size_t &	NSdim
	)

Computes a basis of the Left/Right nullspace of the matrix A.

return the dimension of the nullspace.

Parameters

	F	The computation domain
	Side	decides whether it computes the left (FflasLeft) or right (FflasRight) nullspace
	M	number of rows
	N	number of columns
[in,out]	A	input matrix of dimension M x N, A is modified
	lda	leading dimension of A
[out]	NS	output matrix of dimension N x NSdim (allocated here)
[out]	ldn	leading dimension of NS
[out]	NSdim	the dimension of the Nullspace (N-rank(A))

◆ RowRankProfile()

size_t RowRankProfile	(	const Field &	F,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *&	rkprofile,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`
	)

inline

Computes the row rank profile of A.

Parameters

	F	base field
	M	number of rows
	N	number of columns
[in]	A	input matrix of dimension M x N
	lda	leading dimension of A
[out]	rkprofile	return the rank profile as an array of row indexes, of dimension r=rank(A)
	LuTag	chooses the elimination algorithm. SlabRecursive for LUdivine, TileRecursive for PLUQ

A is modified rkprofile is allocated during the computation.

Returns: R

◆ ColumnRankProfile()

size_t ColumnRankProfile	(	const Field &	F,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *&	rkprofile,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`
	)

inline

Computes the column rank profile of A.

Parameters

	F	base field
	M	number of rows
	N	number of columns
[in]	A	input matrix of dimension
	lda	leading dimension of A
[out]	rkprofile	return the rank profile as an array of row indexes, of dimension r=rank(A)
	LuTag	chooses the elimination algorithm. SlabRecursive for LUdivine, TileRecursive for PLUQ

A is modified rkprofile is allocated during the computation.

Returns: R

◆ RankProfileFromLU()

void RankProfileFromLU	(	const size_t *	P,
		const size_t	N,
		const size_t	R,
		size_t *	rkprofile,
		const FFPACK_LU_TAG	LuTag
	)

inline

Recovers the column/row rank profile from the permutation of an LU decomposition.

Works with both the CUP/PLE decompositions (obtained by LUdivine) or the PLUQ decomposition. Assumes that the output vector containing the rank profile is already allocated.

Parameters

	P	the permutation carrying the rank profile information
	N	the row/col dimension for a row/column rank profile
	R	the rank of the matrix
[out]	rkprofile	return the rank profile as an array of indices
	LuTag	chooses the elimination algorithm. SlabRecursive for LUdivine, TileRecursive for PLUQ

◆ LeadingSubmatrixRankProfiles()

size_t LeadingSubmatrixRankProfiles	(	const size_t	M,
		const size_t	N,
		const size_t	R,
		const size_t	LSm,
		const size_t	LSn,
		const size_t *	P,
		const size_t *	Q,
		size_t *	RRP,
		size_t *	CRP
	)

inline

Recovers the row and column rank profiles of any leading submatrix from the PLUQ decomposition.

Only works with the PLUQ decomposition Assumes that the output vectors containing the rank profiles are already allocated.

Parameters

P	the permutation carrying the rank profile information
M	the row dimension of the initial matrix
N	the column dimension of the initial matrix
R	the rank of the initial matrix
LSm	the row dimension of the leading submatrix considered
LSn	the column dimension of the leading submatrix considered
P	the row permutation of the PLUQ decomposition
Q	the column permutation of the PLUQ decomposition
RRP	return the row rank profile of the leading submatrix

Returns: the rank of the LSm x LSn leading submatrix

A is modified

Bibliography:

Dumas J-G., Pernet C., and Sultan Z. Simultaneous computation of the row and column rank profiles , ISSAC'13.

◆ RowRankProfileSubmatrixIndices()

size_t RowRankProfileSubmatrixIndices	(	const Field &	F,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *&	rowindices,
		size_t *&	colindices,
		size_t &	R
	)

RowRankProfileSubmatrixIndices.

Computes the indices of the submatrix r*r X of A whose rows correspond to the row rank profile of A.

Parameters

	F	base field
	M	number of rows
	N	number of columns
[in]	A	input matrix of dimension
	rowindices	array of the row indices of X in A
	colindices	array of the col indices of X in A
	lda	leading dimension of A
[out]	R	list of indices

rowindices and colindices are allocated during the computation. A is modified

Returns: R

◆ ColRankProfileSubmatrixIndices()

size_t ColRankProfileSubmatrixIndices	(	const Field &	F,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *&	rowindices,
		size_t *&	colindices,
		size_t &	R
	)

Computes the indices of the submatrix r*r X of A whose columns correspond to the column rank profile of A.

Parameters

	F	base field
	M	number of rows
	N	number of columns
[in]	A	input matrix of dimension
	rowindices	array of the row indices of X in A
	colindices	array of the col indices of X in A
	lda	leading dimension of A
[out]	R	list of indices

rowindices and colindices are allocated during the computation.

Warning: A is modified

Returns: R

◆ RowRankProfileSubmatrix()

size_t RowRankProfileSubmatrix	(	const Field &	F,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr &	X,
		size_t &	R
	)

Computes the r*r submatrix X of A, by picking the row rank profile rows of A.

Parameters

	F	base field
	M	number of rows
	N	number of columns
[in]	A	input matrix of dimension M x N
	lda	leading dimension of A
[out]	X	the output matrix
[out]	R	list of indices

A is not modified X is allocated during the computation.

Returns: R

◆ ColRankProfileSubmatrix()

size_t ColRankProfileSubmatrix	(	const Field &	F,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr &	X,
		size_t &	R
	)

Compute the $r\times r$ submatrix X of A, by picking the row rank profile rows of A.

Parameters

	F	base field
	M	number of rows
	N	number of columns
[in]	A	input matrix of dimension M x N
	lda	leading dimension of A
[out]	X	the output matrix
[out]	R	list of indices

A is not modified X is allocated during the computation.

Returns: R

◆ getTriangular() [1/2]

void getTriangular	(	const Field &	F,
		const FFLAS::FFLAS_UPLO	Uplo,
		const FFLAS::FFLAS_DIAG	diag,
		const size_t	M,
		const size_t	N,
		const size_t	R,
		typename Field::ConstElement_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	T,
		const size_t	ldt,
		const bool	OnlyNonZeroVectors = `false`
	)

inline

Extracts a triangular matrix from a compact storage A=L\U of rank R.

if OnlyNonZeroVectors is false, then T and A have the same dimensions Otherwise, T is R x N if UpLo = FflasUpper, else T is M x R

Parameters

	F	base field
	UpLo	selects if the upper (FflasUpper) or lower (FflasLower) triangular matrix is returned
	diag	selects if the triangular matrix unit-diagonal (FflasUnit/NoUnit)
	M	row dimension of T
	N	column dimension of T
	R	rank of the triangular matrix (how many rows/columns need to be copied)
[in]	A	input matrix
	lda	leading dimension of A
[out]	T	output matrix
	ldt	leading dimension of T
	OnlyNonZeroVectors	decides whether the last zero rows/columns should be ignored

Todo:: just one triangular fzero+fassign ?

Todo:: just one triangular fzero+fassign ?

◆ getTriangular() [2/2]

void getTriangular	(	const Field &	F,
		const FFLAS::FFLAS_UPLO	Uplo,
		const FFLAS::FFLAS_DIAG	diag,
		const size_t	M,
		const size_t	N,
		const size_t	R,
		typename Field::Element_ptr	A,
		const size_t	lda
	)

inline

Cleans up a compact storage A=L\U to reveal a triangular matrix of rank R.

Parameters

	F	base field
	UpLo	selects if the upper (FflasUpper) or lower (FflasLower) triangular matrix is revealed
	diag	selects if the triangular matrix unit-diagonal (FflasUnit/NoUnit)
	M	row dimension of A
	N	column dimension of A
	R	rank of the triangular matrix
[in,out]	A	input/output matrix
	lda	leading dimension of A

Todo:: just one triangular fzero+fassign ?

Todo:: just one triangular fzero+fassign ?

◆ getEchelonForm() [1/2]

void getEchelonForm	(	const Field &	F,
		const FFLAS::FFLAS_UPLO	Uplo,
		const FFLAS::FFLAS_DIAG	diag,
		const size_t	M,
		const size_t	N,
		const size_t	R,
		const size_t *	P,
		typename Field::ConstElement_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	T,
		const size_t	ldt,
		const bool	OnlyNonZeroVectors = `false`,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`
	)

inline

Extracts a matrix in echelon form from a compact storage A=L\U of rank R obtained by RowEchelonForm or ColumnEchelonForm.

Either L or U is in Echelon form (depending on Uplo) The echelon structure is defined by the first R values of the array P. row and column dimension of T are greater or equal to that of A

Parameters

	F	base field
	UpLo	selects if the upper (FflasUpper) or lower (FflasLower) triangular matrix is returned
	diag	selects if the echelon matrix has unit pivots (FflasUnit/NoUnit)
	M	row dimension of T
	N	column dimension of T
	R	rank of the triangular matrix (how many rows/columns need to be copied)
	P	positions of the R pivots
[in]	A	input matrix
	lda	leading dimension of A
[out]	T	output matrix
	ldt	leading dimension of T
	OnlyNonZeroVectors	decides whether the last zero rows/columns should be ignored
	LuTag	which factorized form (CUP/PLE if FfpackSlabRecursive, PLUQ if FfpackTileRecursive)

◆ getEchelonForm() [2/2]

void getEchelonForm	(	const Field &	F,
		const FFLAS::FFLAS_UPLO	Uplo,
		const FFLAS::FFLAS_DIAG	diag,
		const size_t	M,
		const size_t	N,
		const size_t	R,
		const size_t *	P,
		typename Field::Element_ptr	A,
		const size_t	lda,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`
	)

inline

Cleans up a compact storage A=L\U obtained by RowEchelonForm or ColumnEchelonForm to reveal an echelon form of rank R.

Either L or U is in Echelon form (depending on Uplo) The echelon structure is defined by the first R values of the array P.

Parameters

	F	base field
	UpLo	selects if the upper (FflasUpper) or lower (FflasLower) triangular matrix is returned
	diag	selects if the echelon matrix has unit pivots (FflasUnit/NoUnit)
	M	row dimension of A
	N	column dimension of A
	R	rank of the triangular matrix (how many rows/columns need to be copied)
	P	positions of the R pivots
[in,out]	A	input/output matrix
	lda	leading dimension of A
	LuTag	which factorized form (CUP/PLE if FfpackSlabRecursive, PLUQ if FfpackTileRecursive)

◆ getEchelonTransform()

void getEchelonTransform	(	const Field &	F,
		const FFLAS::FFLAS_UPLO	Uplo,
		const FFLAS::FFLAS_DIAG	diag,
		const size_t	M,
		const size_t	N,
		const size_t	R,
		const size_t *	P,
		const size_t *	Q,
		typename Field::ConstElement_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	T,
		const size_t	ldt,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`
	)

inline

Extracts a transformation matrix to echelon form from a compact storage A=L\U of rank R obtained by RowEchelonForm or ColumnEchelonForm.

If Uplo == FflasLower: T is N x N (already allocated) such that A T = C is a transformation of A in Column echelon form Else T is M x M (already allocated) such that T A = E is a transformation of A in Row Echelon form

Parameters

	F	base field
	UpLo	Lower (FflasLower) means Transformation to Column Echelon Form, Upper (FflasUpper), to Row Echelon Form
	diag	selects if the echelon matrix has unit pivots (FflasUnit/NoUnit)
	M	row dimension of A
	N	column dimension of A
	R	rank of the triangular matrix
	P	permutation matrix
[in]	A	input matrix
	lda	leading dimension of A
[out]	T	output matrix
	ldt	leading dimension of T
	LuTag	which factorized form (CUP/PLE if FfpackSlabRecursive, PLUQ if FfpackTileRecursive)

◆ getReducedEchelonForm() [1/2]

void getReducedEchelonForm	(	const Field &	F,
		const FFLAS::FFLAS_UPLO	Uplo,
		const size_t	M,
		const size_t	N,
		const size_t	R,
		const size_t *	P,
		typename Field::ConstElement_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	T,
		const size_t	ldt,
		const bool	OnlyNonZeroVectors = `false`,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`
	)

inline

Extracts a matrix in echelon form from a compact storage A=L\U of rank R obtained by ReducedRowEchelonForm or ReducedColumnEchelonForm with transform = true.

Either L or U is in Echelon form (depending on Uplo) The echelon structure is defined by the first R values of the array P. row and column dimension of T are greater or equal to that of A

Parameters

	F	base field
	UpLo	selects if the upper (FflasUpper) or lower (FflasLower) triangular matrix is returned
	diag	selects if the echelon matrix has unit pivots (FflasUnit/NoUnit)
	M	row dimension of T
	N	column dimension of T
	R	rank of the triangular matrix (how many rows/columns need to be copied)
	P	positions of the R pivots
[in]	A	input matrix
	lda	leading dimension of A
	ldt	leading dimension of T
	LuTag	which factorized form (CUP/PLE if FfpackSlabRecursive, PLUQ if FfpackTileRecursive)
	OnlyNonZeroVectors	decides whether the last zero rows/columns should be ignored

◆ getReducedEchelonForm() [2/2]

void getReducedEchelonForm	(	const Field &	F,
		const FFLAS::FFLAS_UPLO	Uplo,
		const size_t	M,
		const size_t	N,
		const size_t	R,
		const size_t *	P,
		typename Field::Element_ptr	A,
		const size_t	lda,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`
	)

inline

Cleans up a compact storage A=L\U of rank R obtained by ReducedRowEchelonForm or ReducedColumnEchelonForm with transform = true.

Either L or U is in Echelon form (depending on Uplo) The echelon structure is defined by the first R values of the array P.

Parameters

	F	base field
	UpLo	selects if the upper (FflasUpper) or lower (FflasLower) triangular matrix is returned
	diag	selects if the echelon matrix has unit pivots (FflasUnit/NoUnit)
	M	row dimension of A
	N	column dimension of A
	R	rank of the triangular matrix (how many rows/columns need to be copied)
	P	positions of the R pivots
[in,out]	A	input/output matrix
	lda	leading dimension of A
	LuTag	which factorized form (CUP/PLE if FfpackSlabRecursive, PLUQ if FfpackTileRecursive)

◆ getReducedEchelonTransform()

void getReducedEchelonTransform	(	const Field &	F,
		const FFLAS::FFLAS_UPLO	Uplo,
		const size_t	M,
		const size_t	N,
		const size_t	R,
		const size_t *	P,
		const size_t *	Q,
		typename Field::ConstElement_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	T,
		const size_t	ldt,
		const FFPACK_LU_TAG	LuTag = `FfpackSlabRecursive`
	)

inline

Extracts a transformation matrix to echelon form from a compact storage A=L\U of rank R obtained by RowEchelonForm or ColumnEchelonForm.

If Uplo == FflasLower: T is N x N (already allocated) such that A T = C is a transformation of A in Column echelon form Else T is M x M (already allocated) such that T A = E is a transformation of A in Row Echelon form

Parameters

	F	base field
	UpLo	selects Col (FflasLower) or Row (FflasUpper) Echelon Form
	diag	selects if the echelon matrix has unit pivots (FflasUnit/NoUnit)
	M	row dimension of A
	N	column dimension of A
	R	rank of the triangular matrix
	P	permutation matrix
[in]	A	input matrix
	lda	leading dimension of A
[out]	T	output matrix
	ldt	leading dimension of T
	LuTag	which factorized form (CUP/PLE if FfpackSlabRecursive, PLUQ if FfpackTileRecursive)

◆ LTBruhatGen()

size_t LTBruhatGen	(	const Field &	Fi,
		const FFLAS::FFLAS_DIAG	diag,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *	P,
		size_t *	Q
	)

inline

LTBruhatGen Suppose A is Left Triangular Matrix This procedure computes the Bruhat Representation of A and return the rank of A.

Parameters

Fi	base Field
diag
N	size of A
A	the matrix we search the Bruhat representation
lda	the leading dimension of A
P	a permutation matrix
Q	a permutation matrix

◆ getLTBruhatGen() [1/2]

void getLTBruhatGen	(	const Field &	Fi,
		const size_t	N,
		const size_t	r,
		const size_t *	P,
		const size_t *	Q,
		typename Field::Element_ptr	R,
		const size_t	ldr
	)

inline

GetLTBruhatGen This procedure Computes the Rank Revealing Matrix based on the Bruhta representation of a Matrix.

Parameters

Fi	base Field
N	size of the matrix
r	the rank of the matrix
P	a permutation matrix
Q	a permutation matrix
R	the matrix that will contain the rank revealing matrix
ldr	the leading fimension of R

◆ getLTBruhatGen() [2/2]

void getLTBruhatGen	(	const Field &	Fi,
		const FFLAS::FFLAS_UPLO	Uplo,
		const FFLAS::FFLAS_DIAG	diag,
		const size_t	N,
		const size_t	r,
		const size_t *	P,
		const size_t *	Q,
		typename Field::ConstElement_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	T,
		const size_t	ldt
	)

inline

GetLTBruhatGen This procedure computes the matrix L or U f the Bruhat Representation Suppose that A is the bruhat representation of a matrix.

Parameters

Fi	base Field
Uplo	choose if the procedure return L or U
diag
N	size of A
r	rank of A
P	permutaion matrix
Q	permutation matrix
A	a bruhat representation
lda	leading dimension of A
T	matrix that will contains L or U
ldt	leading dimension of T

◆ LTQSorder()

size_t LTQSorder	(	const size_t	N,
		const size_t	r,
		const size_t *	P,
		const size_t *	Q
	)

inline

LTQSorder This procedure computes the order of quasiseparability of a matrix.

Parameters

N	size of the matrix
r	rank of the matrix
P	permutation matrix
Q	permutation matrix

◆ CompressToBlockBiDiagonal()

size_t CompressToBlockBiDiagonal	(	const Field &	Fi,
		const FFLAS::FFLAS_UPLO	Uplo,
		size_t	N,
		size_t	s,
		size_t	r,
		const size_t *	P,
		const size_t *	Q,
		typename Field::Element_ptr	A,
		size_t	lda,
		typename Field::Element_ptr	X,
		size_t	ldx,
		size_t *	K,
		size_t *	M,
		size_t *	T
	)

inline

CompressToBlockBiDiagonal This procedure compress a compact representation of a row echelon form or column echelon form.

Parameters

Fi	base Field
Uplo	chosse if the procedure is based on row or column
N	size of the matrix
s	order of qausiseparability
r	rank
P	permutation matrix
Q	permutation matrix
A	the matrix to compact
lda	leading dimension of A
X	matrix that will stock the representation
ldx	leading dimension of X
K	stock the position of the blocks in A
M	permutation matrix
T	stock the operation done in the procedure

◆ ExpandBlockBiDiagonalToBruhat()

void ExpandBlockBiDiagonalToBruhat	(	const Field &	Fi,
		const FFLAS::FFLAS_UPLO	Uplo,
		size_t	N,
		size_t	s,
		size_t	r,
		typename Field::Element_ptr	A,
		size_t	lda,
		typename Field::Element_ptr	X,
		size_t	ldx,
		size_t	NbBlocks,
		size_t *	K,
		size_t *	M,
		size_t *	T
	)

inline

ExpandBlockBiDiagonal This procedure expand a compact representation of a row echelon form or column echelon form.

Parameters

Fi	base Field
Uplo	chosse if the procedure is based on row or column
N	size of the matrix
s	order of qausiseparability
r	rank
A	the matrix that will sotck the expanded representation
lda	leading dimension of A
X	matrix to expand
ldx	leading dimension of X
K	stock the position of the blocks in A
M	permutation matrix
T	stock the operation done in the procedure

◆ Bruhat2EchelonPermutation()

void Bruhat2EchelonPermutation	(	size_t	N,
		size_t	R,
		const size_t *	P,
		const size_t *	Q,
		size_t *	M
	)

inline

Bruhat2EchelonPermutation (N,R,P,Q) Compute M such that LM or MU is in echelon form where L or U are factors of the Bruhat Rpresentation.

Parameters

[in]	N	size of the matrix
[in]	R	rank
[in]	P	permutation Matrix
[in]	Q	permutation Matrix
[out]	M	output permutation matrix

◆ LQUPtoInverseOfFullRankMinor()

Field::Element_ptr LQUPtoInverseOfFullRankMinor	(	const Field &	F,
		const size_t	rank,
		typename Field::Element_ptr	A_factors,
		const size_t	lda,
		const size_t *	QtPointer,
		typename Field::Element_ptr	X,
		const size_t	ldx
	)

LQUPtoInverseOfFullRankMinor.

Suppose A has been factorized as L.Q.U.P, with rank r. Then Qt.A.Pt has an invertible leading principal r x r submatrix This procedure efficiently computes the inverse of this minor and puts it into X.

Note: It changes the lower entries of A_factors in the process (NB: unless A was nonsingular and square)

Parameters

F	base field
rank	rank of the matrix.
A_factors	matrix containing the L and U entries of the factorization
lda	leading dimension of A
QtPointer	theLQUP->getQ()->getPointer() (note: getQ returns Qt!)
X	desired location for output
ldx	leading dimension of X

◆ RandomNullSpaceVector() [2/2]

void RandomNullSpaceVector	(	const Field &	F,
		const FFLAS::FFLAS_SIDE	Side,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	X,
		const size_t	incX
	)

Solve L X = B or X L = B in place.

L is M*M if Side == FFLAS::FflasLeft and N*N if Side == FFLAS::FflasRight, B is M*N. Only the R non trivial column of L are stored in the M*R matrix L Requirement : so that L could be expanded in-place Computes a vector of the Left/Right nullspace of the matrix A.

Parameters

	F	The computation domain
	Side	decides whether it computes the left (FflasLeft) or right (FflasRight) nullspace
	M	number of rows
	N	number of columns
[in,out]	A	input matrix of dimension M x N, A is modified to its LU version
	lda	leading dimension of A
[out]	X	output vector
	incX	increment of X

◆ productBruhatxTS()

void productBruhatxTS	(	const Field &	Fi,
		size_t	N,
		size_t	s,
		size_t	r,
		size_t	t,
		const size_t *	P,
		const size_t *	Q,
		typename Field::ConstElement_ptr	Xu,
		size_t	ldu,
		size_t	NbBlocksU,
		const size_t *	Ku,
		const size_t *	Tu,
		const size_t *	MU,
		typename Field::ConstElement_ptr	Xl,
		size_t	ldl,
		size_t	NbBlocksL,
		const size_t *	Kl,
		const size_t *	Tl,
		const size_t *	ML,
		typename Field::Element_ptr	B,
		size_t	ldb,
		const typename Field::Element	beta,
		typename Field::Element_ptr	D,
		size_t	ldd
	)

inline

Compute the product of a left-triangular quasi-separable matrix A, represented by a compact Bruhat generator, with a dense rectangular matrix B: $C \gets A \times B + beta C$ .

Parameters

	F	the base field
	N	the order of `A`
	s	the order of quasiseparability of `A`
	r	the number of pivots in the left-triangular par of the rank profile matrix of `A`
	t	the number of columns of `B`
	P	the row indices of the pivots of `A`
	Q	the column indices of the pivots of `A`
	Xu	the compact storage of U: Du blocks in the first s rows, Su blocks in the last s rows
	ldxu	the leading dimension of `Xu`
	NbBlocksU	the number of diagonal blocks in the compact storage of U
	Ku	the list of starting column positions for each block of the storage of U
	Tu	the folding matrix for the compact storage of U: 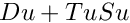is in row echelon form
	Mu	a permutation matrix such that 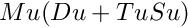is the U factor of the Bruhat generator
	Xl	the compact storage of L: Dl blocks in the first s columns, Sl blocks in the last s columns
	ldxl	the leading dimension of `Xl`
	NbBlocksL	the number of diagonal blocks in the compact storage of L
	Kl	the list of starting row positions for each block of the storage of L
	Tl	the folding matrix for the compact storage of L: 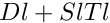is in column echelon form
	Ml	a permutation matrix such that 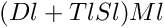is the L factor of the Bruhat generator
	B	an $N \times t$ dense matrix
	ldb	leading dimension of `B`
	beta	scaling constant
[in,out]	C	output matrix
	ldc	leading dimension of `C`

Bibliography:: Pernet C. and Storjohann A. Time and space efficient generators for quasiseparable matrices , JSC (85), 2018, doi:10.1016/j.jsc.2017.07.010

◆ buildMatrix()

Field::Element_ptr buildMatrix	(	const Field &	F,
		typename Field::ConstElement_ptr	E,
		typename Field::ConstElement_ptr	C,
		const size_t	lda,
		const size_t *	B,
		const size_t *	T,
		const size_t	me,
		const size_t	mc,
		const size_t	lambda,
		const size_t	mu
	)

Bug:: is this :

◆ fsytrf_UP_RPM()

size_t fsytrf_UP_RPM	(	const Field &	Fi,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		typename Field::Element_ptr	Dinv,
		const size_t	incDinv,
		size_t *	P,
		size_t	BCThreshold
	)

inline

MathP <-[ [ I ] x P1 | ] [ I_(N1+R2) ] [ P2^T ] | ] x [ P3^T ] [ -----------—|--— ] [ | Q2^T ]

Changing [ U1 V1 | E1 E21 E22 ] into [ U1 E11 E12 V1 E* E* ] [ 0 | L2 \ U2 V21 V22 ] [ U4 V41 0 V42 V43 ] [ 0 | M2 0 0 ] [ U3 0 0 V3 ] [ ---—|-------------— ] [ 0 0 0 ] [ 0 | H1 H21 H22 ] [ 0 | U3 V3 ] [ 0 | 0 ] where U4 is the 2R2 x 2R2 matrix formed by interleaving U2, L2^T and H1

◆ LUdivine() [2/2]

size_t LUdivine	(	const Field &	F,
		const FFLAS::FFLAS_DIAG	Diag,
		const FFLAS::FFLAS_TRANSPOSE	trans,
		const size_t	M,
		const size_t	N,
		typename Field::Element_ptr	A,
		const size_t	lda,
		size_t *	P,
		size_t *	Q,
		const FFPACK::FFPACK_LU_TAG	LuTag,
		const size_t	cutoff
	)

inline

Todo:: std::swap ?

◆ composePermutationsLLL()

void composePermutationsLLL	(	size_t *	P1,
		const size_t *	P2,
		const size_t	R,
		const size_t	N
	)

inline

Computes P1 x Diag (I_R, P2) where P1 is a LAPACK and P2 a LAPACK permutation and store the result in P1 as a LAPACK permutation.

Parameters

[in,out]	P1	a LAPACK permutation of size N
	P2	a LAPACK permutation of size N-R

◆ composePermutationsLLM()

void composePermutationsLLM	(	size_t *	MathP,
		const size_t *	P1,
		const size_t *	P2,
		const size_t	R,
		const size_t	N
	)

inline

Computes P1 x Diag (I_R, P2) where P1 is a LAPACK and P2 a LAPACK permutation and store the result in MathP as a MathPermutation format.

Parameters

[out]

a MathPermutation of size N

Parameters

P1	a LAPACK permutation of size N
P2	a LAPACK permutation of size N-R

◆ composePermutationsMLM()

void composePermutationsMLM	(	size_t *	MathP1,
		const size_t *	P2,
		const size_t	R,
		const size_t	N
	)

inline

Computes MathP1 x Diag (I_R, P2) where MathP1 is a MathPermutation and P2 a LAPACK permutation and store the result in MathP1 as a MathPermutation format.

Parameters

[in,out]	MathP1	a MathPermutation of size N
	P2	a LAPACK permutation of size N-R

◆ NonZeroRandomMatrix() [1/2]

Field::Element_ptr NonZeroRandomMatrix	(	const Field &	F,
		size_t	m,
		size_t	n,
		typename Field::Element_ptr	A,
		size_t	lda,
		RandIter &	G
	)

inline

Random non-zero Matrix.

Creates a m x n matrix with random entries, and at least one of them is non zero.

Parameters

	F	field
	m	number of rows in `A`
	n	number of cols in `A`
[out]	A	the matrix (preallocated to at least `m` x `lda` field elements)
	lda	leading dimension of `A`
	G	a random iterator

Returns: A.

◆ NonZeroRandomMatrix() [2/2]

Field::Element_ptr NonZeroRandomMatrix	(	const Field &	F,
		size_t	m,
		size_t	n,
		typename Field::Element_ptr	A,
		size_t	lda
	)

inline

Random non-zero Matrix.

Creates a m x n matrix with random entries, and at least one of them is non zero.

Parameters

	F	field
	m	number of rows in `A`
	n	number of cols in `A`
[out]	A	the matrix (preallocated to at least `m` x `lda` field elements)
	lda	leading dimension of `A`

Returns: A.

◆ RandomMatrix() [1/2]

Field::Element_ptr RandomMatrix	(	const Field &	F,
		size_t	m,
		size_t	n,
		typename Field::Element_ptr	A,
		size_t	lda,
		RandIter &	G
	)

inline

Random Matrix.

Creates a m x n matrix with random entries.

Parameters

	F	field
	m	number of rows in `A`
	n	number of cols in `A`
[out]	A	the matrix (preallocated to at least `m` x `lda` field elements)
	lda	leading dimension of `A`
	G	a random iterator

Returns: A.

◆ RandomMatrix() [2/2]

Field::Element_ptr RandomMatrix	(	const Field &	F,
		size_t	m,
		size_t	n,
		typename Field::Element_ptr	A,
		size_t	lda
	)

inline

Random Matrix.

Creates a m x n matrix with random entries.

Parameters

	F	field
	m	number of rows in `A`
	n	number of cols in `A`
[out]	A	the matrix (preallocated to at least `m` x `lda` field elements)
	lda	leading dimension of `A`

Returns: A.

◆ RandomTriangularMatrix() [1/2]

Field::Element_ptr RandomTriangularMatrix	(	const Field &	F,
		size_t	m,
		size_t	n,
		const FFLAS::FFLAS_UPLO	UpLo,
		const FFLAS::FFLAS_DIAG	Diag,
		bool	nonsingular,
		typename Field::Element_ptr	A,
		size_t	lda,
		RandIter &	G
	)

inline

Random Triangular Matrix.

Creates a m x n triangular matrix with random entries. The UpLo parameter defines wether it is upper or lower triangular.

Parameters

	F	field
	m	number of rows in `A`
	n	number of cols in `A`
	UpLo	whether `A` is upper or lower triangular
[out]	A	the matrix (preallocated to at least `m` x `lda` field elements)
	lda	leading dimension of `A`
	G	a random iterator

Returns: A.

◆ RandomTriangularMatrix() [2/2]

Field::Element_ptr RandomTriangularMatrix	(	const Field &	F,
		size_t	m,
		size_t	n,
		const FFLAS::FFLAS_UPLO	UpLo,
		const FFLAS::FFLAS_DIAG	Diag,
		bool	nonsingular,
		typename Field::Element_ptr	A,
		size_t	lda
	)

inline

Random Triangular Matrix.

Creates a m x n triangular matrix with random entries. The UpLo parameter defines wether it is upper or lower triangular.

Parameters

	F	field
	m	number of rows in `A`
	n	number of cols in `A`
	UpLo	whether `A` is upper or lower triangular
[out]	A	the matrix (preallocated to at least `m` x `lda` field elements)
	lda	leading dimension of `A`

Returns: A.

◆ RandomSymmetricMatrix()

Field::Element_ptr RandomSymmetricMatrix	(	const Field &	F,
		size_t	n,
		bool	nonsingular,
		typename Field::Element_ptr	A,
		size_t	lda,
		RandIter &	G
	)

inline

Random Symmetric Matrix.

Creates a m x n triangular matrix with random entries. The UpLo parameter defines wether it is upper or lower triangular.

Parameters

	F	field
	n	order of `A`
[out]	A	the matrix (preallocated to at least `n` x `lda` field elements)
	lda	leading dimension of `A`
	G	a random iterator

Returns: A.

◆ RandomMatrixWithRank() [1/2]

Field::Element_ptr RandomMatrixWithRank	(	const Field &	F,
		size_t	m,
		size_t	n,
		size_t	r,
		typename Field::Element_ptr	A,
		size_t	lda,
		RandIter &	G
	)

inline

Random Matrix with prescribed rank.

Creates an m x n matrix with random entries and rank r.

Parameters

F	field
m	number of rows in `A`
n	number of cols in `A`
r	rank of the matrix to build
A	the matrix (preallocated to at least `m` x `lda` field elements)
lda	leading dimension of `A`
G	a random iterator

Returns: A.

◆ RandomMatrixWithRank() [2/2]

Field::Element_ptr RandomMatrixWithRank	(	const Field &	F,
		size_t	m,
		size_t	n,
		size_t	r,
		typename Field::Element_ptr	A,
		size_t	lda
	)

inline

Random Matrix with prescribed rank.

Creates an m x n matrix with random entries and rank r.

Parameters

	F	field
	m	number of rows in `A`
	n	number of cols in `A`
	r	rank of the matrix to build
[out]	A	the matrix (preallocated to at least `m` x `lda` field elements)
	lda	leading dimension of `A`

Returns: A.

◆ RandomIndexSubset()

size_t * RandomIndexSubset	(	size_t	N,
		size_t	R,
		size_t *	P
	)

inline

Pick uniformly at random a sequence of R distinct elements from the set $\{0,\dots, N-1\}$ using Knuth's shuffle.

Parameters

	N	the cardinality of the sampling set
	R	the number of elements to sample
[out]	P	the output sequence (pre-allocated to at least R indices)

◆ RandomPermutation()

size_t * RandomPermutation	(	size_t	N,
		size_t *	P
	)

inline

Pick uniformly at random a permutation of size N stored in LAPACK format using Knuth's shuffle.

Parameters

	N	the length of the permutation
[out]	P	the output permutation (pre-allocated to at least N indices)

◆ RandomRankProfileMatrix()

void RandomRankProfileMatrix	(	size_t	M,
		size_t	N,
		size_t	R,
		size_t *	rows,
		size_t *	cols
	)

inline

Pick uniformly at random an R-subpermutation of dimension M x N : a matrix with only R non-zeros equal to one, in a random rook placement.

Parameters

	M	row dimension
	N	column dimension
[out]	rows	the row position of each non zero element (pre-allocated)
[out]	cols	the column position of each non zero element (pre-allocated)

◆ RandomSymmetricRankProfileMatrix()

void RandomSymmetricRankProfileMatrix	(	size_t	N,
		size_t	R,
		size_t *	rows,
		size_t *	cols
	)

inline

Pick uniformly at random a symmetric R-subpermutation of dimension N x N : a symmetric matrix with only R non-zeros, all equal to one, in a random rook placement.

Parameters

	N	matrix order
[out]	rows	the row position of each non zero element (pre-allocated)
[out]	cols	the column position of each non zero element (pre-allocated)

◆ RandomMatrixWithRankandRPM() [1/2]

Field::Element_ptr RandomMatrixWithRankandRPM	(	const Field &	F,
		size_t	M,
		size_t	N,
		size_t	R,
		typename Field::Element_ptr	A,
		size_t	lda,
		const size_t *	RRP,
		const size_t *	CRP,
		RandIter &	G
	)

inline

Random Matrix with prescribed rank and rank profile matrix Creates an m x n matrix with random entries and rank r.

Parameters

F	field
m	number of rows in `A`
n	number of cols in `A`
r	rank of the matrix to build
A	the matrix (preallocated to at least `m` x `lda` field elements)
lda	leading dimension of `A`
RRP	the R dimensional array with row positions of the rank profile matrix' pivots
CRP	the R dimensional array with column positions of the rank profile matrix' pivots
G	a random iterator

Returns: A.

◆ RandomMatrixWithRankandRPM() [2/2]

Field::Element_ptr RandomMatrixWithRankandRPM	(	const Field &	F,
		size_t	M,
		size_t	N,
		size_t	R,
		typename Field::Element_ptr	A,
		size_t	lda,
		const size_t *	RRP,
		const size_t *	CRP
	)

inline

Random Matrix with prescribed rank and rank profile matrix Creates an m x n matrix with random entries and rank r.

Parameters

F	field
m	number of rows in `A`
n	number of cols in `A`
r	rank of the matrix to build
A	the matrix (preallocated to at least `m` x `lda` field elements)
lda	leading dimension of `A`
RRP	the R dimensional array with row positions of the rank profile matrix' pivots
CRP	the R dimensional array with column positions of the rank profile matrix' pivots

Returns: A.

◆ RandomSymmetricMatrixWithRankandRPM() [1/2]

Field::Element_ptr RandomSymmetricMatrixWithRankandRPM	(	const Field &	F,
		size_t	N,
		size_t	R,
		typename Field::Element_ptr	A,
		size_t	lda,
		const size_t *	RRP,
		const size_t *	CRP,
		RandIter &	G
	)

inline

Random Symmetric Matrix with prescribed rank and rank profile matrix Creates an n x n symmetric matrix with random entries and rank r.

Parameters

F	field
n	order of `A`
r	rank of `A`
A	the matrix (preallocated to at least `n` x `lda` field elements)
lda	leading dimension of `A`
RRP	the R dimensional array with row positions of the rank profile matrix' pivots
CRP	the R dimensional array with column positions of the rank profile matrix' pivots
G	a random iterator

Returns: A.

◆ RandomSymmetricMatrixWithRankandRPM() [2/2]

Field::Element_ptr RandomSymmetricMatrixWithRankandRPM	(	const Field &	F,
		size_t	M,
		size_t	N,
		size_t	R,
		typename Field::Element_ptr	A,
		size_t	lda,
		const size_t *	RRP,
		const size_t *	CRP
	)

inline

Random Symmetric Matrix with prescribed rank and rank profile matrix Creates an n x n symmetric matrix with random entries and rank r.

Parameters

F	field
n	order of `A`
r	rank of `A`
A	the matrix (preallocated to at least `n` x `lda` field elements)
lda	leading dimension of `A`
RRP	the R dimensional array with row positions of the rank profile matrix' pivots
CRP	the R dimensional array with column positions of the rank profile matrix' pivots

Returns: A.

◆ RandomMatrixWithRankandRandomRPM() [1/2]

Field::Element_ptr RandomMatrixWithRankandRandomRPM	(	const Field &	F,
		size_t	M,
		size_t	N,
		size_t	R,
		typename Field::Element_ptr	A,
		size_t	lda,
		RandIter &	G
	)

inline

Random Matrix with prescribed rank, with random rank profile matrix Creates an m x n matrix with random entries, rank r and with a rank profile matrix chosen uniformly at random.

Parameters

F	field
m	number of rows in `A`
n	number of cols in `A`
r	rank of the matrix to build
A	the matrix (preallocated to at least `m` x `lda` field elements)
lda	leading dimension of `A`
G	a random iterator

Returns: A.

◆ RandomMatrixWithRankandRandomRPM() [2/2]

Field::Element_ptr RandomMatrixWithRankandRandomRPM	(	const Field &	F,
		size_t	M,
		size_t	N,
		size_t	R,
		typename Field::Element_ptr	A,
		size_t	lda
	)

inline

Random Matrix with prescribed rank, with random rank profile matrix Creates an m x n matrix with random entries, rank r and with a rank profile matrix chosen uniformly at random.

Parameters

F	field
m	number of rows in `A`
n	number of cols in `A`
r	rank of the matrix to build
A	the matrix (preallocated to at least `m` x `lda` field elements)
lda	leading dimension of `A`

Returns: A.

◆ RandomSymmetricMatrixWithRankandRandomRPM() [1/2]

Field::Element_ptr RandomSymmetricMatrixWithRankandRandomRPM	(	const Field &	F,
		size_t	N,
		size_t	R,
		typename Field::Element_ptr	A,
		size_t	lda,
		RandIter &	G
	)

inline

Random Symmetric Matrix with prescribed rank, with random rank profile matrix Creates an n x n matrix with random entries, rank r and with a rank profile matrix chosen uniformly at random.

Parameters

F	field
n	order of `A`
r	rank of `A`
A	the matrix (preallocated to at least `n` x `lda` field elements)
lda	leading dimension of `A`
G	a random iterator

Returns: A.

◆ RandomSymmetricMatrixWithRankandRandomRPM() [2/2]

Field::Element_ptr RandomSymmetricMatrixWithRankandRandomRPM	(	const Field &	F,
		size_t	N,
		size_t	R,
		typename Field::Element_ptr	A,
		size_t	lda
	)

inline

Random Symmetric Matrix with prescribed rank, with random rank profile matrix Creates an n x n matrix with random entries, rank r and with a rank profile matrix chosen uniformly at random.

Parameters

F	field
n	order of `A`
r	rank of `A`
A	the matrix (preallocated to at least `n` x `lda` field elements)
lda	leading dimension of `A`

Returns: A.

◆ RandomMatrixWithDet() [1/2]

Field::Element_ptr RandomMatrixWithDet	(	const Field &	F,
		size_t	n,
		const typename Field::Element	d,
		typename Field::Element_ptr	A,
		size_t	lda
	)

inline

Random Matrix with prescribed det.

Creates a m x n matrix with random entries and rank r.

Parameters

F	field
d	the prescribed value for the determinant of A
n	number of cols in `A`
A	the matrix to be generated (preallocated to at least `n` x `lda` field elements)
lda	leading dimension of `A`

Returns: A.

◆ RandomMatrixWithDet() [2/2]

Field::Element_ptr RandomMatrixWithDet	(	const Field &	F,
		size_t	n,
		const typename Field::Element	d,
		typename Field::Element_ptr	A,
		size_t	lda,
		RandIter &	G
	)

inline

Random Matrix with prescribed det.

Creates a m x n matrix with random entries and rank r.

Parameters

F	field
d	the prescribed value for the determinant of A
n	number of cols in `A`
A	the matrix to be generated (preallocated to at least `n` x `lda` field elements)
lda	leading dimension of `A`

Returns: A.

Data Structures

Functions

Detailed Description

Function Documentation

◆ applyP()

◆ MonotonicApplyP()

◆ fgetrs() [1/2]

◆ fgetrs() [2/2]

◆ fgesv() [1/2]

◆ fgesv() [2/2]

◆ ftrtri()

◆ ftrtrm()

◆ ftrstr()

◆ ftrssyr2k()

◆ fsytrf()

◆ fsytrf_nonunit()

◆ PLUQ()

◆ LUdivine() [1/2]

◆ ColumnEchelonForm()

◆ RowEchelonForm()

◆ ReducedColumnEchelonForm()

◆ ReducedRowEchelonForm()

◆ Invert() [1/2]

◆ Invert() [2/2]

◆ Invert2()

◆ CharPoly() [1/3]

◆ CharPoly() [2/3]

◆ CharPoly() [3/3]

◆ MinPoly() [1/2]

◆ MinPoly() [2/2]

◆ MatVecMinPoly()

◆ Rank()

◆ IsSingular()

◆ Det()

◆ Solve()

◆ RandomNullSpaceVector() [1/2]

◆ NullSpaceBasis()

◆ RowRankProfile()

◆ ColumnRankProfile()

◆ RankProfileFromLU()

◆ LeadingSubmatrixRankProfiles()

◆ RowRankProfileSubmatrixIndices()

◆ ColRankProfileSubmatrixIndices()

◆ RowRankProfileSubmatrix()

◆ ColRankProfileSubmatrix()

◆ getTriangular() [1/2]

◆ getTriangular() [2/2]

◆ getEchelonForm() [1/2]

◆ getEchelonForm() [2/2]

◆ getEchelonTransform()

◆ getReducedEchelonForm() [1/2]

◆ getReducedEchelonForm() [2/2]

◆ getReducedEchelonTransform()

◆ LTBruhatGen()

◆ getLTBruhatGen() [1/2]

◆ getLTBruhatGen() [2/2]

◆ LTQSorder()

◆ CompressToBlockBiDiagonal()

◆ ExpandBlockBiDiagonalToBruhat()

◆ Bruhat2EchelonPermutation()

◆ LQUPtoInverseOfFullRankMinor()

◆ RandomNullSpaceVector() [2/2]

◆ productBruhatxTS()

◆ buildMatrix()

◆ fsytrf_UP_RPM()

◆ LUdivine() [2/2]

◆ composePermutationsLLL()

◆ composePermutationsLLM()

◆ composePermutationsMLM()

◆ NonZeroRandomMatrix() [1/2]

◆ NonZeroRandomMatrix() [2/2]

◆ RandomMatrix() [1/2]

◆ RandomMatrix() [2/2]

◆ RandomTriangularMatrix() [1/2]

◆ RandomTriangularMatrix() [2/2]

◆ RandomSymmetricMatrix()

◆ RandomMatrixWithRank() [1/2]

◆ RandomMatrixWithRank() [2/2]

◆ RandomIndexSubset()

◆ RandomPermutation()