GEN03
GEN03 — Generates a stored function table by evaluating a polynomial.
Description
This subroutine generates a stored function table by evaluating a polynomial in x over a fixed interval and with specified coefficients.
Initialization
size -- number of points in the table. Must be a power of 2 or a power-of-2 plus 1.
xval1, xval2 -- left and right values of the x interval over which the polynomial is defined (xval1 < xval2). These will produce the 1st stored value and the (power-of-2 plus l)th stored value respectively in the generated function table.
c0, c1, c2, ..., cn -- coefficients of the nth-order polynomial
C0 + C1x + C2x2 + . . . + Cnxn
Coefficients may be positive or negative real numbers; a zero denotes a missing term in the polynomial. The coefficient list begins in p7, providing a current upper limit of 144 terms.
![[Note]](images/note.png)
|
Note |
|---|---|
|
|
Examples
Here is an example of the GEN03 generator. It uses the file gen03.csd.
Example 1268. Example of the GEN03 generator.
See the sections Real-time Audio and Command Line Flags for more information on using command line flags.
<CsoundSynthesizer> <CsOptions> ; Select audio/midi flags here according to platform -odac ;;;realtime audio out ;-iadc ;;;uncomment -iadc if realtime audio input is needed too ; For Non-realtime ouput leave only the line below: ; -o gen03.wav -W ;;; for file output any platform </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 2 0dbfs = 1 ;example by Russell Pinkston - Univ. of Texas (but slightly modified) gisine ftgen 1, 0, 16384, 10, 1 ;sine wave instr 1 ihertz = cpspch(p4) ipkamp = p5 iwsfn = p6 ;waveshaping function inmfn = p7 ;normalization function aenv linen 1, .01, p3, .1 ;overall amp envelope actrl linen 1, 2, p3, 2 ;waveshaping index control aindex poscil actrl/2, ihertz, gisine ;sine wave to be distorted asignal tablei .5+aindex, iwsfn, 1 ;waveshaping anormal tablei actrl, inmfn,1 ;amplitude normalization asig = asignal*anormal*ipkamp*aenv asig dcblock2 asig ;get rid of possible DC outs asig, asig endin </CsInstruments> <CsScore> ; first four notes are specific Chebyshev polynomials using gen03. The values were obtained from Dodge page 147 f4 0 513 3 -1 1 0 1 ; First-order Chebyshev: x f5 0 257 4 4 1 ; Normalizing function for fn4 f6 0 513 3 -1 1 -1 0 2 ; Second-order Chebyshev: 2x2 - 1 f7 0 257 4 6 1 ; Normalizing function for fn6 f8 0 513 3 -1 1 0 -3 0 4 ; Third-order Chebyshev: 4x3 - 3x f9 0 257 4 8 1 ; Normalizing function for fn8 f10 0 513 3 -1 10 0 -7 0 56 0 -112 0 64 ; Seventh-order Chebyshev: 64x7 - 112x5 + 56x3 - 7x f11 0 257 4 10 1 ; Normalizing function for fn10 f12 0 513 3 -1 1 5 4 3 2 2 1 ; a 4th order polynomial function over the x-interval -1 to 1 f13 0 257 4 12 1 ; Normalizing function for fn12 ; five notes with same fundamental, different waveshape & normalizing functions ; pch amp wsfn nmfn i1 0 3 8.00 .7 4 5 i1 + . . . 6 7 i1 + . . . 8 9 i1 + . . . 10 11 i1 + . . . 12 13 e </CsScore> </CsoundSynthesizer>
These are the diagrams of the waveforms of the GEN03 routines, as used in the example:
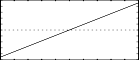
f4 0 513 3 1 1 0 1 - first-order Chebyshev: x
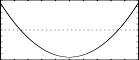
f6 0 513 3 -1 1 -1 0 2 - second-order Chebyshev: 2x2 - 1
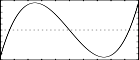
f8 0 513 3 -1 1 0 -3 0 4 - third-order Chebyshev: 4x3 - 3x

f10 0 513 3 -1 10 0 -7 0 56 0 -112 0 64 - seventh-order Chebyshev: 64x7 - 112x5 + 56x3 - 7x
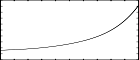
f12 0 513 3 -1 1 5 4 3 2 2 1 - a 4th order polynomial function over the x-interval -1 to 1
See Also
Information about the Chebyshev polynomials on Wikipedia: http://en.wikipedia.org/wiki/Chebyshev_polynomials