Stokes equation model descriptor.
More...
#include <cs_stokes_model.h>
Stokes equation model descriptor.
Members of these Stokes equation model descriptor are publicly accessible, to allow for concise syntax, as it is expected to be used in many places.
◆ arak
Arakawa multiplicator for the Rhie and Chow filter (1 by default).
Please refer to the Rhie and Chow filter section of the theory guide for more informations.
◆ epsdp
parameter of diagonal pressure strengthening
◆ fluid_solid
Has a solid zone where dynamics must be killed?
◆ icalhy
compute the hydrostatic pressure in order to compute the Dirichlet conditions on the pressure at outlets
- 1: calculation of the hydrostatic pressure at the outlet boundary
- 0: no calculation of the hydrostatic pressure at the outlet boundary (default) This option is automatically specified depending on the choice of iphydr and the value of gravity (icalhy = 1 if iphydr = 1 and gravity is different from 0; otherwise icalhy = 0). The activation of this option generates an additional calculation cost (about 30% depending on the case).
If head losses are present just along an outlet boundary, it is necessary to specify icalhy = 0 in order to deactivate the recalculation of the hydrostatic pressure at the boundary, which may otherwise cause instabilities
◆ iccvfg
indicates whether the dynamic field should be frozen or not:
- 1: true
- 0: false (default)
In such a case, the values of velocity, pressure and the variables related to the potential turbulence model ( 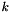 ,
, 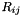 ,
, 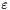 ,
, 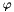 ,
, 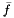 ,
, 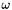 , turbulent viscosity) are kept constant over time and only the equations for the scalars are solved.
, turbulent viscosity) are kept constant over time and only the equations for the scalars are solved.
Also, if iccvfg = 1, the physical properties modified in cs_user_physical_properties will keep being updated. Beware of non-consistencies if these properties would normally affect the dynamic field (modification of density for instance).
Useful if and only if nscal 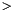 0 and the calculation is a restart.
0 and the calculation is a restart.
◆ idilat
algorithm to take into account the density variation in time
- 0: Boussinesq approximation (rho constant expect in the buoyant term where
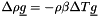
- 1: dilatable steady algorithm (default)
- 2: dilatable unsteady algorithm
- 3: low-Mach algorithm
- 4: algorithm for fire
◆ igprij
improve static pressure algorithm
- 1: take -div(rho R) in the static pressure treatment IF iphydr=1
- 0: no treatment (default)
◆ igpust
improve static pressure algorithm
- 1: take user momentum source terms in the static pressure treatment IF iphydr=1
- 0: no treatment (default)
◆ iifren
indicates the presence of a Bernoulli boundary face (automatically computed)
- 0: no face
- 1: at least one face
◆ iphydr
improve static pressure algorithm Take into account the balance or imbalance between the pressure gradient and source terms (as gravity and head losses)
- 1: impose the equilibrium of the static part of the pressure with any external force, even head losses
- 0: no treatment (default)
- 2: hydrostatic pressure computation with a apriori momentum equation to obtain a hydrostatic pressure taking into account the imbalance between the pressure gradient and the gravity source term.
When the density effects are important, the choice of iphydr = 1 allows to improve the interpolation of the pressure and correct the non-physical velocities which may appear in highly stratified areas or near horizontal walls (thus avoiding the use of extrag if the non-physical velocities are due only to gravity effects).
The improved algorithm also allows eradicating the velocity oscillations which tend to appear at the frontiers of areas with high head losses.
In the case of a stratified flow, the calculation cost is higher when the improved algorithm is used (about 30% depending on the case) because the hydrostatic pressure must be recalculated at the outlet boundary conditions: see icalhy.
On meshes of insufficient quality, in order to improve the convergence, it may be useful to increase the number of iterations for the reconstruction of the pressure right-hand side, i.e. nswrsm.
If head losses are present just along an outlet boundary, it is necessary to specify icalhy = 0 in order to deactivate the recalculation of the hydrostatic pressure at the boundary, which may otherwise cause instabilities. Please refer to the handling of the hydrostatic pressure section of the theory guide for more informations.
◆ iprco
compute the pressure step thanks to the continuity equation
- 1: true (default)
- 0: false
◆ ipucou
indicates the algorithm for velocity/pressure coupling:
- 0: standard algorithm,
- 1: reinforced coupling in case calculation with long time steps
Always useful (it is seldom advised, but it can prove very useful, for instance, in case of flows with weak convection effects and highly variable viscosity).
◆ irecmf
use interpolated face diffusion coefficient instead of cell diffusion coefficient for the mass flux reconstruction for the non-orthogonalities
- 1: true
- 0: false (default)
◆ irevmc
reconstruction of the velocity field with the updated pressure option
- 0: standard gradient of pressure increment (default)
◆ itbrrb
accurate treatment of the wall temperature (reconstruction of wall temperature)
- 1: true
- 0: false (default) (see condli, useful in case of coupling with syrthes)
◆ ivisse
Indicates whether the source terms in transposed gradient and velocity divergence should be taken into account in the momentum equation. In the compressible module, these terms also account for the volume viscosity (cf. viscv0 and iviscv) ![$\partial_i \left[(\kappa -2/3\,(\mu+\mu_t))\partial_k U_k \right] + \partial_j \left[ (\mu+\mu_t)\partial_i U_j \right]$](form_204.png) :
:
- 0: not taken into account,
- 1: taken into account.
The documentation for this struct was generated from the following files:

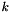 ,
, 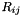 ,
, 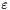 ,
, 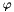 ,
, 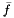 ,
, 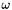 , turbulent viscosity) are kept constant over time and only the equations for the scalars are solved.
, turbulent viscosity) are kept constant over time and only the equations for the scalars are solved. 0 and the calculation is a restart.
0 and the calculation is a restart. 
 1.8.16
1.8.16