|
My Project
programmer's documentation
|
|
My Project
programmer's documentation
|
For Krylov space solvers, default preconditioning is based on a Neumann polynomial of degree poly_degree, with a negative value meaning no preconditioning, and 0 diagonal preconditioning.
For positive values of poly_degree, the preconditioning is explained here: D being the diagonal part of matrix A and X its extra-diagonal part, it can be written 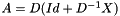 . Therefore
. Therefore 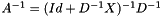 . A series development of
. A series development of 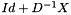 can then be used which yields, symbolically,
can then be used which yields, symbolically,
![\[ Id+\sum\limits_{I=1}^{poly\_degree}\left(-D^{-1}X\right)^{I} \]](form_50.png)
The efficiency of the polynomial preconditioning will vary depending on the system type. In most cases, diagonal or degree 1 provide best results. Each polynomial preconditioning degree above 0 adds one matrix-vector product per inital matrix-vector product of the algorithm. Switching from diagonal to polynomial degree 1 often divides the number of required iterations by approximately 2, but each iteration then costs close to 2 times that of diagonal preconditoning (other vector operations are not doubled), so the net gain is often about 10%. Higher degree polynomials usually lead to diminishing returns.
 1.8.16
1.8.16