My Project: src/base/prehyd.f90 File Reference

My Project

programmer's documentation

Compute an "a priori" hydrostatic pressure and its gradient associated before the Navier Stokes equations (prediction and correction steps navstv.f90). More...

Functions/Subroutines
subroutine	prehyd (grdphd, iterns)

Detailed Description

Compute an "a priori" hydrostatic pressure and its gradient associated before the Navier Stokes equations (prediction and correction steps navstv.f90).

This function computes a hydrostatic pressure 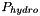$P_{hydro}$ solving an a priori simplified momentum equation:

$\rho^n \dfrac{(\vect{u}^{hydro} - \vect{u}^n)}{\Delta t} = \rho^n \vect{g}^n - \grad P_{hydro}$

and using the mass equation as following:

$\rho^n \divs \left( \delta \vect{u}_{hydro} \right) = 0$

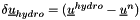
with: $\delta \vect{u}_{hydro} = ( \vect{u}^{hydro} - \vect{u}^n)$

finally, we resolve the simplified momentum equation below:

$\divs \left( K \grad P_{hydro} \right) = \divs \left(\vect{g}\right)$

with the diffusion coefficient ( 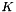$ K $ ) defined as:

$K \equiv \dfrac{1}{\rho^n}$

with a Neumann boundary condition on the hydrostatic pressure:

$D_\fib \left( K, \, P_{hydro} \right) = \vect{g} \cdot \vect{n}_\ib$

(see the theory guide for more details on the boundary condition formulation).

Function/Subroutine Documentation

◆ prehyd()

subroutine prehyd	(	double precision, dimension(ndim, ncelet)	grdphd,
		integer	iterns
	)

Parameters

[out]	grdphd	the a priori hydrostatic pressure gradient 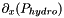$\partial _x (P_{hydro})$
[in]	iterns	Navier-Stokes iteration number