|
My Project
programmer's documentation
|
|
My Project
programmer's documentation
|
C user functions for definition of model options and calculation parameters. These subroutines are called in all cases.
If the Code_Saturne GUI is used, this file is not required (but may be used to override parameters entered through the GUI, and to set parameters not accessible through the GUI).
Several functions are present in the file, each destined to defined specific parameters.
Definition of user variables or properties should be defined here, if not already done throught the GUI.
Most definitions should be done in the cs_user_parameters function (Fortran equivalent is usipsu subroutine).
Choose a turbulent model among the available models
Coupled solver for Rij components (when iturb=30, 31 or 32): 0 to switch off, 1 to switch on
To set a thermal model (0: none, 1: temperature, 2: entyhalpy, 3: total energy)
Volume of Fluid model with mass transfer Merkle model to take into account vaporization / condensation
To activate ALE (Arbitrary Lagrangian Eulerian) method (CS_ALE_NONE: switch off, CS_ALE_LEGACY: legacy solver, CS_ALE_CDO: CDO solver)
The user can add a scalar to be solved
After adding a scalar, the user can add the variance of this scalar
Add a user property defined on a mesh location (cells, interior faces, boundary faces or vertices).
Choose a time step option
Choose a reference time step
To set a duration
For example, to change the log (run_solver.log) verbosity of all the variables:
For example, to change limiters for the convective scheme for a given scalar:
One can also choose the percentage of upwind blending when using the slope test
If one wants to declare a scalar as buoyant (i.e. the density depends on this scalar through a given equation of state) and add it in the velocity-pressure optional sub-iterations (PISO), one can set the dedicated keyword:
If one wants to activate drift terms on a transported scalar:
To set options for the solving of the Stokes problem (velocity pressure coupling see cs_stokes_model_t structure):
To set options for the PISO-like sub iterations (velocity pressure coupling see cs_piso_t structure):
For example, to force the presence of a boundary temperature field, which may be useful for postprocessing:
To add boundary values for all scalars, the following code can be added:
Enforce existence of 'tplus' and 'tstar' fields, so that a Nusselt number may be computed using the post_boundary_nusselt subroutine. When postprocessing this quantity is activated, those fields are present, but if we need to compute them in the cs_user_extra_operations user subroutine without postprocessing them, forcing the definition of these fields to save the values computed for the boundary layer is necessary.
You can activate the post-processing of the Q-criterion on the whole domain mesh with:
Save contribution of slope test for variables in special fields. These fields are automatically created, with postprocessing output enabled, if the matching variable is convected, does not use a pure upwind scheme, and has a slope test (the slope_test_upwind_id key value for a given variable's field is automatically set to the matching postprocessing field's id, or -1 if not applicable).
You can activate the post-processing of clipping on turbulent quantities on the whole domain mesh with:
Frequency of log output.
Change a property's label (here for density, first checking if it is variable). A field's name cannot be changed, but its label, used for logging and postprocessing output, may be redefined.
Activate or deactivate probes output.
Probes for Radiative Transfer (Luminance and radiative density flux vector).
Two modes are available CS_DOMAIN_CDO_MODE_ONLY or CS_DOMAIN_CDO_MODE_WITH_FV
CDO/HHO schemes can be activated within this function as follows:
Several types of domain boundaries can be defined. There are gathered in cs_domain_boundary_type_t The definition of the domain boundaries for CDO/HHO schemes can be specified as follows:
The management of the level and frequency of details written by the code can be specified for CDO/HHO schemes as follows:
The management of the time step with CDO/HHO schemes can be specified as follows:
The computation of the wall distance with CDO schemes is performed as follows:
The add of a user-defined equation solved by CDO/HHO schemes is specified as follows:
The add of a new user-defined property with CDO/HHO schemes is specified as follows:
If you want to compute the Fourier number related to a given property in an unsteady simulation
The definition of an advection field allows one to handle flows with a frozen velocity field or the transport of scalar quantities without solving the Navier-Stokes system. The add of a new user-defined advection field with CDO/HHO schemes is specified as follows:
If you need to activate options related to advection fields, you can also specify
Activation of the groundwater flow module. The second argument is either 0 if no option is needed or a list of flags among CS_GWF_GRAVITATION, CS_GWF_RICHARDS_UNSTEADY, CS_GWF_SOIL_PROPERTY_UNSTEADY, CS_GWF_SOIL_ALL_SATURATED
Add soils (settings of the soil is performed in cs_user_gwf_setup). Soils have to be added before adding tracers.
Add tracer equations which correspond to a transport equation using the darcean flux as the advection field. This call implies the creation of a new equation related to a new variable field name given as arguments. Advanced tracer equations can be defined using cs_gwf_add_tracer_user.
Modifiy the numerical parameters related to a given equation.
When a property has been added, the second step is to define this property. According to the type of property (isotropic, orthotropic or anisotropic) definitions differ. Here are two examples:
When an advection field has been added, the second step is to define this advection field. Here are is an example of definition using an anlytic function and the activation of optional features:
Add terms like diffusion term, advection term, unsteady term, reaction terms or source terms.
By default, Code_Saturne will use a multigrid algorithm for pressure and iterative solver for other variables. For a given case, checking the setup file resulting from a first calculation will provide more info.
Available solvers include a variety of iterative linear solvers, described in more detail at cs_sles_it_create, and a multigrid solver, whose definition and settings are described at cs_multigrid_create, cs_multigrid_set_coarsening_options, and cs_multigrid_set_solver_options.
Simple options may be set using the GUI, but for more advanced settings are described in this section. It is also recommended to read the documentation of cs_sles.c (which is a solver definition "container"), cs_sles_it.c (iterative solvers, with available types cs_sles_it_type_t), and cs_multigrid.c (which are actual solver implementations). The API provided is extensible, so it is possible for a user to define other solvers or link to external solver libraries using this system, without requiring any modification to non-user source files.
The examples which follow illustrate mostly simple setting changes which may be useful.
By default, the wall distance (active only with turbulence models which require it) is computed with a preconditionned conjugate gradient. The following example shows how to use a multigrid solver for this quantity (useful especially if computed repeatedly, such as for ALE).
The following example shows how to set the linear solver for a given user variable field so as to use a BiCGStab solver with polynomial preconditioning of degree 1.
By default, a linear solver uses the same verbosity as its matching variable, and is not verbose for non-variable quantities. The verbosity may be specifically set for linear system resolution, as shown in the following example:
The following example shows how to activate local error visualization output (here for velocity and pressure).
The following example shows how to set advanced settings for the multigrid solver used for the pressure solution.
The following example shows how to use multigrid as a preconditioner for a conjugate gradient solver (for the pressure correction), and set advanced settings for that multigrid preconditioner.
In parallel, grids may optionally be merged across neigboring ranks when their local size becomes too small. This tends to deepen the grid hierarchy, as some parallel rank boundaries are removed. Depending on the architecture and processor/network performance ratios, this may increase or decrease performance.
For DOM radiation models, 1 solver is assigned for each direction this allows using a specific ordering for each direction for the default Block Gauss-Seidel solver.
The example below shows how to set a non-default linear solver for DOM radiation. Here, we assume a quadrature with 32 directions is used (if more solvers than directions are specified, the extra definitions will be unused, but this causes no further issues).
The following example shows how to activate convergence plotting for built-in iterative or multigrid solvers.
Plots will appear as CSV (comma-separated value) files in the monitoring subdirectory.
The following example shows how to setup a solver to use the PETSc library, if the code was built with PETSc support.
General options (those passed to PETSc through command line options) may be defined directly in cs_user_linear_solvers, for example:
A specific system may be set up to use PETsc, as is shown here for the pressure variable:
The basic matrix format to be used by PETSc is defined at this stage, using a PETSc MatType string (see PETSc documentation). Further options may be defined in a setup hook function, as follows:
If no additional settings are required, the matching parameter in cs_sles_petsc_define may be set to NULL.
To use PETSc's GAMG (geometric-algebraic multigrid) preconditioner, the following general options should be set:
Setting GAMG-preconditioned PCG for the pressure may be done as in the previous option, ensuring here that a matrix structure native to PETSc is used (SEQAIJ, MPIAIJ, or some other AIJ variant), so all required matrix operations are available:
With the associated setup hook function:
To use HYPRE's Boomer AMG as a PETSc preconditioner, the following general options should be set:
Setting BoomerAMG-preconditioned PCG for the pressure may be done as in the previous option, ensuring here that a matrix structure native to PETSc is used (SEQAIJ, MPIAIJ, or some other AIJ variant), so all required matrix operations are available:
With the associated setup hook function:
Many additional features are possible with PETSc; for example, the following setup hook also outputs a view of the matrix, depending on an environment variable, CS_USER_PETSC_MAT_VIEW, which may take values DEFAULT, DRAW_WORLD, or DRAW:
Code_Saturne allows the calculation of temporal means or variances, either of expressions evaluated through a user function, or of expressions of the type 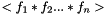 . The variables may be fields or field components. This is done calling either through the GUI, or in the user function cs_user_time_moments. Each temporal mean is declared using either cs_time_moment_define_by_func, or cs_time_moment_define_by_field_ids.
. The variables may be fields or field components. This is done calling either through the GUI, or in the user function cs_user_time_moments. Each temporal mean is declared using either cs_time_moment_define_by_func, or cs_time_moment_define_by_field_ids.
For each time moment, a starting time step or value is defined. If the starting time step number is negative, the time value is used instead.
The moment values are stored as fields, and updated at each time step, using recursive formulas. Before the matching moment computation starting time step, a moment's values are uniformly 0. For visualization an interpretation reasons, only fields of dimension 1, 3, 6, or 9 (scalars, vectors, or tensors of rank 2) are allowed, so moment definitions not matching this constraint should be split.
To count defined moments, use the cs_time_moment_n_moments function, whether from Fortran or C. To access the matching fields, use time_moment_field_id in Fortran, or cs_time_moment_get_field in C.
In the following example, we define a moment for the mean velocity. All components are used (component -1 means all components), so the moment is a vector.
In the next example, we define the variance of the vector velocity. All components are used again (component -1 means all components), so the moment is a tensor.
In the next example, we multiply the expression by the density. As the density is of dimension 1, and the velocity of dimension 3, the resulting moment is of dimension 3.
In the next example, we define a product of several field components, all of dimension 1, as we consider only the x and y components of the velocity; for the density, we cas use either component 0 or -1 (all), since the field is scalar.
This moment's computation is also restarted at each time step.
This next example illustrates the use of user-defined functions to evaluate expressions. Here, we compute the moment of the sum ot two variables (which obviously cannot be expressed as a product), so we first need to define an appropriate function, matching the signature of a cs_time_moment_data_t function. We can name that function as we choose, so naming for clarity is recommmended. Note that in this case, the input argument is not used. This argument may be useful to pass data to the function, or distinguish between calls to a same function.
Note also that we compute both means and variances here.
In cs_user_time_moments, we can now assign that function to a moments definition:
This next example illustrates the use of another user-defined function to evaluate expressions. Here, we compute the moment of the thermal flux at the boundary. We also that we compute both means and variances here.
In cs_user_time_moments, we assign that function to a moments definition:
In this last example, we compute components of the mean velocity in the case of a rotating mesh. As the mesh orientation changes at each time step, it is necessary to compensate for this rotation when computing the mean, relative to a given mesh position. When using the matching moment, it will also be necessary to account for the mesh position.
Here, the same function will be called for each component, so an input array is defined, with a different key (here a simple character) used for each call.
Note that the input arrays must be accessible when updating moments at each time step, so the array of inputs is declared static in cs_user_time_moments. Fo more complex inputs, we would have an array of inputs here; in this simple case, we could pass a simple call id as the input, casting from point to integer.
To activate means for all variables:
Code_Saturne allows modelling of some circular fans as volume regions, defined by simple geometric characteristics, and modeled as explicit momentum source terms in those regions.
Fan pressure characteristic curves are defined as a 2nd order polynomial, and a torque may also be specified. For correct results, it is important that the mesh match the fan dimensions and placement (thickness, hub, blades, and total radius).
The following example shows how a fan may be defined:
 1.8.16
1.8.16