|
My Project
programmer's documentation
|
•All Data Structures Namespaces Files Functions Variables Typedefs Enumerations Enumerator Macros Modules Pages
|
My Project
programmer's documentation
|
Calculation of 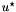 ,
, 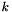 and
and 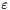 from a diameter
from a diameter 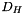 and the reference velocity
and the reference velocity 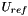 for a circular duct flow with smooth wall (use for inlet boundary conditions).
More...
for a circular duct flow with smooth wall (use for inlet boundary conditions).
More...

Public Member Functions | |
| subroutine | turbulence_bc_ke_hyd_diam (uref2, dh, rho, mu, ustar2, k, eps) |
Calculation of 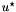 ,
, 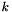 and
and 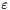 from a diameter
from a diameter 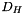 and the reference velocity
and the reference velocity 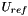 for a circular duct flow with smooth wall (use for inlet boundary conditions).
for a circular duct flow with smooth wall (use for inlet boundary conditions).
Both 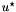 and
and 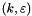 are returned, so that the user may compute other values of
are returned, so that the user may compute other values of 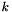 and
and 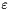 with
with 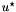 .
.
We use the laws from Idel'Cik, i.e. the head loss coefficient 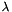 is defined by:
is defined by:
![\[ |\dfrac{\Delta P}{\Delta x}| = \dfrac{\lambda}{D_H} \frac{1}{2} \rho U_{ref}^2 \]](form_102.png)
then the relation reads 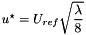 .
. 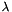 depends on the hydraulic Reynolds number
depends on the hydraulic Reynolds number 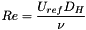 and is given by:
and is given by:
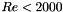
![\[ \lambda = \dfrac{64}{Re} \]](form_107.png)
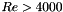
![\[ \lambda = \dfrac{1}{( 1.8 \log_{10}(Re)-1.64 )^2} \]](form_109.png)
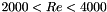 , we complete by a straight line
, we complete by a straight line
![\[ \lambda = 0.021377 + 5.3115. 10^{-6} Re \]](form_111.png)
From 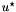 , we can estimate
, we can estimate 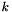 and
and 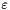 from the well known formulae of developped turbulence
from the well known formulae of developped turbulence
![\[ k = \dfrac{u^{\star 2}}{\sqrt{C_\mu}} \]](form_113.png)
![\[ \varepsilon = \dfrac{ u^{\star 3}}{(\kappa D_H /10)} \]](form_114.png)
| [in] | uref2 | square of the reference flow velocity |
| [in] | dh | hydraulic diameter 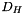 |
| [in] | rho | mass density 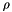 |
| [in] | mu | dynamic viscosity 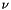 |
| [out] | ustar2 | square of friction speed |
| [out] | k | calculated turbulent intensity 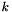 |
| [out] | eps | calculated turbulent dissipation 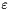 |
| subroutine turbulence_bc_ke_hyd_diam | ( | real(c_double), value | uref2, |
| real(c_double), value | dh, | ||
| real(c_double), value | rho, | ||
| real(c_double), value | mu, | ||
| real(c_double) | ustar2, | ||
| real(c_double) | k, | ||
| real(c_double) | eps | ||
| ) |
 1.8.16
1.8.16