|
My Project
programmer's documentation
|
|
My Project
programmer's documentation
|

Variables | |
| integer, save | ischtp |
| time order of time stepping More... | |
| integer, save | istmpf |
| time order of the mass flux scheme The chosen value for istmpf will automatically determine the value given to the variable thetfl. More... | |
| integer(c_int), pointer, save | nterup |
| number of interations on the pressure-velocity coupling on Navier-Stokes (for the PISO algorithm) More... | |
| integer, save | isno2t |
| isno2t specifies the time scheme activated for the source terms of the momentum equation, apart from convection and diffusion (for instance: head loss, transposed gradient, ...). More... | |
| integer, save | isto2t |
isto2t specifies the time scheme activated for the source terms of the turbulence equations i.e. related to 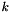 , , 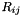 , , 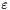 , , 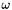 , , 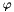 , , 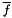 ), apart from convection and diffusion. More... ), apart from convection and diffusion. More... | |
| integer, dimension(nscamx), save | isso2t |
| for each scalar, isso2t specifies the time scheme activated for the source terms of the equation for the scalar, apart from convection and diffusion (for instance: variance production, user-specified terms, ...). More... | |
| integer, save | initvi |
| initvi : =1 if total viscosity read from checkpoint file More... | |
| integer, save | initro |
| initro : =1 if density read from checkpoint file More... | |
| integer, save | initcp |
| initcp : =1 if specific heat read from checkpoint file More... | |
| integer, dimension(nscamx), save | initvs |
| initvs : =1 if scalar diffusivity read from checkpoint file More... | |
| double precision, save | thetsn |
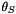 -scheme for the source terms -scheme for the source terms 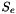 in the Navier-Stokes equations when the source term extrapolation has been activated (see isno2t), following the formula in the Navier-Stokes equations when the source term extrapolation has been activated (see isno2t), following the formula 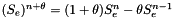 . .The value of 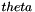 = thetsn is deduced from the value chosen for isno2t. Generally only the value 0.5 is used. More... = thetsn is deduced from the value chosen for isno2t. Generally only the value 0.5 is used. More... | |
| double precision, save | thetst |
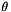 -scheme for the extrapolation of the nonlinear explicit source terms $S_e$ of the turbulence equations when the source term extrapolation has been activated (see isto2t), following the formula -scheme for the extrapolation of the nonlinear explicit source terms $S_e$ of the turbulence equations when the source term extrapolation has been activated (see isto2t), following the formula 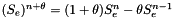 . .The value of 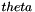 is deduced from the value chosen for isto2t. Generally, only the value 0.5 is used. More... is deduced from the value chosen for isto2t. Generally, only the value 0.5 is used. More... | |
| double precision, dimension(nscamx), save | thetss |
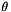 -scheme for the extrapolation of the nonlinear explicit source term -scheme for the extrapolation of the nonlinear explicit source term 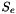 of the scalar transport equation when the source term extrapolation has been activated (see isso2t), following the formula of the scalar transport equation when the source term extrapolation has been activated (see isso2t), following the formula 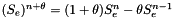 . .The value of 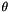 = thetss is deduced from the value chosen for isso2t. Generally, only the value 0.5 is used. More... = thetss is deduced from the value chosen for isso2t. Generally, only the value 0.5 is used. More... | |
| double precision, save | thetfl |
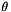 -scheme for the mass flux when a second-order time scheme has been activated for the mass flow (see istmpf). More... -scheme for the mass flux when a second-order time scheme has been activated for the mass flow (see istmpf). More... | |
| double precision, save | thetvi |
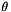 -scheme for the extrapolation of the physical property -scheme for the extrapolation of the physical property 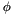 "total viscosity" when the extrapolation has been activated (see time_extrapolated key word), according to the formula "total viscosity" when the extrapolation has been activated (see time_extrapolated key word), according to the formula 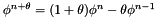 . .The value of 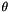 = thetvi is deduced from the value chosen for time_extrapolated key word for the viscosity. Generally, only the value 0.5 is used. More... = thetvi is deduced from the value chosen for time_extrapolated key word for the viscosity. Generally, only the value 0.5 is used. More... | |
| double precision, save | thetcp |
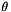 -scheme for the extrapolation of the physical property -scheme for the extrapolation of the physical property 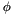 "specific heat" when the extrapolation has been activated (see time_extrapolated field key int), according to the formula "specific heat" when the extrapolation has been activated (see time_extrapolated field key int), according to the formula 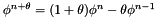 . .The value of 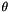 = thetcp is deduced from the value chosen for the specific heat. Generally, only the value 0.5 is used. More... = thetcp is deduced from the value chosen for the specific heat. Generally, only the value 0.5 is used. More... | |
| double precision, dimension(nscamx), save | thetvs |
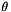 -scheme for the extrapolation of the physical property -scheme for the extrapolation of the physical property 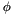 "diffusivity" when the extrapolation has been activated (see time_extrapolated key word), according to the formula "diffusivity" when the extrapolation has been activated (see time_extrapolated key word), according to the formula 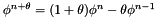 . .The value of 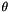 = thetvs is deduced from the value chosen for time_extrapolated key word. Generally, only the value 0.5 is used. More... = thetvs is deduced from the value chosen for time_extrapolated key word. Generally, only the value 0.5 is used. More... | |
| real(c_double), pointer, save | epsup |
| relative precision for the convergence test of the iterative process on pressure-velocity coupling (PISO) More... | |
| real(c_double), pointer, save | xnrmu |
norm of the increment 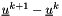 of the iterative process on pressure-velocity coupling (PISO) More... of the iterative process on pressure-velocity coupling (PISO) More... | |
| real(c_double), pointer, save | xnrmu0 |
norm of 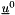 (used by PISO algorithm) More... (used by PISO algorithm) More... | |
| real(c_double), pointer, save epsup |
relative precision for the convergence test of the iterative process on pressure-velocity coupling (PISO)
| integer, save initcp |
initcp : =1 if specific heat read from checkpoint file
| integer, save initro |
initro : =1 if density read from checkpoint file
| integer, save initvi |
initvi : =1 if total viscosity read from checkpoint file
| integer, dimension(nscamx), save initvs |
initvs : =1 if scalar diffusivity read from checkpoint file
| integer, save ischtp |
time order of time stepping
| integer, save isno2t |
isno2t specifies the time scheme activated for the source terms of the momentum equation, apart from convection and diffusion (for instance: head loss, transposed gradient, ...).
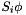 which are linear functions of the solved variable
which are linear functions of the solved variable 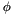 are expressed as second-order terms by interpolation (according to the formula
are expressed as second-order terms by interpolation (according to the formula ![$(S_i\phi)^{n+\theta}=S_i^n[(1-\theta)\phi^n+\theta\phi^{n+1}]$](form_362.png) ,
, 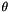 being given by the value of thetav associated with the variable
being given by the value of thetav associated with the variable 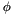 ); the other terms
); the other terms 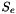 are expressed as second-order terms by extrapolation (according to the formula
are expressed as second-order terms by extrapolation (according to the formula ![$(S_e)^{n+\theta}=[(1+\theta)S_e^n-\theta S_e^{n-1}]$](form_364.png) ,
, 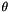 being given by the value of thetsn = 0.5).
being given by the value of thetsn = 0.5).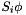 are treated in the same way as when isno2t = 1; the other terms
are treated in the same way as when isno2t = 1; the other terms 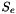 are extrapolated according to the same formula as when isno2t = 1, but with
are extrapolated according to the same formula as when isno2t = 1, but with 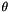 = thetsn = 1. By default, isno2t is initialised to 1 (second-order) when the selected time scheme is second-order (ischtp = 2), otherwise to 0.
= thetsn = 1. By default, isno2t is initialised to 1 (second-order) when the selected time scheme is second-order (ischtp = 2), otherwise to 0. | integer, dimension(nscamx), save isso2t |
for each scalar, isso2t specifies the time scheme activated for the source terms of the equation for the scalar, apart from convection and diffusion (for instance: variance production, user-specified terms, ...).
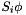 which are linear functions of the solved variable
which are linear functions of the solved variable 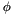 are expressed as second-order terms by interpolation (according to the formula
are expressed as second-order terms by interpolation (according to the formula ![$(S_i\phi)^{n+\theta}=S_i^n[(1-\theta)\phi^n+\theta\phi^{n+1}]$](form_362.png) ,
, 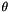 being given by the value of thetav associated with the variable
being given by the value of thetav associated with the variable 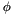 ); the other terms
); the other terms 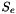 are expressed as second-order terms by extrapolation (according to the formula
are expressed as second-order terms by extrapolation (according to the formula ![$(S_e)^{n+\theta}=[(1+\theta)S_e^n-\theta S_e^{n-1}]$](form_364.png) ,
, 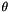 being given by the value of thetss (iscal) = 0.5)
being given by the value of thetss (iscal) = 0.5)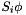 are treated in the same way as when isso2t = 1; the other terms
are treated in the same way as when isso2t = 1; the other terms 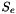 are extrapolated according to the same formula as when isso2t = 1, but with
are extrapolated according to the same formula as when isso2t = 1, but with 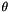 = thetss (iscal) = 1.
= thetss (iscal) = 1.| integer, save istmpf |
time order of the mass flux scheme The chosen value for istmpf will automatically determine the value given to the variable thetfl.
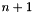 time step.
time step.| integer, save isto2t |
isto2t specifies the time scheme activated for the source terms of the turbulence equations i.e. related to 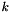 ,
, 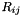 ,
, 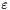 ,
, 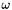 ,
, 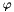 ,
, 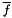 ), apart from convection and diffusion.
), apart from convection and diffusion.
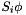 which are linear functions of the solved variable
which are linear functions of the solved variable 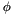 are expressed as second-order terms by interpolation (according to the formula
are expressed as second-order terms by interpolation (according to the formula ![$(S_i\phi)^{n+\theta}=S_i^n[(1-\theta)\phi^n+\theta\phi^{n+1}]$](form_362.png) ,
, 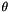 being given by the value of thetav associated with the variable
being given by the value of thetav associated with the variable 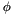 ); the other terms
); the other terms 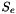 are expressed as second-order terms by extrapolation (according to the formula
are expressed as second-order terms by extrapolation (according to the formula ![$(S_e)^{n+\theta}=[(1+\theta)S_e^n-\theta S_e^{n-1}]$](form_364.png) ,
, 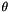 being given by the value of thetst = 0.5)
being given by the value of thetst = 0.5)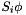 are treated in the same way as when isto2t = 1; the other terms
are treated in the same way as when isto2t = 1; the other terms 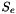 are extrapolated according to the same formula as when isto2t = 1, but with
are extrapolated according to the same formula as when isto2t = 1, but with 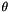 = thetst = 1.
= thetst = 1.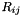 models (iturb = 30 or 31); hence, it is always initialised to 0.
models (iturb = 30 or 31); hence, it is always initialised to 0. | integer(c_int), pointer, save nterup |
number of interations on the pressure-velocity coupling on Navier-Stokes (for the PISO algorithm)
| double precision, save thetcp |
 -scheme for the extrapolation of the physical property
-scheme for the extrapolation of the physical property 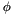 "specific heat" when the extrapolation has been activated (see time_extrapolated field key int), according to the formula
"specific heat" when the extrapolation has been activated (see time_extrapolated field key int), according to the formula 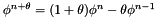 .
.
The value of 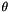 = thetcp is deduced from the value chosen for the specific heat. Generally, only the value 0.5 is used.
= thetcp is deduced from the value chosen for the specific heat. Generally, only the value 0.5 is used.
| double precision, save thetfl |
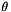 -scheme for the mass flux when a second-order time scheme has been activated for the mass flow (see istmpf).
-scheme for the mass flux when a second-order time scheme has been activated for the mass flow (see istmpf).
| double precision, save thetsn |
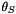 -scheme for the source terms
-scheme for the source terms 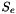 in the Navier-Stokes equations when the source term extrapolation has been activated (see isno2t), following the formula
in the Navier-Stokes equations when the source term extrapolation has been activated (see isno2t), following the formula 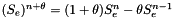 .
.
The value of 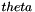 = thetsn is deduced from the value chosen for isno2t. Generally only the value 0.5 is used.
= thetsn is deduced from the value chosen for isno2t. Generally only the value 0.5 is used.
| double precision, dimension(nscamx), save thetss |
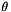 -scheme for the extrapolation of the nonlinear explicit source term
-scheme for the extrapolation of the nonlinear explicit source term 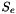 of the scalar transport equation when the source term extrapolation has been activated (see isso2t), following the formula
of the scalar transport equation when the source term extrapolation has been activated (see isso2t), following the formula 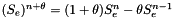 .
.
The value of 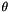 = thetss is deduced from the value chosen for isso2t. Generally, only the value 0.5 is used.
= thetss is deduced from the value chosen for isso2t. Generally, only the value 0.5 is used.
| double precision, save thetst |
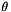 -scheme for the extrapolation of the nonlinear explicit source terms $S_e$ of the turbulence equations when the source term extrapolation has been activated (see isto2t), following the formula
-scheme for the extrapolation of the nonlinear explicit source terms $S_e$ of the turbulence equations when the source term extrapolation has been activated (see isto2t), following the formula 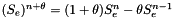 .
.
The value of 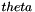 is deduced from the value chosen for isto2t. Generally, only the value 0.5 is used.
is deduced from the value chosen for isto2t. Generally, only the value 0.5 is used.
| double precision, save thetvi |
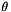 -scheme for the extrapolation of the physical property
-scheme for the extrapolation of the physical property 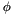 "total viscosity" when the extrapolation has been activated (see time_extrapolated key word), according to the formula
"total viscosity" when the extrapolation has been activated (see time_extrapolated key word), according to the formula 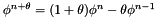 .
.
The value of 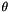 = thetvi is deduced from the value chosen for time_extrapolated key word for the viscosity. Generally, only the value 0.5 is used.
= thetvi is deduced from the value chosen for time_extrapolated key word for the viscosity. Generally, only the value 0.5 is used.
| double precision, dimension(nscamx), save thetvs |
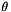 -scheme for the extrapolation of the physical property
-scheme for the extrapolation of the physical property 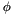 "diffusivity" when the extrapolation has been activated (see time_extrapolated key word), according to the formula
"diffusivity" when the extrapolation has been activated (see time_extrapolated key word), according to the formula 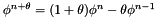 .
.
The value of 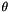 = thetvs is deduced from the value chosen for time_extrapolated key word. Generally, only the value 0.5 is used.
= thetvs is deduced from the value chosen for time_extrapolated key word. Generally, only the value 0.5 is used.
| real(c_double), pointer, save xnrmu |
norm of the increment 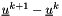 of the iterative process on pressure-velocity coupling (PISO)
of the iterative process on pressure-velocity coupling (PISO)
| real(c_double), pointer, save xnrmu0 |
norm of 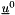 (used by PISO algorithm)
(used by PISO algorithm)
 1.8.16
1.8.16