User subroutine dedicated the use of ALE (Arbitrary Lagrangian Eulerian) Method: More...

Functions/Subroutines
subroutine	usalcl (itrale, nvar, nscal, icodcl, itypfb, ialtyb, impale, dt, rcodcl, xyzno0, disale)

Detailed Description

User subroutine dedicated the use of ALE (Arbitrary Lagrangian Eulerian) Method:

Fills boundary conditions (ialtyb, icodcl, rcodcl) for mesh velocity.
This subroutine also enables one to fix displacement on nodes.

See Examples of data settings for boundary conditions ale (cs_user_boundary_conditions_ale.f90) for examples.

Introduction

Here one defines boundary conditions on a per-face basis.

Boundary faces may be identified using the getfbr subroutine. The syntax of this subroutine is described in cs_user_boundary_conditions.f90 subroutine, but a more thorough description can be found in the user guide.

Boundary conditions setup for standard variables (pressure, velocity, turbulence, scalars) is described precisely in cs_user_boundary_conditions.f90 subroutine.

Detailed explanation will be found in the theory guide.

Boundary condition types

Boundary conditions may be assigned in two ways.

For "standard" boundary conditions

One defines a code in the ialtyb array (of dimensions number of boundary faces). The available codes are:

ialtyb(ifac) = ibfixe: the face ifac is considered to be motionless. A zero Dirichlet boundary condition is automatically imposed on mesh velocity. Moreover the displacement of corresponding nodes will automatically be set to 0 (for further information please read the paragraph dedicated to the description of impale array in the usalcl.f90 subroutine), unless the USER has modified the condition of at least one mesh velocity component (modification of icodcl array, please read the following paragraph For "non-standard" conditions).
ialtyb(ifac) = igliss: The mesh slides on corresponding face ifac. The normal component of mesh velocity is automatically set to 0. A homogeneous Neumann condition is automatically prescribed for the other components, as it's the case for 'Symmetry' fluid condition.
ialtyb(ifac) = ivimpo: the mesh velocity is imposed on face ifac. Thus, the users needs to specify the mesh velocity values filling rcodcl arrays as follows:
- rcodcl(ifac,iuma,1) = mesh velocity in 'x' direction
- rcodcl(ifac,ivma,1) = mesh velocity in 'y' direction
- rcodcl(ifac,iwma,1) = mesh velocity in 'z' direction
Components of rcodcl(.,i.ma,1) arrays that are not specified by user will automatically be set to 0, meaning that user only needs to specify non zero mesh velocity components.

For "non-standard" conditions

Other than (fixed boundary, sliding mesh boundary, fixed velocity), one defines for each face and each component IVAR = IUMA, IVMA, IWMA:

a code
- icodcl(ifac, ivar)
three real values:
- rcodcl(ifac, ivar, 1)
- rcodcl(ifac, ivar, 2)
- rcodcl(ifac, ivar, 3)

The value of icodcl is taken from the following:

1: Dirichlet
3: Neumann
4: Symmetry

The values of the 3 rcodcl components are:

rcodcl(ifac, ivar, 1): Dirichlet for the variable if icodcl(ifac, ivar) = 1 The dimension of rcodcl(ifac, ivar, 1) is in m/s
rcodcl(ifac, ivar, 2): "exterior" exchange coefficient (between the prescribed value and the value at the domain boundary) rinfin = infinite by default rcodcl(ifac,ivar,2) = (VISCMA) / d (D has the dimension of a distance in m, VISCMA stands for the mesh viscosity)
Remarks
the definition of rcodcl(.,.,2) is based on the manner other standard variables are managed in the same case. This type of boundary condition appears nonsense concerning mesh in that context.
rcodcl(ifac,ivar,3) : Flux density (in kg/m s2) = J if icodcl(ifac, ivar) = 3 (<0 if gain, n outwards-facing normal) rcodcl(ifac,ivar,3) = -(VISCMA)* (grad Um).n (Um represents mesh velocity)
Remarks
note that the definition of condition rcodcl(ifac,ivar,3) is based on the manner other standard variables are managed in the same case. rcodcl(.,.,3) = 0.d0 enables one to specify a homogeneous Neuman condition on mesh velocity. Any other value will be physically nonsense in that context.
Note that if the user assigns a value to ialtyb equal to ibfixe, igliss, or ivimpo and does not modify icodcl (zero value by default), ialtyb will define the boundary condition type.

To the contrary, if the user prescribes icodcl(ifac, ivar) (nonzero), the values assigned to rcodcl will be used for the considered face and variable (if rcodcl values are not set, the default values will be used for the face and variable, so:

rcodcl(ifac, ivar, 1) = 0.d0
rcodcl(ifac, ivar, 2) = rinfin
rcodcl(ifac, ivar, 3) = 0.d0)

If the user decides to prescribe his own non-standard boundary conditions it will be necessary to assign values to icodcl AND to rcodcl for ALL mesh velocity components. Thus, the user does not need to assign values to IALTYB for each associated face, as it will not be taken into account in the code.

Consistency rules

A consistency rules between icodcl codes for variables with non-standard boundary conditions:

If a symmetry code (icodcl=4) is imposed for one mesh velocity component, one must have the same condition for all other mesh velocity components.

Fixed displacement on nodes

For a better precision concerning mesh displacement, one can also assign values of displacement to certain internal and/or boundary nodes. Thus, one need to fill DEPALE and impale arrays :

disale(1,inod) = displacement of node inod in 'x' direction
disale(2,inod) = displacement of node inod in 'y' direction
disale(3,inod) = displacement of node inod in 'z' direction This array is defined as the total displacement of the node compared its initial position in initial mesh. impale(inod) = 1 indicates that the displacement of node inod is imposed
Note
Note that impale array is initialized to the value of 0; if its value is not modified, corresponding value in DEPALE array will not be taken into account
During mesh's geometry re-calculation at each time step, the position of the nodes, which displacement is fixed (i.e. impale=1), is not calculated using the value of mesh velocity at the center of corresponding cell, but directly filled using the values of DEPALE.

If the displacement is fixed for all nodes of a boundary face it's not necessary to prescribe boundary conditions at this face on mesh velocity. icodcl and rcodcl values will be overwritten:

icodcl is automatically set to 1 (Dirichlet)
rcodcl value will be automatically set to face's mean mesh velocity value, that is calculated using DEPALE array.

If a fixed boundary condition (ialtyb(ifac)=ibfixe) is imposed to the face ifac, the displacement of each node inod belonging to ifac is considered to be fixed, meaning that impale(inod) = 1 and disale(.,inod) = 0.d0.

Description of nodes

nnod gives the total (internal and boundary) number of nodes. Vertices coordinates are given by xyznod(3, nnod) array. This table is updated at each time step of the calculation. xyzno0(3,nnod) gives the coordinates of initial mesh at the beginning of the calculation.

The faces - nodes connectivity is stored by means of four integer arrays : ipnfac, nodfac, ipnfbr, nodfbr.

nodfac(nodfbr) stores sequentially the index-numbers of the nodes of each internal (boundary) face. ipnfac(ipnfbr) gives the position of the first node of each internal (boundary) face in the array nodfac(nodfbr).

For example, in order to get all nodes of internal face ifac, one can use the following loop:

do ii = ipnfac(ifac), ipnfac(ifac+1)-1 !! index number of nodfac array
                                       !! corresponding to ifac
 
  inod = nodfac(ii)                    !! index-number iith node of face ifac.
  !! ...
enddo

Influence on boundary conditions related to fluid velocity

The effect of fluid velocity and ALE modeling on boundary faces that are declared as walls (itypfb = iparoi or iparug) really depends on the physical nature of this interface.

Indeed when studying an immersed structure the motion of corresponding boundary faces is the one of the structure, meaning that it leads to fluid motion. On the other hand when studying a piston the motion of vertices belonging to lateral boundaries has no physical meaning therefore it has no influence on fluid motion.

Whatever the case, mesh velocity component that is normal to the boundary face is always taken into account ( 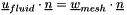$\vect{u}_{fluid} \cdot \vect{n} = \vect{w}_{mesh} \cdot \vect{n}$ ).

The modeling of tangential mesh velocity component differs from one case to another.

The influence of mesh velocity on boundary conditions for fluid modeling is managed and modeled in Code_Saturne as follows:

If ialtyb(ifac) = ibfixe: mesh velocity equals 0. (In case of 'fluid sliding wall' modeling corresponding condition will be specified in Code_Saturne Interface or in cs_user_boundary_conditions.f90 subroutine.)
If ialtyb(ifac) = ivimpo: tangential mesh velocity is modeled as a sliding wall velocity in fluid boundary conditions unless a value for fluid sliding wall velocity has been specified by USER in Code_Saturne Interface or in cs_user_boundary_conditions.f90 subroutine.
If ialtyb(ifac) = igliss: tangential mesh velocity is not taken into account in fluid boundary conditions (In case of 'fluid sliding wall' modeling corresponding condition will be specified in Code_Saturne Interface or in cs_user_boundary_conditions.f90 subroutine.)
If impale(inod) = 1 for all vertices of a boundary face: tangential mesh velocity value that has been derived from nodes displacement is modeled as a sliding wall velocity in fluid boundary conditions unless a value for fluid sliding wall velocity has been specified by USER in Code_Saturne Interface or in 'cs_user_boundary_conditions' subroutine.

Note that mesh velocity has no influence on modeling of boundary faces with 'inlet' or 'free outlet' fluid boundary condition.

For "non standard" conditions USER has to manage the influence of boundary conditions for ALE method (i.e. mesh velocity) on the ones for Navier Stokes equations(i.e. fluid velocity). (Note that fluid boundary conditions can be specified in this subroutine.)

Cells identification

Cells may be identified using the getcel subroutine. The syntax of this subroutine is described in the cs_user_boundary_conditions.f90 subroutine, but a more thorough description can be found in the user guide.

Faces identification

Faces may be identified using the getfbr subroutine. The syntax of this subroutine is described in the cs_user_boundary_conditions.f90 subroutine, but a more thorough description can be found in the user guide.

Function/Subroutine Documentation

◆ usalcl()

subroutine usalcl	(	integer	itrale,
		integer	nvar,
		integer	nscal,
		integer, dimension(nfabor,nvar)	icodcl,
		integer, dimension(nfabor)	itypfb,
		integer, dimension(nfabor)	ialtyb,
		integer, dimension(nnod)	impale,
		double precision, dimension(ncelet)	dt,
		double precision, dimension(nfabor,nvar,3)	rcodcl,
		double precision, dimension(3,nnod)	xyzno0,
		double precision, dimension(3,nnod)	disale
	)

Parameters

[in]	itrale	number of iterations for ALE method
[in]	nvar	total number of variables
[in]	nscal	total number of scalars
[out]	icodcl	boundary condition code: 1 Dirichlet 2 Radiative outlet 3 Neumann 4 sliding and $\vect{u} \cdot \vect{n} = 0$ 5 smooth wall and $\vect{u} \cdot \vect{n} = 0$ 6 rough wall and $\vect{u} \cdot \vect{n} = 0$ 9 free inlet/outlet (input mass flux blocked to 0)
[in,out]	itypfb	boundary face types
[out]	ialtyb	boundary face types for mesh velocity
[in]	impale	indicator for fixed node displacement
[in]	dt	time step (per cell)
[in,out]	rcodcl	boundary condition values: rcodcl(1) value of the dirichlet rcodcl(2) value of the exterior exchange coefficient (infinite if no exchange) rcodcl(3) value flux density (negative if gain) in w/m2 or roughness in m if icodcl=6 for the velocity $(\mu+\mu_T) \gradv \vect{u} \cdot \vect{n}$ for the pressure $\Delta t \grad P \cdot \vect{n}$ for a scalar $cp \left( K + \dfrac{K_T}{\sigma_T} \right) \grad T \cdot \vect{n}$
[in,out]	disale	nodes total displacement (from time 0 to n)
[in]	xyzno0	vertex coordinates of initial mesh

Functions/Subroutines