|
My Project
programmer's documentation
|
|
My Project
programmer's documentation
|
#include <stdlib.h>#include <assert.h>#include <float.h>#include <limits.h>#include <bft_mem.h>#include "cs_blas.h"#include "cs_log.h"#include "cs_math.h"#include "cs_parall.h"#include "cs_sort.h"#include "cs_sdm.h"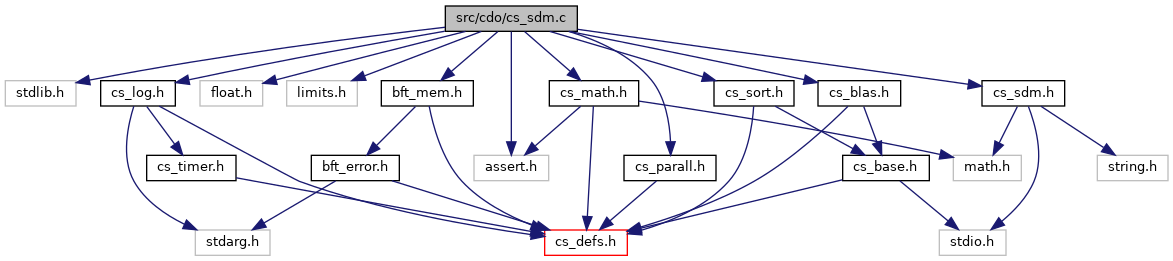
Functions | |
| static cs_sdm_t * | _create_sdm (cs_flag_t flag, int n_max_rows, int n_max_cols) |
| Generic way to allocate a cs_sdm_t structure. More... | |
| cs_sdm_t * | cs_sdm_create (cs_flag_t flag, int n_max_rows, int n_max_cols) |
| Allocate and initialize a cs_sdm_t structure Most generic function to create a cs_sdm_t structure without block description. More... | |
| cs_sdm_t * | cs_sdm_square_create (int n_max_rows) |
| Allocate and initialize a cs_sdm_t structure Case of a square matrix. More... | |
| cs_sdm_t * | cs_sdm_create_copy (const cs_sdm_t *m) |
| Allocate a cs_sdm_t structure and initialized it with the copy of the matrix m in input. More... | |
| cs_sdm_t * | cs_sdm_create_transpose (cs_sdm_t *mat) |
| Define a new matrix which is its transpose. More... | |
| cs_sdm_t * | cs_sdm_block_create (int n_max_blocks_by_row, int n_max_blocks_by_col, const int max_row_block_sizes[], const int max_col_block_sizes[]) |
| Allocate and initialize a cs_sdm_t structure. More... | |
| cs_sdm_t * | cs_sdm_block33_create (int n_max_blocks_by_row, int n_max_blocks_by_col) |
| Allocate and initialize a cs_sdm_t structure by block when the block size is constant and equal to 3. More... | |
| cs_sdm_t * | cs_sdm_free (cs_sdm_t *mat) |
| Free a cs_sdm_t structure. More... | |
| void | cs_sdm_block_init (cs_sdm_t *m, int n_row_blocks, int n_col_blocks, const int row_block_sizes[], const int col_block_sizes[]) |
| Initialize the pattern of cs_sdm_t structure defined by block The matrix should have been allocated before calling this function. More... | |
| void | cs_sdm_block33_init (cs_sdm_t *m, int n_row_blocks, int n_col_blocks) |
| Initialize the pattern of cs_sdm_t structure defined by 3x3 block The matrix should have been allocated before calling this function. More... | |
| cs_sdm_t * | cs_sdm_block_create_copy (const cs_sdm_t *mref) |
| Allocate and initialize a cs_sdm_t structure w.r.t. to a given matrix. More... | |
| void | cs_sdm_multiply (const cs_sdm_t *a, const cs_sdm_t *b, cs_sdm_t *c) |
| Compute a local dense matrix-product c = a*b c has been previously allocated. More... | |
| void | cs_sdm_multiply_rowrow (const cs_sdm_t *a, const cs_sdm_t *b, cs_sdm_t *c) |
| Compute a row-row matrix product of a and b. It is basically equal to the classical a*b^T. It is a fast (matrices are row-major) way of computing a*b if b is symmetric or if b^T is given. Generic version: all compatible sizes. More... | |
| void | cs_sdm_multiply_rowrow_sym (const cs_sdm_t *a, const cs_sdm_t *b, cs_sdm_t *c) |
| Compute a row-row matrix product of a and b. It is basically equal to the classical a*b^T. It is a fast (matrices are row-major) way of computing a*b if b is symmetric or if b^T is given. Generic version: all compatible sizes Result is known to be symmetric. More... | |
| void | cs_sdm_block_multiply_rowrow (const cs_sdm_t *a, const cs_sdm_t *b, cs_sdm_t *c) |
| Compute a row-row matrix product of a and b. It is basically equal to the classical a*b^T. It is a fast (matrices are row-major) way of computing a*b if b is symmetric or if b^T is given. Case of matrices defined by block. More... | |
| void | cs_sdm_block_multiply_rowrow_sym (const cs_sdm_t *a, const cs_sdm_t *b, cs_sdm_t *c) |
| Compute a row-row matrix product of a and b. It is basically equal to the classical a*b^T. It is a fast (matrices are row-major) way of computing a*b if b is symmetric or if b^T is given. Case of matrices defined by block. Results is known to be symmetric. More... | |
| void | cs_sdm_square_matvec (const cs_sdm_t *mat, const cs_real_t *vec, cs_real_t *mv) |
| Compute a dense matrix-vector product for a small square matrix mv has been previously allocated. More... | |
| void | cs_sdm_matvec (const cs_sdm_t *mat, const cs_real_t *vec, cs_real_t *mv) |
| Compute a dense matrix-vector product for a rectangular matrix mv has been previously allocated. More... | |
| void | cs_sdm_update_matvec (const cs_sdm_t *mat, const cs_real_t *vec, cs_real_t *mv) |
| Compute a dense matrix-vector product for a rectangular matrix mv has been previously allocated and initialized Thus mv is updated inside this function. More... | |
| void | cs_sdm_matvec_transposed (const cs_sdm_t *mat, const cs_real_t *vec, cs_real_t *mv) |
| Compute a dense matrix-vector product for a rectangular matrix which is transposed. mv has been previously allocated. mv is updated inside this function. Don't forget to initialize mv if needed. More... | |
| void | cs_sdm_block_add (cs_sdm_t *mat, const cs_sdm_t *add) |
| Add two matrices defined by block: loc += add. More... | |
| void | cs_sdm_block_add_mult (cs_sdm_t *mat, cs_real_t mult_coef, const cs_sdm_t *add) |
| Add two matrices defined by block: loc += mult_coef * add. More... | |
| void | cs_sdm_block_matvec (const cs_sdm_t *mat, const cs_real_t *vec, cs_real_t *mv) |
| Compute a dense matrix-vector product for a rectangular matrix defined by block mv has been previously allocated. More... | |
| void | cs_sdm_add (cs_sdm_t *mat, const cs_sdm_t *add) |
| Add two small dense matrices: loc += add. More... | |
| void | cs_sdm_add_mult (cs_sdm_t *mat, cs_real_t alpha, const cs_sdm_t *add) |
| Add two small dense matrices: loc += alpha*add. More... | |
| void | cs_sdm_square_add_transpose (cs_sdm_t *mat, cs_sdm_t *tr) |
| Define a new matrix by adding the given matrix with its transpose. Keep the transposed matrix for a future use. More... | |
| void | cs_sdm_square_2symm (cs_sdm_t *mat) |
| Set the given matrix to two times its symmetric part mat --> mat + mat_tr = 2*symm(mat) More... | |
| void | cs_sdm_square_asymm (cs_sdm_t *mat) |
| Set the given matrix into its anti-symmetric part. More... | |
| void | cs_sdm_block_square_asymm (cs_sdm_t *mat) |
| Set the given block matrix into its anti-symmetric part. More... | |
| void | cs_sdm_33_sym_qr_compute (const cs_real_t m[9], cs_real_t Qt[9], cs_real_t R[6]) |
| Decompose a matrix into the matrix product Q.R Case of a 3x3 symmetric matrix. More... | |
| void | cs_sdm_33_lu_compute (const cs_sdm_t *m, cs_real_t facto[9]) |
| LU factorization of a small dense 3x3 matrix. More... | |
| void | cs_sdm_lu_compute (const cs_sdm_t *m, cs_real_t facto[]) |
| LU factorization of a small dense matrix. Small means that the number m->n_rows is less than 100 for instance. More... | |
| void | cs_sdm_33_lu_solve (const cs_real_t facto[9], const cs_real_t rhs[3], cs_real_t sol[3]) |
| Solve a system A.sol = rhs using a LU factorization of A (a small 3x3 dense matrix). More... | |
| void | cs_sdm_lu_solve (cs_lnum_t n_rows, const cs_real_t facto[], const cs_real_t *rhs, cs_real_t *sol) |
| Solve a system A.sol = rhs using a LU factorization of A (a small dense matrix). More... | |
| void | cs_sdm_33_ldlt_compute (const cs_sdm_t *m, cs_real_t facto[6]) |
| LDL^T: Modified Cholesky decomposition of a 3x3 SPD matrix. For more reference, see for instance http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf. More... | |
| void | cs_sdm_44_ldlt_compute (const cs_sdm_t *m, cs_real_t facto[10]) |
| LDL^T: Modified Cholesky decomposition of a 4x4 SPD matrix. For more reference, see for instance http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf. More... | |
| void | cs_sdm_66_ldlt_compute (const cs_sdm_t *m, cs_real_t facto[21]) |
| LDL^T: Modified Cholesky decomposition of a 6x6 SPD matrix. For more reference, see for instance http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf. More... | |
| void | cs_sdm_ldlt_compute (const cs_sdm_t *m, cs_real_t *facto, cs_real_t *dkk) |
| LDL^T: Modified Cholesky decomposition of a SPD matrix. For more reference, see for instance http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf. More... | |
| void | cs_sdm_33_ldlt_solve (const cs_real_t facto[6], const cs_real_t rhs[3], cs_real_t sol[3]) |
| Solve a 3x3 matrix with a modified Cholesky decomposition (L.D.L^T) The solution should be already allocated Ref. http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf. More... | |
| void | cs_sdm_44_ldlt_solve (const cs_real_t facto[10], const cs_real_t rhs[4], cs_real_t x[4]) |
| Solve a 4x4 matrix with a modified Cholesky decomposition (L.D.L^T) The solution should be already allocated Ref. http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf. More... | |
| void | cs_sdm_66_ldlt_solve (const cs_real_t f[21], const cs_real_t b[6], cs_real_t x[6]) |
| Solve a 6x6 matrix with a modified Cholesky decomposition (L.D.L^T) The solution should be already allocated Ref. http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf. More... | |
| void | cs_sdm_ldlt_solve (int n_rows, const cs_real_t *facto, const cs_real_t *rhs, cs_real_t *sol) |
| Solve a SPD matrix with a L.D.L^T (Modified Cholesky decomposition) The solution should be already allocated Reference: http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf. More... | |
| double | cs_sdm_test_symmetry (const cs_sdm_t *mat) |
| Test if a matrix is symmetric. Return 0. if the extradiagonal differences are lower thann the machine precision. More... | |
| void | cs_sdm_simple_dump (const cs_sdm_t *mat) |
| Dump a small dense matrix. More... | |
| void | cs_sdm_dump (cs_lnum_t parent_id, const cs_lnum_t *row_ids, const cs_lnum_t *col_ids, const cs_sdm_t *mat) |
| Dump a small dense matrix. More... | |
| void | cs_sdm_fprintf (FILE *fp, const char *fname, cs_real_t thd, const cs_sdm_t *m) |
| Print a cs_sdm_t structure not defined by block Print into the file f if given otherwise open a new file named fname if given otherwise print into the standard output The usage of threshold allows one to compare more easier matrices without taking into account numerical roundoff. More... | |
| void | cs_sdm_block_dump (cs_lnum_t parent_id, const cs_sdm_t *mat) |
| Dump a small dense matrix defined by blocks. More... | |
| void | cs_sdm_block_fprintf (FILE *fp, const char *fname, cs_real_t thd, const cs_sdm_t *m) |
| Print a cs_sdm_t structure which is defined by block Print into the file f if given otherwise open a new file named fname if given otherwise print into the standard output The usage of threshold allows one to compare more easier matrices without taking into account numerical roundoff. More... | |
Variables | |
| static const char | _msg_small_p [] |
|
static |
Generic way to allocate a cs_sdm_t structure.
| [in] | flag | metadata related to a cs_sdm_t structure |
| [in] | n_max_rows | max number of rows |
| [in] | n_max_cols | max number of columns |
| [in] | n_max_rows | max number of rows |
| [in] | n_max_cols | max number of columns |
| void cs_sdm_33_ldlt_compute | ( | const cs_sdm_t * | m, |
| cs_real_t | facto[6] | ||
| ) |
LDL^T: Modified Cholesky decomposition of a 3x3 SPD matrix. For more reference, see for instance http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf.
| [in] | m | pointer to a cs_sdm_t structure |
| [in,out] | facto | vector of the coefficient of the decomposition |
Solve a 3x3 matrix with a modified Cholesky decomposition (L.D.L^T) The solution should be already allocated Ref. http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf.
| [in] | facto | vector of the coefficients of the decomposition |
| [in] | rhs | right-hand side |
| [in,out] | sol | solution |
| void cs_sdm_33_lu_compute | ( | const cs_sdm_t * | m, |
| cs_real_t | facto[9] | ||
| ) |
LU factorization of a small dense 3x3 matrix.
| [in] | m | pointer to a cs_sdm_t structure |
| [in,out] | facto | compact storage of coefficients for the LU factorization |
Solve a system A.sol = rhs using a LU factorization of A (a small 3x3 dense matrix).
| [in] | facto | compact storage of coefficients for the LU factorization (should be allocated to the right size, i.e. n_rows*n_rows) |
| [in] | rhs | right-hand side |
| [in,out] | sol | solution |
Decompose a matrix into the matrix product Q.R Case of a 3x3 symmetric matrix.
| [in] | m | matrix values |
| [in,out] | Qt | transposed of matrix Q |
| [in,out] | R | vector of the coefficient of the decomposition |
j= 0, 1, 2 i=0| 0| 1| 2| i=1 | 4| 5| i=2 6|
| void cs_sdm_44_ldlt_compute | ( | const cs_sdm_t * | m, |
| cs_real_t | facto[10] | ||
| ) |
LDL^T: Modified Cholesky decomposition of a 4x4 SPD matrix. For more reference, see for instance http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf.
| [in] | m | pointer to a cs_sdm_t structure |
| [in,out] | facto | vector of the coefficient of the decomposition |
Solve a 4x4 matrix with a modified Cholesky decomposition (L.D.L^T) The solution should be already allocated Ref. http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf.
| [in] | facto | vector of the coefficients of the decomposition |
| [in] | rhs | right-hand side |
| [in,out] | x | solution |
| void cs_sdm_66_ldlt_compute | ( | const cs_sdm_t * | m, |
| cs_real_t | facto[21] | ||
| ) |
LDL^T: Modified Cholesky decomposition of a 6x6 SPD matrix. For more reference, see for instance http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf.
| [in] | m | pointer to a cs_sdm_t structure |
| [in,out] | facto | vector of the coefficient of the decomposition |
Solve a 6x6 matrix with a modified Cholesky decomposition (L.D.L^T) The solution should be already allocated Ref. http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf.
| [in] | f | vector of the coefficients of the decomposition |
| [in] | b | right-hand side |
| [in,out] | x | solution |
| void cs_sdm_add | ( | cs_sdm_t * | mat, |
| const cs_sdm_t * | add | ||
| ) |
Add two small dense matrices: loc += add.
| [in,out] | mat | local matrix storing the result |
| [in] | add | values to add to mat |
| void cs_sdm_add_mult | ( | cs_sdm_t * | mat, |
| cs_real_t | alpha, | ||
| const cs_sdm_t * | add | ||
| ) |
Add two small dense matrices: loc += alpha*add.
| [in,out] | mat | local matrix storing the result |
| [in] | alpha | multiplicative coefficient |
| [in] | add | values to add to mat |
| cs_sdm_t* cs_sdm_block33_create | ( | int | n_max_blocks_by_row, |
| int | n_max_blocks_by_col | ||
| ) |
Allocate and initialize a cs_sdm_t structure by block when the block size is constant and equal to 3.
| [in] | n_max_blocks_by_row | max number of blocks in a row |
| [in] | n_max_blocks_by_col | max number of blocks in a column |
| void cs_sdm_block33_init | ( | cs_sdm_t * | m, |
| int | n_row_blocks, | ||
| int | n_col_blocks | ||
| ) |
Initialize the pattern of cs_sdm_t structure defined by 3x3 block The matrix should have been allocated before calling this function.
| [in,out] | m | |
| [in] | n_row_blocks | number of blocks in a row |
| [in] | n_col_blocks | number of blocks in a column |
| void cs_sdm_block_add | ( | cs_sdm_t * | mat, |
| const cs_sdm_t * | add | ||
| ) |
Add two matrices defined by block: loc += add.
| [in,out] | mat | local matrix storing the result |
| [in] | add | values to add to mat |
| void cs_sdm_block_add_mult | ( | cs_sdm_t * | mat, |
| cs_real_t | mult_coef, | ||
| const cs_sdm_t * | add | ||
| ) |
Add two matrices defined by block: loc += mult_coef * add.
| [in,out] | mat | local matrix storing the result |
| [in] | mult_coef | multiplicative coefficient |
| [in] | add | values to add to mat |
| cs_sdm_t* cs_sdm_block_create | ( | int | n_max_blocks_by_row, |
| int | n_max_blocks_by_col, | ||
| const int | max_row_block_sizes[], | ||
| const int | max_col_block_sizes[] | ||
| ) |
Allocate and initialize a cs_sdm_t structure.
| [in] | n_max_blocks_by_row | max number of blocks in a row |
| [in] | n_max_blocks_by_col | max number of blocks in a column |
| [in] | max_row_block_sizes | max number of rows by block in a column |
| [in] | max_col_block_sizes | max number of columns by block in a row |
| cs_sdm_t* cs_sdm_block_create_copy | ( | const cs_sdm_t * | mref | ) |
Allocate and initialize a cs_sdm_t structure w.r.t. to a given matrix.
| [in] | mref | pointer to a matrix to copy |
| void cs_sdm_block_dump | ( | cs_lnum_t | parent_id, |
| const cs_sdm_t * | mat | ||
| ) |
Dump a small dense matrix defined by blocks.
| [in] | parent_id | id of the related parent entity |
| [in] | mat | pointer to the cs_sdm_t structure |
| void cs_sdm_block_fprintf | ( | FILE * | fp, |
| const char * | fname, | ||
| cs_real_t | thd, | ||
| const cs_sdm_t * | m | ||
| ) |
Print a cs_sdm_t structure which is defined by block Print into the file f if given otherwise open a new file named fname if given otherwise print into the standard output The usage of threshold allows one to compare more easier matrices without taking into account numerical roundoff.
| [in] | fp | pointer to a file structure or NULL |
| [in] | fname | filename or NULL |
| [in] | thd | threshold (below this value --> set 0) |
| [in] | m | pointer to the cs_sdm_t structure |
| void cs_sdm_block_init | ( | cs_sdm_t * | m, |
| int | n_row_blocks, | ||
| int | n_col_blocks, | ||
| const int | row_block_sizes[], | ||
| const int | col_block_sizes[] | ||
| ) |
Initialize the pattern of cs_sdm_t structure defined by block The matrix should have been allocated before calling this function.
| [in,out] | m | |
| [in] | n_row_blocks | number of blocks in a row |
| [in] | n_col_blocks | number of blocks in a column |
| [in] | row_block_sizes | number of rows by block in a column |
| [in] | col_block_sizes | number of columns by block in a row |
Compute a dense matrix-vector product for a rectangular matrix defined by block mv has been previously allocated.
| [in] | mat | local matrix to use |
| [in] | vec | local vector to use (size = mat->n_cols) |
| [in,out] | mv | result of the operation (size = mat->n_rows) |
| void cs_sdm_block_multiply_rowrow | ( | const cs_sdm_t * | a, |
| const cs_sdm_t * | b, | ||
| cs_sdm_t * | c | ||
| ) |
Compute a row-row matrix product of a and b. It is basically equal to the classical a*b^T. It is a fast (matrices are row-major) way of computing a*b if b is symmetric or if b^T is given. Case of matrices defined by block.
Compute a row-row matrix product of a and b. It is basically equal to the classical a*b^T. It is a fast (matrices are row-major) way of computing a*b if b is symmetric or if b^T is given. Case of a matrix defined by block.
| [in] | a | local matrix to use |
| [in] | b | local matrix to use |
| [in,out] | c | result of the local matrix-product (already allocated) is updated |
| void cs_sdm_block_multiply_rowrow_sym | ( | const cs_sdm_t * | a, |
| const cs_sdm_t * | b, | ||
| cs_sdm_t * | c | ||
| ) |
Compute a row-row matrix product of a and b. It is basically equal to the classical a*b^T. It is a fast (matrices are row-major) way of computing a*b if b is symmetric or if b^T is given. Case of matrices defined by block. Results is known to be symmetric.
| [in] | a | local matrix to use |
| [in] | b | local matrix to use |
| [in,out] | c | result of the local matrix-product (already allocated) is updated |
| void cs_sdm_block_square_asymm | ( | cs_sdm_t * | mat | ) |
Set the given block matrix into its anti-symmetric part.
| [in,out] | mat | small dense matrix defined by block to transform |
| cs_sdm_t* cs_sdm_create | ( | cs_flag_t | flag, |
| int | n_max_rows, | ||
| int | n_max_cols | ||
| ) |
Allocate and initialize a cs_sdm_t structure Most generic function to create a cs_sdm_t structure without block description.
Allocate and initialize a cs_sdm_t structure Most generic function to create a cs_sdm_t structure.
| [in] | flag | metadata related to a cs_sdm_t structure |
| [in] | n_max_rows | max number of rows |
| [in] | n_max_cols | max number of columns |
| cs_sdm_t* cs_sdm_create_copy | ( | const cs_sdm_t * | m | ) |
Allocate a cs_sdm_t structure and initialized it with the copy of the matrix m in input.
| [in] | m | pointer to a cs_sdm_t structure to copy |
| cs_sdm_t* cs_sdm_create_transpose | ( | cs_sdm_t * | mat | ) |
Define a new matrix which is its transpose.
| [in] | mat | local matrix to transpose |
| void cs_sdm_dump | ( | cs_lnum_t | parent_id, |
| const cs_lnum_t * | row_ids, | ||
| const cs_lnum_t * | col_ids, | ||
| const cs_sdm_t * | mat | ||
| ) |
Dump a small dense matrix.
| [in] | parent_id | id of the related parent entity |
| [in] | row_ids | list of ids related to associated entities (or NULL) |
| [in] | col_ids | list of ids related to associated entities (or NULL) |
| [in] | mat | pointer to the cs_sdm_t structure |
| void cs_sdm_fprintf | ( | FILE * | fp, |
| const char * | fname, | ||
| cs_real_t | thd, | ||
| const cs_sdm_t * | m | ||
| ) |
Print a cs_sdm_t structure not defined by block Print into the file f if given otherwise open a new file named fname if given otherwise print into the standard output The usage of threshold allows one to compare more easier matrices without taking into account numerical roundoff.
| [in] | fp | pointer to a file structure or NULL |
| [in] | fname | filename or NULL |
| [in] | thd | threshold (below this value --> set 0) |
| [in] | m | pointer to the cs_sdm_t structure |
| cs_sdm_t* cs_sdm_free | ( | cs_sdm_t * | mat | ) |
Free a cs_sdm_t structure.
| [in] | mat | pointer to a cs_sdm_t struct. to free |
LDL^T: Modified Cholesky decomposition of a SPD matrix. For more reference, see for instance http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf.
| [in] | m | pointer to a cs_sdm_t structure |
| [in,out] | facto | vector of the coefficient of the decomposition |
| [in,out] | dkk | store temporary the diagonal (size = n_rows) |
| void cs_sdm_ldlt_solve | ( | int | n_rows, |
| const cs_real_t * | facto, | ||
| const cs_real_t * | rhs, | ||
| cs_real_t * | sol | ||
| ) |
Solve a SPD matrix with a L.D.L^T (Modified Cholesky decomposition) The solution should be already allocated Reference: http://mathforcollege.com/nm/mws/gen/04sle/mws_gen_sle_txt_cholesky.pdf.
| [in] | n_rows | dimension of the system to solve |
| [in] | facto | vector of the coefficients of the decomposition |
| [in] | rhs | right-hand side |
| [in,out] | sol | solution |
| void cs_sdm_lu_compute | ( | const cs_sdm_t * | m, |
| cs_real_t | facto[] | ||
| ) |
LU factorization of a small dense matrix. Small means that the number m->n_rows is less than 100 for instance.
| [in] | m | pointer to a cs_sdm_t structure |
| [in,out] | facto | compact storage of coefficients for the LU factorization (should be allocated to the right size, i.e. m->n_rows*m->n_rows) |
| void cs_sdm_lu_solve | ( | cs_lnum_t | n_rows, |
| const cs_real_t | facto[], | ||
| const cs_real_t * | rhs, | ||
| cs_real_t * | sol | ||
| ) |
Solve a system A.sol = rhs using a LU factorization of A (a small dense matrix).
| [in] | n_rows | dimension of the system to solve |
| [in] | facto | compact storage of coefficients for the LU factorization (should be allocated to the right size, i.e. n_rows*n_rows) |
| [in] | rhs | right-hand side |
| [in,out] | sol | solution |
Compute a dense matrix-vector product for a rectangular matrix mv has been previously allocated.
| [in] | mat | local matrix to use |
| [in] | vec | local vector to use (size = mat->n_cols) |
| [in,out] | mv | result of the operation (size = mat->n_rows) |
Compute a dense matrix-vector product for a rectangular matrix which is transposed. mv has been previously allocated. mv is updated inside this function. Don't forget to initialize mv if needed.
| [in] | mat | local matrix to use |
| [in] | vec | local vector to use (size = mat->n_cols) |
| [in,out] | mv | result of the operation (size = mat->n_rows) |
| void cs_sdm_multiply | ( | const cs_sdm_t * | a, |
| const cs_sdm_t * | b, | ||
| cs_sdm_t * | c | ||
| ) |
Compute a local dense matrix-product c = a*b c has been previously allocated.
| [in] | a | local dense matrix to use |
| [in] | b | local dense matrix to use |
| [in,out] | c | result of the local matrix-product is updated |
| void cs_sdm_multiply_rowrow | ( | const cs_sdm_t * | a, |
| const cs_sdm_t * | b, | ||
| cs_sdm_t * | c | ||
| ) |
Compute a row-row matrix product of a and b. It is basically equal to the classical a*b^T. It is a fast (matrices are row-major) way of computing a*b if b is symmetric or if b^T is given. Generic version: all compatible sizes.
| [in] | a | local matrix to use |
| [in] | b | local matrix to use |
| [in,out] | c | result of the local matrix-product (already allocated) is updated. |
| void cs_sdm_multiply_rowrow_sym | ( | const cs_sdm_t * | a, |
| const cs_sdm_t * | b, | ||
| cs_sdm_t * | c | ||
| ) |
Compute a row-row matrix product of a and b. It is basically equal to the classical a*b^T. It is a fast (matrices are row-major) way of computing a*b if b is symmetric or if b^T is given. Generic version: all compatible sizes Result is known to be symmetric.
| [in] | a | local matrix to use |
| [in] | b | local matrix to use |
| [in,out] | c | result of the local matrix-product (already allocated) is updated. |
| void cs_sdm_simple_dump | ( | const cs_sdm_t * | mat | ) |
Dump a small dense matrix.
| [in] | mat | pointer to the cs_sdm_t structure |
| void cs_sdm_square_2symm | ( | cs_sdm_t * | mat | ) |
Set the given matrix to two times its symmetric part mat --> mat + mat_tr = 2*symm(mat)
| [in,out] | mat | small dense matrix to transform |
| void cs_sdm_square_add_transpose | ( | cs_sdm_t * | mat, |
| cs_sdm_t * | tr | ||
| ) |
Define a new matrix by adding the given matrix with its transpose. Keep the transposed matrix for a future use.
| [in,out] | mat | local matrix to transpose and add |
| [in,out] | tr | transposed of the local matrix |
| void cs_sdm_square_asymm | ( | cs_sdm_t * | mat | ) |
Set the given matrix into its anti-symmetric part.
| [in,out] | mat | small dense matrix to transform |
| cs_sdm_t* cs_sdm_square_create | ( | int | n_max_rows | ) |
Allocate and initialize a cs_sdm_t structure Case of a square matrix.
| [in] | n_max_rows | max number of rows |
Compute a dense matrix-vector product for a small square matrix mv has been previously allocated.
| [in] | mat | local matrix to use |
| [in] | vec | local vector to use |
| [in,out] | mv | result of the local matrix-vector product |
| double cs_sdm_test_symmetry | ( | const cs_sdm_t * | mat | ) |
Test if a matrix is symmetric. Return 0. if the extradiagonal differences are lower thann the machine precision.
| [in] | mat | pointer to the cs_sdm_t structure to test |
Compute a dense matrix-vector product for a rectangular matrix mv has been previously allocated and initialized Thus mv is updated inside this function.
| [in] | mat | local matrix to use |
| [in] | vec | local vector to use (size = mat->n_cols) |
| [in,out] | mv | result of the operation (size = mat->n_rows) |
|
static |
 1.8.16
1.8.16