|
My Project
programmer's documentation
|
|
My Project
programmer's documentation
|
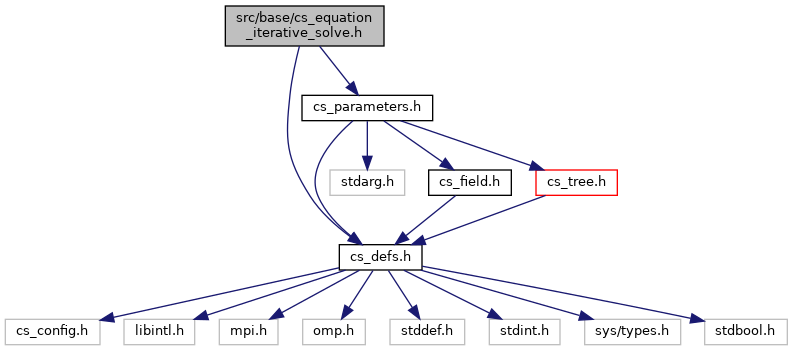
Go to the source code of this file.
Functions | |
| void | cs_equation_iterative_solve_scalar (int idtvar, int iterns, int f_id, const char *name, int iescap, int imucpp, cs_real_t normp, cs_var_cal_opt_t *var_cal_opt, const cs_real_t pvara[], const cs_real_t pvark[], const cs_real_t coefap[], const cs_real_t coefbp[], const cs_real_t cofafp[], const cs_real_t cofbfp[], const cs_real_t i_massflux[], const cs_real_t b_massflux[], const cs_real_t i_viscm[], const cs_real_t b_viscm[], const cs_real_t i_visc[], const cs_real_t b_visc[], cs_real_6_t viscel[], const cs_real_2_t weighf[], const cs_real_t weighb[], int icvflb, const int icvfli[], const cs_real_t rovsdt[], cs_real_t smbrp[], cs_real_t pvar[], cs_real_t dpvar[], const cs_real_t xcpp[], cs_real_t eswork[]) |
This function solves an advection diffusion equation with source terms for one time step for the variable 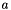 . More... . More... | |
| void | cs_equation_iterative_solve_vector (int idtvar, int iterns, int f_id, const char *name, int ivisep, int iescap, cs_var_cal_opt_t *var_cal_opt, const cs_real_3_t pvara[], const cs_real_3_t pvark[], const cs_real_3_t coefav[], const cs_real_33_t coefbv[], const cs_real_3_t cofafv[], const cs_real_33_t cofbfv[], const cs_real_t i_massflux[], const cs_real_t b_massflux[], cs_real_t i_viscm[], const cs_real_t b_viscm[], const cs_real_t i_visc[], const cs_real_t b_visc[], const cs_real_t secvif[], const cs_real_t secvib[], cs_real_6_t viscel[], const cs_real_2_t weighf[], const cs_real_t weighb[], int icvflb, const int icvfli[], const cs_real_33_t fimp[], cs_real_3_t smbrp[], cs_real_3_t pvar[], cs_real_3_t eswork[]) |
This function solves an advection diffusion equation with source terms for one time step for the vector variable 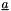 . More... . More... | |
| void | cs_equation_iterative_solve_tensor (int idtvar, int f_id, const char *name, cs_var_cal_opt_t *var_cal_opt, const cs_real_6_t pvara[], const cs_real_6_t pvark[], const cs_real_6_t coefats[], const cs_real_66_t coefbts[], const cs_real_6_t cofafts[], const cs_real_66_t cofbfts[], const cs_real_t i_massflux[], const cs_real_t b_massflux[], const cs_real_t i_viscm[], const cs_real_t b_viscm[], const cs_real_t i_visc[], const cs_real_t b_visc[], cs_real_6_t viscel[], const cs_real_2_t weighf[], const cs_real_t weighb[], int icvflb, const int icvfli[], const cs_real_66_t fimp[], cs_real_6_t smbrp[], cs_real_6_t pvar[]) |
This function solves an advection diffusion equation with source terms for one time step for the symmetric tensor variable 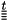 . More... . More... | |
| void cs_equation_iterative_solve_scalar | ( | int | idtvar, |
| int | iterns, | ||
| int | f_id, | ||
| const char * | name, | ||
| int | iescap, | ||
| int | imucpp, | ||
| cs_real_t | normp, | ||
| cs_var_cal_opt_t * | var_cal_opt, | ||
| const cs_real_t | pvara[], | ||
| const cs_real_t | pvark[], | ||
| const cs_real_t | coefap[], | ||
| const cs_real_t | coefbp[], | ||
| const cs_real_t | cofafp[], | ||
| const cs_real_t | cofbfp[], | ||
| const cs_real_t | i_massflux[], | ||
| const cs_real_t | b_massflux[], | ||
| const cs_real_t | i_viscm[], | ||
| const cs_real_t | b_viscm[], | ||
| const cs_real_t | i_visc[], | ||
| const cs_real_t | b_visc[], | ||
| cs_real_6_t | viscel[], | ||
| const cs_real_2_t | weighf[], | ||
| const cs_real_t | weighb[], | ||
| int | icvflb, | ||
| const int | icvfli[], | ||
| const cs_real_t | rovsdt[], | ||
| cs_real_t | smbrp[], | ||
| cs_real_t | pvar[], | ||
| cs_real_t | dpvar[], | ||
| const cs_real_t | xcpp[], | ||
| cs_real_t | eswork[] | ||
| ) |
This function solves an advection diffusion equation with source terms for one time step for the variable 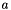 .
.
The equation reads:
![\[ f_s^{imp}(a^{n+1}-a^n) + \divs \left( a^{n+1} \rho \vect{u} - \mu \grad a^{n+1} \right) = Rhs \]](form_121.png)
This equation is rewritten as:
![\[ f_s^{imp} \delta a + \divs \left( \delta a \rho \vect{u} - \mu \grad \delta a \right) = Rhs^1 \]](form_122.png)
where 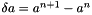 and
and 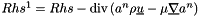
It is in fact solved with the following iterative process:
![\[ f_s^{imp} \delta a^k + \divs \left(\delta a^k \rho \vect{u}-\mu\grad\delta a^k \right) = Rhs^k \]](form_125.png)
where 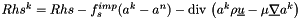
Be careful, it is forbidden to modify 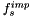 here!
here!
| [in] | idtvar | indicator of the temporal scheme |
| [in] | iterns | external sub-iteration number |
| [in] | f_id | field id (or -1) |
| [in] | iescap | compute the predictor indicator if 1 |
| [in] | imucpp | indicator
|
| [in] | normp | Reference norm to solve the system (optional) if negative: recomputed here |
| [in] | var_cal_opt | pointer to a cs_var_cal_opt_t structure which contains variable calculation options |
| [in] | pvara | variable at the previous time step 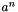 |
| [in] | pvark | variable at the previous sub-iteration 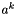 . If you sub-iter on Navier-Stokes, then it allows to initialize by something else than pvara (usually pvar=pvara) . If you sub-iter on Navier-Stokes, then it allows to initialize by something else than pvara (usually pvar=pvara) |
| [in] | coefap | boundary condition array for the variable (explicit part) |
| [in] | coefbp | boundary condition array for the variable (implicit part) |
| [in] | cofafp | boundary condition array for the diffusion of the variable (explicit part) |
| [in] | cofbfp | boundary condition array for the diffusion of the variable (implicit part) |
| [in] | i_massflux | mass flux at interior faces |
| [in] | b_massflux | mass flux at boundary faces |
| [in] | i_viscm | 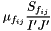 at interior faces for the matrix at interior faces for the matrix |
| [in] | b_viscm | 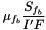 at boundary faces for the matrix at boundary faces for the matrix |
| [in] | i_visc | 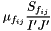 at interior faces for the r.h.s. at interior faces for the r.h.s. |
| [in] | b_visc | 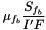 at boundary faces for the r.h.s. at boundary faces for the r.h.s. |
| [in] | viscel | symmetric cell tensor 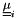 |
| [in] | weighf | internal face weight between cells i j in case of tensor diffusion |
| [in] | weighb | boundary face weight for cells i in case of tensor diffusion |
| [in] | icvflb | global indicator of boundary convection flux
|
| [in] | icvfli | boundary face indicator array of convection flux
|
| [in] | rovsdt | 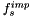 |
| [in] | smbrp | Right hand side 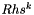 |
| [in,out] | pvar | current variable |
| [in,out] | dpvar | last variable increment |
| [in] | xcpp | array of specific heat (Cp) |
| [out] | eswork | prediction-stage error estimator (if iescap > 0) |
The equation reads:
![\[ f_s^{imp}(a^{n+1}-a^n) + \divs \left( a^{n+1} \rho \vect{u} - \mu \grad a^{n+1} \right) = Rhs \]](form_121.png)
This equation is rewritten as:
![\[ f_s^{imp} \delta a + \divs \left( \delta a \rho \vect{u} - \mu \grad \delta a \right) = Rhs^1 \]](form_122.png)
where 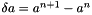 and
and 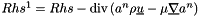
It is in fact solved with the following iterative process:
![\[ f_s^{imp} \delta a^k + \divs \left(\delta a^k \rho \vect{u}-\mu\grad\delta a^k \right) = Rhs^k \]](form_125.png)
where 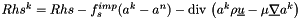
Be careful, it is forbidden to modify 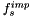 here!
here!
Please refer to the codits section of the theory guide for more informations.
| [in] | idtvar | indicator of the temporal scheme |
| [in] | iterns | external sub-iteration number |
| [in] | f_id | field id (or -1) |
| [in] | name | associated name if f_id < 0, or NULL |
| [in] | iescap | compute the predictor indicator if 1 |
| [in] | imucpp | indicator
|
| [in] | normp | Reference norm to solve the system (optional) if negative: recomputed here |
| [in] | var_cal_opt | pointer to a cs_var_cal_opt_t structure which contains variable calculation options |
| [in] | pvara | variable at the previous time step 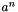 |
| [in] | pvark | variable at the previous sub-iteration 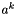 . If you sub-iter on Navier-Stokes, then it allows to initialize by something else than pvara (usually pvar=pvara) . If you sub-iter on Navier-Stokes, then it allows to initialize by something else than pvara (usually pvar=pvara) |
| [in] | coefap | boundary condition array for the variable (explicit part) |
| [in] | coefbp | boundary condition array for the variable (implicit part) |
| [in] | cofafp | boundary condition array for the diffusion of the variable (explicit part) |
| [in] | cofbfp | boundary condition array for the diffusion of the variable (implicit part) |
| [in] | i_massflux | mass flux at interior faces |
| [in] | b_massflux | mass flux at boundary faces |
| [in] | i_viscm | 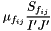 at interior faces for the matrix at interior faces for the matrix |
| [in] | b_viscm | 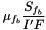 at boundary faces for the matrix at boundary faces for the matrix |
| [in] | i_visc | 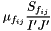 at interior faces for the r.h.s. at interior faces for the r.h.s. |
| [in] | b_visc | 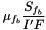 at boundary faces for the r.h.s. at boundary faces for the r.h.s. |
| [in] | viscel | symmetric cell tensor 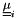 |
| [in] | weighf | internal face weight between cells i j in case of tensor diffusion |
| [in] | weighb | boundary face weight for cells i in case of tensor diffusion |
| [in] | icvflb | global indicator of boundary convection flux
|
| [in] | icvfli | boundary face indicator array of convection flux
|
| [in] | rovsdt | 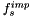 |
| [in] | smbrp | Right hand side 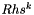 |
| [in,out] | pvar | current variable |
| [in,out] | dpvar | last variable increment |
| [in] | xcpp | array of specific heat (Cp) |
| [out] | eswork | prediction-stage error estimator (if iescap > 0) |
| void cs_equation_iterative_solve_tensor | ( | int | idtvar, |
| int | f_id, | ||
| const char * | name, | ||
| cs_var_cal_opt_t * | var_cal_opt, | ||
| const cs_real_6_t | pvara[], | ||
| const cs_real_6_t | pvark[], | ||
| const cs_real_6_t | coefats[], | ||
| const cs_real_66_t | coefbts[], | ||
| const cs_real_6_t | cofafts[], | ||
| const cs_real_66_t | cofbfts[], | ||
| const cs_real_t | i_massflux[], | ||
| const cs_real_t | b_massflux[], | ||
| const cs_real_t | i_viscm[], | ||
| const cs_real_t | b_viscm[], | ||
| const cs_real_t | i_visc[], | ||
| const cs_real_t | b_visc[], | ||
| cs_real_6_t | viscel[], | ||
| const cs_real_2_t | weighf[], | ||
| const cs_real_t | weighb[], | ||
| int | icvflb, | ||
| const int | icvfli[], | ||
| const cs_real_66_t | fimp[], | ||
| cs_real_6_t | smbrp[], | ||
| cs_real_6_t | pvar[] | ||
| ) |
This function solves an advection diffusion equation with source terms for one time step for the symmetric tensor variable 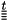 .
.
The equation reads:
![\[ \tens{f_s}^{imp}(\tens{\variat}^{n+1}-\tens{\variat}^n) + \divt \left( \tens{\variat}^{n+1} \otimes \rho \vect {u} - \mu \gradtt \tens{\variat}^{n+1}\right) = \tens{Rhs} \]](form_146.png)
This equation is rewritten as:
![\[ \tens{f_s}^{imp} \delta \tens{\variat} + \divt \left( \delta \tens{\variat} \otimes \rho \vect{u} - \mu \gradtt \delta \tens{\variat} \right) = \tens{Rhs}^1 \]](form_147.png)
where 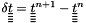 and
and 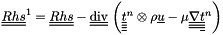
It is in fact solved with the following iterative process:
![\[ \tens{f_s}^{imp} \delta \tens{\variat}^k + \divt \left( \delta \tens{\variat}^k \otimes \rho \vect{u} - \mu \gradtt \delta \tens{\variat}^k \right) = \tens{Rhs}^k \]](form_150.png)
where 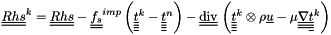
Be careful, it is forbidden to modify 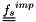 here!
here!
| [in] | idtvar | indicator of the temporal scheme |
| [in] | f_id | field id (or -1) |
| [in] | var_cal_opt | pointer to a cs_var_cal_opt_t structure which contains variable calculation options |
| [in] | pvara | variable at the previous time step 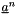 |
| [in] | pvark | variable at the previous sub-iteration 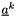 . If you sub-iter on Navier-Stokes, then it allows to initialize by something else than pvara (usually pvar=pvara) . If you sub-iter on Navier-Stokes, then it allows to initialize by something else than pvara (usually pvar=pvara) |
| [in] | coefats | boundary condition array for the variable (Explicit part) |
| [in] | coefbts | boundary condition array for the variable (Impplicit part) |
| [in] | cofafts | boundary condition array for the diffusion of the variable (Explicit part) |
| [in] | cofbfts | boundary condition array for the diffusion of the variable (Implicit part) |
| [in] | i_massflux | mass flux at interior faces |
| [in] | b_massflux | mass flux at boundary faces |
| [in] | i_viscm | 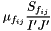 at interior faces for the matrix at interior faces for the matrix |
| [in] | b_viscm | 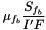 at boundary faces for the matrix at boundary faces for the matrix |
| [in] | i_visc | 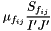 at interior faces for the r.h.s. at interior faces for the r.h.s. |
| [in] | b_visc | 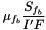 at boundary faces for the r.h.s. at boundary faces for the r.h.s. |
| [in] | viscel | symmetric cell tensor 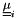 |
| [in] | weighf | internal face weight between cells i j in case of tensor diffusion |
| [in] | weighb | boundary face weight for cells i in case of tensor diffusion |
| [in] | icvflb | global indicator of boundary convection flux
|
| [in] | icvfli | boundary face indicator array of convection flux
|
| [in] | fimp | 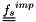 |
| [in] | smbrp | Right hand side 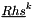 |
| [in,out] | pvar | current variable |
The equation reads:
![\[ \tens{f_s}^{imp}(\tens{\variat}^{n+1}-\tens{\variat}^n) + \divt \left( \tens{\variat}^{n+1} \otimes \rho \vect {u} - \mu \gradtt \tens{\variat}^{n+1}\right) = \tens{Rhs} \]](form_146.png)
This equation is rewritten as:
![\[ \tens{f_s}^{imp} \delta \tens{\variat} + \divt \left( \delta \tens{\variat} \otimes \rho \vect{u} - \mu \gradtt \delta \tens{\variat} \right) = \tens{Rhs}^1 \]](form_147.png)
where 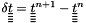 and
and 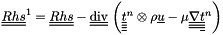
It is in fact solved with the following iterative process:
![\[ \tens{f_s}^{imp} \delta \tens{\variat}^k + \divt \left( \delta \tens{\variat}^k \otimes \rho \vect{u} - \mu \gradtt \delta \tens{\variat}^k \right) = \tens{Rhs}^k \]](form_150.png)
where 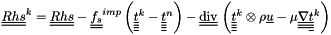
Be careful, it is forbidden to modify 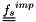 here!
here!
| [in] | idtvar | indicator of the temporal scheme |
| [in] | f_id | field id (or -1) |
| [in] | name | associated name if f_id < 0, or NULL |
| [in] | var_cal_opt | pointer to a cs_var_cal_opt_t structure which contains variable calculation options |
| [in] | pvara | variable at the previous time step 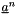 |
| [in] | pvark | variable at the previous sub-iteration 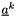 . If you sub-iter on Navier-Stokes, then it allows to initialize by something else than pvara (usually pvar=pvara) . If you sub-iter on Navier-Stokes, then it allows to initialize by something else than pvara (usually pvar=pvara) |
| [in] | coefats | boundary condition array for the variable (Explicit part) |
| [in] | coefbts | boundary condition array for the variable (Impplicit part) |
| [in] | cofafts | boundary condition array for the diffusion of the variable (Explicit part) |
| [in] | cofbfts | boundary condition array for the diffusion of the variable (Implicit part) |
| [in] | i_massflux | mass flux at interior faces |
| [in] | b_massflux | mass flux at boundary faces |
| [in] | i_viscm | 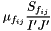 at interior faces for the matrix at interior faces for the matrix |
| [in] | b_viscm | 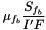 at boundary faces for the matrix at boundary faces for the matrix |
| [in] | i_visc | 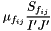 at interior faces for the r.h.s. at interior faces for the r.h.s. |
| [in] | b_visc | 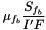 at boundary faces for the r.h.s. at boundary faces for the r.h.s. |
| [in] | viscel | symmetric cell tensor 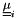 |
| [in] | weighf | internal face weight between cells i j in case of tensor diffusion |
| [in] | weighb | boundary face weight for cells i in case of tensor diffusion |
| [in] | icvflb | global indicator of boundary convection flux
|
| [in] | icvfli | boundary face indicator array of convection flux
|
| [in] | fimp | 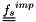 |
| [in] | smbrp | Right hand side 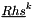 |
| [in,out] | pvar | current variable |
| void cs_equation_iterative_solve_vector | ( | int | idtvar, |
| int | iterns, | ||
| int | f_id, | ||
| const char * | name, | ||
| int | ivisep, | ||
| int | iescap, | ||
| cs_var_cal_opt_t * | var_cal_opt, | ||
| const cs_real_3_t | pvara[], | ||
| const cs_real_3_t | pvark[], | ||
| const cs_real_3_t | coefav[], | ||
| const cs_real_33_t | coefbv[], | ||
| const cs_real_3_t | cofafv[], | ||
| const cs_real_33_t | cofbfv[], | ||
| const cs_real_t | i_massflux[], | ||
| const cs_real_t | b_massflux[], | ||
| cs_real_t | i_viscm[], | ||
| const cs_real_t | b_viscm[], | ||
| const cs_real_t | i_visc[], | ||
| const cs_real_t | b_visc[], | ||
| const cs_real_t | i_secvis[], | ||
| const cs_real_t | b_secvis[], | ||
| cs_real_6_t | viscel[], | ||
| const cs_real_2_t | weighf[], | ||
| const cs_real_t | weighb[], | ||
| int | icvflb, | ||
| const int | icvfli[], | ||
| const cs_real_33_t | fimp[], | ||
| cs_real_3_t | smbrp[], | ||
| cs_real_3_t | pvar[], | ||
| cs_real_3_t | eswork[] | ||
| ) |
This function solves an advection diffusion equation with source terms for one time step for the vector variable 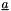 .
.
The equation reads:
![\[ \tens{f_s}^{imp}(\vect{a}^{n+1}-\vect{a}^n) + \divv \left( \vect{a}^{n+1} \otimes \rho \vect {u} - \mu \gradt \vect{a}^{n+1}\right) = \vect{Rhs} \]](form_134.png)
This equation is rewritten as:
![\[ \tens{f_s}^{imp} \delta \vect{a} + \divv \left( \delta \vect{a} \otimes \rho \vect{u} - \mu \gradt \delta \vect{a} \right) = \vect{Rhs}^1 \]](form_135.png)
where 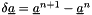 and
and 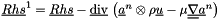
It is in fact solved with the following iterative process:
![\[ \tens{f_s}^{imp} \delta \vect{a}^k + \divv \left( \delta \vect{a}^k \otimes \rho \vect{u} - \mu \gradt \delta \vect{a}^k \right) = \vect{Rhs}^k \]](form_138.png)
where 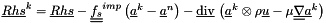
Be careful, it is forbidden to modify 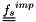 here!
here!
| [in] | idtvar | indicator of the temporal scheme |
| [in] | iterns | external sub-iteration number |
| [in] | f_id | field id (or -1) |
| [in] | name | associated name if f_id < 0, or NULL |
| [in] | ivisep | indicator to take 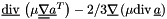
|
| [in] | iescap | compute the predictor indicator if 1 |
| [in] | var_cal_opt | pointer to a cs_var_cal_opt_t structure which contains variable calculation options |
| [in] | pvara | variable at the previous time step 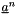 |
| [in] | pvark | variable at the previous sub-iteration 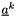 . If you sub-iter on Navier-Stokes, then it allows to initialize by something else than pvara (usually pvar=pvara) . If you sub-iter on Navier-Stokes, then it allows to initialize by something else than pvara (usually pvar=pvara) |
| [in] | coefav | boundary condition array for the variable (explicit part) |
| [in] | coefbv | boundary condition array for the variable (implicit part) |
| [in] | cofafv | boundary condition array for the diffusion of the variable (Explicit part) |
| [in] | cofbfv | boundary condition array for the diffusion of the variable (Implicit part) |
| [in] | i_massflux | mass flux at interior faces |
| [in] | b_massflux | mass flux at boundary faces |
| [in] | i_viscm | 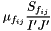 at interior faces for the matrix at interior faces for the matrix |
| [in] | b_viscm | 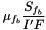 at boundary faces for the matrix at boundary faces for the matrix |
| [in] | i_visc | 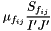 at interior faces for the r.h.s. at interior faces for the r.h.s. |
| [in] | b_visc | 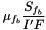 at boundary faces for the r.h.s. at boundary faces for the r.h.s. |
| [in] | i_secvis | secondary viscosity at interior faces |
| [in] | b_secvis | secondary viscosity at boundary faces |
| [in] | viscel | symmetric cell tensor 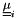 |
| [in] | weighf | internal face weight between cells i j in case of tensor diffusion |
| [in] | weighb | boundary face weight for cells i in case of tensor diffusion |
| [in] | icvflb | global indicator of boundary convection flux
|
| [in] | icvfli | boundary face indicator array of convection flux
|
| [in] | fimp | 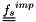 |
| [in] | smbrp | Right hand side 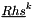 |
| [in,out] | pvar | current variable |
| [out] | eswork | prediction-stage error estimator (if iescap > 0) |
The equation reads:
![\[ \tens{f_s}^{imp}(\vect{a}^{n+1}-\vect{a}^n) + \divv \left( \vect{a}^{n+1} \otimes \rho \vect {u} - \mu \gradt \vect{a}^{n+1}\right) = \vect{Rhs} \]](form_134.png)
This equation is rewritten as:
![\[ \tens{f_s}^{imp} \delta \vect{a} + \divv \left( \delta \vect{a} \otimes \rho \vect{u} - \mu \gradt \delta \vect{a} \right) = \vect{Rhs}^1 \]](form_135.png)
where 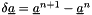 and
and 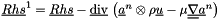
It is in fact solved with the following iterative process:
![\[ \tens{f_s}^{imp} \delta \vect{a}^k + \divv \left( \delta \vect{a}^k \otimes \rho \vect{u} - \mu \gradt \delta \vect{a}^k \right) = \vect{Rhs}^k \]](form_138.png)
where 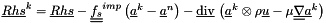
Be careful, it is forbidden to modify 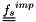 here!
here!
| [in] | idtvar | indicator of the temporal scheme |
| [in] | iterns | external sub-iteration number |
| [in] | f_id | field id (or -1) |
| [in] | name | associated name if f_id < 0, or NULL |
| [in] | ivisep | indicator to take 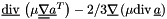
|
| [in] | iescap | compute the predictor indicator if 1 |
| [in] | var_cal_opt | pointer to a cs_var_cal_opt_t structure which contains variable calculation options |
| [in] | pvara | variable at the previous time step 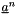 |
| [in] | pvark | variable at the previous sub-iteration 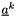 . If you sub-iter on Navier-Stokes, then it allows to initialize by something else than pvara (usually pvar= pvara) . If you sub-iter on Navier-Stokes, then it allows to initialize by something else than pvara (usually pvar= pvara) |
| [in] | coefav | boundary condition array for the variable (explicit part) |
| [in] | coefbv | boundary condition array for the variable (implicit part) |
| [in] | cofafv | boundary condition array for the diffusion of the variable (Explicit part) |
| [in] | cofbfv | boundary condition array for the diffusion of the variable (Implicit part) |
| [in] | i_massflux | mass flux at interior faces |
| [in] | b_massflux | mass flux at boundary faces |
| [in] | i_viscm | 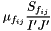 at interior faces for the matrix at interior faces for the matrix |
| [in] | b_viscm | 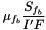 at boundary faces for the matrix at boundary faces for the matrix |
| [in] | i_visc | 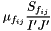 at interior faces for the r.h.s. at interior faces for the r.h.s. |
| [in] | b_visc | 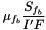 at boundary faces for the r.h.s. at boundary faces for the r.h.s. |
| [in] | i_secvis | secondary viscosity at interior faces |
| [in] | b_secvis | secondary viscosity at boundary faces |
| [in] | viscel | symmetric cell tensor 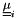 |
| [in] | weighf | internal face weight between cells i j in case of tensor diffusion |
| [in] | weighb | boundary face weight for cells i in case of tensor diffusion |
| [in] | icvflb | global indicator of boundary convection flux
|
| [in] | icvfli | boundary face indicator array of convection flux
|
| [in] | fimp | 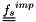 |
| [in] | smbrp | Right hand side 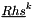 |
| [in,out] | pvar | current variable |
| [out] | eswork | prediction-stage error estimator (if iescap > 0) |
 1.8.16
1.8.16