Functions/Subroutines
subroutine	cavitation_model_init
	Initialize Fortran cavitation model API. This maps Fortran pointers to global C structure members and indicator. More...

subroutine	cavitation_compute_source_term (pressure, voidf)
	Compute the vaporization source term 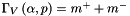$\Gamma_V \left(\alpha, p\right) = m^+ + m^-$ using the Merkle model: More...

subroutine	cavitation_correct_visc_turb (crom, voidf, visct)
	Modify eddy viscosity using the Reboud correction: More...

Variables
real(c_double), pointer, save	presat
	reference saturation pressure (kg/(m s2)) More...

real(c_double), pointer, save	uinf
	reference velocity of the flow (m/s) More...

real(c_double), pointer, save	linf
	reference length scale of the flow (m) More...

real(c_double), pointer, save	cdest
	constant Cdest of the condensation source term (Merkle model) More...

real(c_double), pointer, save	cprod
	constant Cprod of the vaporization source term (Merkle model) More...

integer(c_int), pointer, save	icvevm
	activation of the eddy-viscosity correction (Reboud correction) More...

real(c_double), pointer, save	mcav
	constant mcav of the eddy-viscosity correction (Reboud correction) More...

integer(c_int), pointer, save	itscvi
	implicitation in pressure of the vaporization/condensation model More...

Function/Subroutine Documentation

◆ cavitation_compute_source_term()

subroutine cavitation::cavitation_compute_source_term	(	double precision, dimension(ncelet)	pressure,
		double precision, dimension(ncelet)	voidf
	)

Compute the vaporization source term 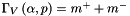$\Gamma_V \left(\alpha, p\right) = m^+ + m^-$ using the Merkle model:

$m^+ = -\dfrac{C_{prod} \rho_l \min \left( p-p_V,0 \right)\alpha(1-\alpha)} {0.5\rho_lu_\infty^2t_\infty},$

$m^- = -\dfrac{C_{dest} \rho_v \max \left( p-p_V,0 \right)\alpha(1-\alpha)} {0.5\rho_lu_\infty^2t_\infty},$

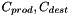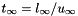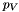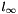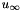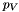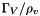with $C_{prod}, C_{dest}$ empirical constants, $t_\infty=l_\infty/u_\infty$ a reference time scale and $p_V$ the reference saturation pressure. $l_\infty$ , $u_\infty$ and $p_V$ may be provided by the user (user function). Note that the r.h.s. of the void fraction transport equation is $\Gamma_V/\rho_v$ .

Parameters

[in]	pressure	Pressure array
[in]	voidf	Void fraction array

◆ cavitation_correct_visc_turb()

subroutine cavitation::cavitation_correct_visc_turb	(	double precision, dimension(ncelet)	crom,
		double precision, dimension(ncelet)	voidf,
		double precision, dimension(ncelet)	visct
	)

Modify eddy viscosity using the Reboud correction:

$\mu_t'= \dfrac{\rho_v + (1-\alpha)^{mcav}(\rho_l-\rho_v)}{\rho}\mu_t.$

Parameters

[in]	crom	density array
[in]	voidf	void fraction array
[in,out]	visct	turbulent viscosity

◆ cavitation_model_init()

subroutine cavitation::cavitation_model_init ( )

Initialize Fortran cavitation model API. This maps Fortran pointers to global C structure members and indicator.

Functions/Subroutines

Variables

Function/Subroutine Documentation

◆ cavitation_compute_source_term()

◆ cavitation_correct_visc_turb()

◆ cavitation_model_init()