|
My Project
programmer's documentation
|
|
My Project
programmer's documentation
|
This page provides code blocks of several examples that may be used to perform fluid structure interaction computations.
The lstelt array is allocated.
The following code block provides an example of definition of two internal structures.
Here one fills array idfstr(nfabor). For each boundary face ifac, idfstr(ifac) is the number of the structure the face belongs to (if idfstr(ifac) = 0, the face ifac doesn't belong to any structure. When using internal coupling, structure number necessarily needs to be positive (as shown in following examples).
The number of "internal" structures is automatically defined with the maximum value of idfstr table, meaning that internal structure numbers must be defined sequentially with positive values, beginning with integer value 1.
In the following example, boundary faces with color 4 belong to internal structure 1. Boundary faces with color 2 belong to internal structure 2. The total number of internal structures equals 2. The boundary faces are identified using the getfbr subroutine.
For each internal structure one can here define :
vstr0 xstr0 (i.e. xstr0 is the value of the displacement xstr compared to the initial mesh at time t=0)\ref xstreq. \ref xstreq is the initial displacement of the internal structure compared to its position at equilibrium; at each time step t and for a displacement xstr(t), the associated internal structure will be subjected to a force due to the spring:
![\[ -k (xstr(t)+xstreq). \]](form_670.png)
Note that xstr0, \ref xstreq and vstr0 arrays are initialized at the beginning of the calculations to the value of 0.
When starting a calculation using ALE, or re-starting a calculation with ALE basing on a first calculation without ALE, an initial iteration 0 is automatically calculated in order to take initial arrays xstr0, vstr0 and \ref xstreq into account. In another case, set the following option
in subroutine usipsu, so that the code can deal with arrays xstr0, vstr0 or \ref xstreq.
In the following example :
xstr0 of 2 meters in the y direction and a displacement compared to equilibrium \ref xstreq of 1 meter in the y direction.vstr0 in the z direction of structure 2 equals -0.5 m/s.Here one can modify the values of the prediction coefficients for displacements anf fluid forces in internal FSI coupled algorithm.
The use of these coefficients is reminded here :
![\[ \vect{X_{n+1}} = \vect{X_n} + aexxst \Delta t \vect{X^{\prime}_n} + bexxst \Delta t (\vect{X^{\prime}_n}-\vect{X^{\prime}_{n-1}}) \]](form_671.png)
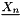 standing for the displacement at iteration
standing for the displacement at iteration 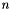 ,
, 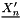 and
and 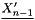 representing the internal structure velocity respectively at iteration
representing the internal structure velocity respectively at iteration 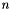 and
and  .
.
![\[ \vect{F_{n+1}} = cfopre \vect{F_n} + (1-cfopre) \vect{F_{n-1}} \]](form_677.png)
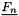 and
and 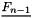 standing for the fluid force acting on the structure respectively at iteration
standing for the fluid force acting on the structure respectively at iteration 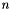 and
and  .
. Activation of structural history output (i.e. displacement, structural velocity, structural acceleration and fluid force) (ihistr=0, disabled ; ihistr=1, enabled) The value of structural history output step is the same as the one for standard variables (nthist).
Note that the subroutine usstr2 is called at each time step of the calculation.
For each internal structure one defines here :
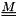 (
(xmstru)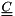 (
(xcstru)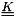 (
(xkstru)forstr array gives fluid stresses acting on each internal structure. Moreover it's possible to take external forces (gravity for example) into account, too.
\ref xstr array indicates the displacement of the structure compared to its position in the initial mesh.
xstr0 array gives the displacement of the structures in initial mesh compared to structural equilibrium.
\ref vstr array stands for structural velocity.
\ref xstr, xstr0, and \ref vstr arrays are data tables that can be used to define arrays mass, friction and stiffness. THOSE ARE NOT TO BE MODIFIED.
The 3D structural equation that is solved is the following one :
![\[ \tens{M} \vect{X^{\prime\prime}} + \tens{C} \vect{X^{\prime}} + \tens{K} (\vect{X}+\vect{X_0}) = \vect{F} \]](form_683.png)
where 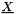 stands for the structural displacement compared to initial mesh position (
stands for the structural displacement compared to initial mesh position (\ref xstr) and 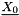 represents the displacement of the structure in initial mesh compared to equilibrium.
represents the displacement of the structure in initial mesh compared to equilibrium.
Note that 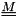 ,
, 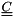 and
and 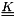 are 3x3 matrices.
are 3x3 matrices.
This equation is solved using a Newmark HHT algorithm. Note that the time step used to solve this equation (dtstr) can be different from the one of fluid calculations. user is free to define dtstr array. At the beginning of the calculation dtstr is initialized to the value of \ref dt (fluid time step).
The matrices xmstru, xcstru and xkstru are set to zero.
Two examples of definition of the mass, the friction coefficient and the stiffness of an internal structure are provided hereafter.
The lstelt array is allocated.
In the following example, two sets of boundary faces that will be coupled with Code_Aster are defined as well as the fluid force components which are given to structural calculations.
Here one fills array idfstr(nfabor) For each boundary face ifac, idfstr(ifac) is the number of the structure the face belongs to (if idfstr(ifac) = 0, the face ifac doesn't belong to any structure.) When using external coupling with Code_Aster, structure number necessarily needs to be negative (as shown in following examples).
The number of "external" structures with Code_Aster is automatically defined with the maximum absolute value of idfstr table, meaning that external structure numbers must be defined sequentially with negative values beginning with integer value -1.
In following example, boundary faces with color 2 and which abscissa 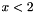 belong to external structure -1. Boundary faces with color 2 and which abscissa
belong to external structure -1. Boundary faces with color 2 and which abscissa 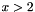 belong to external structure -2. The total number of external structures coupled with Code_Aster equals 2.
belong to external structure -2. The total number of external structures coupled with Code_Aster equals 2.
 1.8.16
1.8.16