Energy balance
Local variables to be added
The following local variables need to be defined for the examples in this section:
integer iel , ifac , ivar
integer iel1 , iel2 , ieltsm
integer iortho
integer inc , iccocg
integer iflmas , iflmab , ipccp
integer iscal
integer ilelt , nlelt
double precision xvara , xvar
double precision xbilan , xbilvl , xbilpa , xbilpt
double precision xbilsy , xbilen , xbilso , xbildv
double precision xbilmi , xbilma
double precision xfluxf , xgamma
double precision flumab , ctb1, ctb2
integer, allocatable, dimension(:) :: lstelt
double precision, allocatable, dimension(:,:) :: grad
double precision, allocatable, dimension(:) :: treco
double precision, allocatable, dimension(:) :: xcp
double precision, dimension(:), pointer :: imasfl, bmasfl
double precision, dimension(:), pointer :: coefap, coefbp, cofafp, cofbfp
double precision, dimension(:), pointer :: crom
double precision, dimension(:), pointer :: cpro_visct, cpro_cp
double precision, dimension(:), pointer :: cvar_scal, cvara_scal
Initialization and finalization
The following initialization block needs to be added for the following examples:
allocate(lstelt(max(ncel,nfac,nfabor)))
allocate(xcp(ncel))
Ad the end of the subroutine, it is recommended to deallocate the work array:
deallocate(lstelt)
deallocate(xcp)
In theory Fortran 95 deallocates locally-allocated arrays automatically, but deallocating arrays in a symmetric manner to their allocation is good practice, and it avoids using a different logic for C and Fortran.
Body
This example computes energy balance relative to temperature We assume that we want to compute balances (convective and diffusive) at the boundaries of the calculation domain represented below (with boundaries marked by colors).
The scalar considered if the temperature. We will also use the specific heat (to obtain balances in Joules)
Domain and associated boundary colors:
- 2, 4, 7 : adiabatic walls
- 6 : wall with fixed temperature
- 3 : inlet
- 5 : outlet
- 1 : symmetry
To ensure calculations have physical meaning, it is best to use a spatially uniform time step (idtvar = 0 or 1). In addition, when restarting a calculation, the balance may be incorrect at the first time step.
Temperature variable
Boundary coefficients coefap/coefbp are those of ivarfl(ivar).
The balance at time step n is equal to:
![\[ \begin{array}{r c l} Balance^n &=& \displaystyle \sum_{\celli=1}^{\ncell} \norm{\vol{\celli}} C_p \rho_\celli \left(T_\celli^{n-1} -T_\celli^n \right) \\ &+& \displaystyle \sum_{\fib} C_p \Delta t_\celli \norm{\vect{S}_\ib} \left(A_\ib^f + B_\ib^f T_\celli^n \right) \\ &+& \displaystyle \sum_{\fib} C_p \Delta t_\celli \dot{m}_\ib \left(A_\ib^g + B_\ib^g T_\celli^n \right) \end{array} \]](form_655.png)
The first term is negative if the amount of energy in the volume has increased (it is 0 in a steady regime).
The other terms (convection, diffusion) are positive if the amount of energy in the volume has increased due to boundary conditions.
In a steady regime, a positive balance thus indicates an energy gain.
With 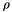 (
(rom) calculated using the density law from the usphyv subroutine, for example:
![\[ \rho^{n-1}_\celli = P_0 / \left( R T_\celli^{n-1} + T_0 \right) \]](form_656.png)
where 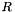 is
is cs_physical_constants_r and 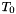 is
is tkelv.
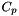 and
and 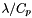 may vary.
may vary.
Here is the corresponding code:
if (ntcabs.eq.ntpabs) then
xbilvl = 0.d0
xbildv = 0.d0
xbilpa = 0.d0
xbilpt = 0.d0
xbilsy = 0.d0
xbilen = 0.d0
xbilso = 0.d0
xbilmi = 0.d0
xbilma = 0.d0
xbilan = 0.d0
iscal = iscalt
ivar = isca(iscal)
call field_get_val_s(ivarfl(ivar), cvar_scal)
call field_get_val_prev_s(ivarfl(ivar), cvara_scal)
call field_get_val_s(icrom, crom)
call field_get_val_s(ivisct, cpro_visct)
call field_get_key_int(ivarfl(ivar), kimasf, iflmas)
call field_get_key_int(ivarfl(ivar), kbmasf, iflmab)
call field_get_val_s(iflmas, imasfl)
call field_get_val_s(iflmab, bmasfl)
if (icp.ge.0) call field_get_val_s(icp, cpro_cp)
if (itherm.eq.1) then
if (icp.ge.0) then
do iel = 1, ncel
xcp(iel) = cpro_cp(iel)
enddo
else
do iel = 1, ncel
xcp(iel) = cp0
enddo
endif
else
do iel = 1, ncel
xcp(iel) = 1.d0
enddo
endif
call field_get_coefa_s(ivarfl(ivar), coefap)
call field_get_coefb_s(ivarfl(ivar), coefbp)
call field_get_coefaf_s(ivarfl(ivar), cofafp)
call field_get_coefbf_s(ivarfl(ivar), cofbfp)
allocate(treco(nfabor))
iortho = 0
if (iortho.eq.0) then
allocate(grad(3,ncelet))
inc = 1
iccocg = 1
call field_gradient_scalar &
(ivarfl(ivar), 0, imrgra, inc, iccocg, &
grad)
do ifac = 1, nfabor
iel = ifabor(ifac)
treco(ifac) = cvar_scal(iel) &
+ diipb(1,ifac)*grad(1,iel) &
+ diipb(2,ifac)*grad(2,iel) &
+ diipb(3,ifac)*grad(3,iel)
enddo
deallocate(grad)
else
do ifac = 1, nfabor
iel = ifabor(ifac)
treco(ifac) = cvar_scal(iel)
enddo
endif
do iel = 1, ncel
xvara = cvara_scal(iel)
xvar = cvar_scal(iel)
xbilvl = xbilvl &
+ volume(iel) * xcp(iel) * crom(iel) &
* (xvara - xvar)
enddo
do ifac = 1, nfac
iel1 = ifacel(1,ifac)
if (iel1.le.ncel) then
ctb1 = imasfl(ifac)*xcp(iel1)*cvar_scal(iel1)*
dt(iel1)
else
ctb1 = 0d0
endif
iel2 = ifacel(2,ifac)
if (iel2.le.ncel) then
ctb2 = imasfl(ifac)*xcp(iel2)*cvar_scal(iel2)*
dt(iel2)
else
ctb2 = 0d0
endif
xbildv = xbildv + (ctb1 - ctb2)
enddo
do ifac = 1, nfabor
iel = ifabor(ifac)
xbildv = xbildv +
dt(iel) * xcp(iel) &
* bmasfl(ifac) &
* cvar_scal(iel)
enddo
if (ncetsm.gt.0) then
do ieltsm = 1, ncetsm
iel = icetsm(ieltsm)
xvar = cvar_scal(iel)
xgamma = smacel(ieltsm,ipr)
xbildv = xbildv &
- volume(iel) * xcp(iel) *
dt(iel) &
* xgamma * xvar
enddo
endif
call getfbr(
'2 or 4 or 7', nlelt, lstelt)
do ilelt = 1, nlelt
ifac = lstelt(ilelt)
iel = ifabor(ifac)
flumab = bmasfl(ifac)
xfluxf = - surfbn(ifac) *
dt(iel) &
* (cofafp(ifac) + cofbfp(ifac)*treco(ifac)) &
- flumab *
dt(iel) * xcp(iel) &
* (coefap(ifac) + coefbp(ifac)*treco(ifac))
xbilpa = xbilpa + xfluxf
enddo
call getfbr(
'6', nlelt, lstelt)
do ilelt = 1, nlelt
ifac = lstelt(ilelt)
iel = ifabor(ifac)
flumab = bmasfl(ifac)
xfluxf = - surfbn(ifac) *
dt(iel) &
* (cofafp(ifac) + cofbfp(ifac)*treco(ifac)) &
- flumab *
dt(iel) * xcp(iel) &
* (coefap(ifac) + coefbp(ifac)*treco(ifac))
xbilpt = xbilpt + xfluxf
enddo
call getfbr(
'1', nlelt, lstelt)
do ilelt = 1, nlelt
ifac = lstelt(ilelt)
iel = ifabor(ifac)
flumab = bmasfl(ifac)
xfluxf = - surfbn(ifac) *
dt(iel) &
* (cofafp(ifac) + cofbfp(ifac)*treco(ifac)) &
- flumab *
dt(iel) * xcp(iel) &
* (coefap(ifac) + coefbp(ifac)*treco(ifac))
xbilsy = xbilsy + xfluxf
enddo
call getfbr(
'3', nlelt, lstelt)
do ilelt = 1, nlelt
ifac = lstelt(ilelt)
iel = ifabor(ifac)
flumab = bmasfl(ifac)
xfluxf = - surfbn(ifac) *
dt(iel) &
* (cofafp(ifac) + cofbfp(ifac)*treco(ifac)) &
- flumab *
dt(iel) * xcp(iel) &
* (coefap(ifac) + coefbp(ifac)*treco(ifac))
xbilen = xbilen + xfluxf
enddo
call getfbr(
'5', nlelt, lstelt)
do ilelt = 1, nlelt
ifac = lstelt(ilelt)
iel = ifabor(ifac)
flumab = bmasfl(ifac)
xfluxf = - surfbn(ifac) *
dt(iel) &
* (cofafp(ifac) + cofbfp(ifac)*treco(ifac)) &
- flumab *
dt(iel) * xcp(iel) &
* (coefap(ifac) + coefbp(ifac)*treco(ifac))
xbilso = xbilso + xfluxf
enddo
deallocate(treco)
if (ncetsm.gt.0) then
do ieltsm = 1, ncetsm
iel = icetsm(ieltsm)
xgamma = smacel(ieltsm,ipr)
if (itypsm(ieltsm,ivar).eq.0 .or. xgamma.lt.0.d0) then
xvar = cvar_scal(iel)
else
xvar = smacel(ieltsm,ivar)
endif
if (icp.ge.0) then
if (xgamma.lt.0.d0) then
xbilma = xbilma &
+ volume(iel) * cpro_cp(iel) *
dt(iel) * xgamma * xvar
else
xbilmi = xbilmi &
+ volume(iel) * cpro_cp(iel) *
dt(iel) * xgamma * xvar
endif
else
if (xgamma.lt.0.d0) then
xbilma = xbilma &
+ volume(iel) * cp0 *
dt(iel) * xgamma * xvar
else
xbilmi = xbilmi &
+ volume(iel) * cp0 *
dt(iel) * xgamma * xvar
endif
endif
enddo
endif
if (irangp.ge.0) then
call parsom(xbilvl)
call parsom(xbildv)
call parsom(xbilpa)
call parsom(xbilpt)
call parsom(xbilsy)
call parsom(xbilen)
call parsom(xbilso)
call parsom(xbilmi)
call parsom(xbilma)
endif
xbilan = xbilvl + xbildv + xbilpa + xbilpt + xbilsy + xbilen &
+ xbilso + xbilmi + xbilma
write (nfecra, 2000) &
ntcabs, xbilvl, xbildv, xbilpa, xbilpt, xbilsy, xbilen, xbilso, &
xbilmi, xbilma, xbilan
2000 format &
(/, &
3x,'** Thermal balance **', /, &
3x,' ---------------', /, &
'---', '------', &
'------------------------------------------------------------', /, &
'bt ',' Iter', &
' Volume Divergence Adia Wall Fixed_T Wall Symmetry', &
' Inlet Outlet Inj. Mass. Suc. Mass. Total', /, &
'bt ', i6, 10e12.4, /, &
'---','------', &
'------------------------------------------------------------')
endif
![\[ \begin{array}{r c l} Balance^n &=& \displaystyle \sum_{\celli=1}^{\ncell} \norm{\vol{\celli}} C_p \rho_\celli \left(T_\celli^{n-1} -T_\celli^n \right) \\ &+& \displaystyle \sum_{\fib} C_p \Delta t_\celli \norm{\vect{S}_\ib} \left(A_\ib^f + B_\ib^f T_\celli^n \right) \\ &+& \displaystyle \sum_{\fib} C_p \Delta t_\celli \dot{m}_\ib \left(A_\ib^g + B_\ib^g T_\celli^n \right) \end{array} \]](form_655.png)
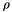 (
(![\[ \rho^{n-1}_\celli = P_0 / \left( R T_\celli^{n-1} + T_0 \right) \]](form_656.png)
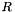 is
is 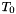 is
is 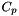 and
and 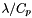 may vary.
may vary. 1.8.16
1.8.16