My Project
programmer's documentation
Typedefs | Enumerations | Functions
cs_sles_pc.h File Reference
#include "cs_base.h"
#include "cs_log.h"
#include "cs_halo_perio.h"
#include "cs_matrix.h"
Include dependency graph for cs_sles_pc.h:

Go to the source code of this file.

Typedefs

typedef struct _cs_sles_pc_t cs_sles_pc_t
 
typedef void() cs_sles_pc_setup_t(void *context, const char *name, const cs_matrix_t *a, int verbosity)
 Function pointer for pre-resolution setup of a preconditioner context. More...
 
typedef void() cs_sles_pc_tolerance_t(void *context, double precision, double r_norm)
 Function pointer for setting of the required tolerance for preconditioners involving an iterative solver. More...
 
typedef cs_sles_pc_state_t() cs_sles_pc_apply_t(void *context, cs_halo_rotation_t rotation_mode, const cs_real_t *x_in, cs_real_t *x_out)
 Function pointer for application of a preconditioner. More...
 
typedef void() cs_sles_pc_free_t(void *context)
 Function pointer for freeing of a preconditioner's context data. More...
 
typedef void() cs_sles_pc_log_t(const void *context, cs_log_t log_type)
 Function pointer for logging of preconditioner history and performance data. More...
 
typedef void *() cs_sles_pc_clone_t(const void *context)
 Function pointer for creation of a preconditioner context based on the copy of another. More...
 
typedef void() cs_sles_pc_destroy_t(void **context)
 

Enumerations

enum  cs_sles_pc_state_t { CS_SLES_PC_DIVERGED = -2, CS_SLES_PC_BREAKDOWN = -1, CS_SLES_PC_MAX_ITERATION = 0, CS_SLES_PC_CONVERGED = 1 }
 Convergence status indicator. More...
 

Functions

const typedef char *() cs_sles_pc_get_type_t (const void *context, bool logging)
 
void cs_sles_pc_log (cs_sles_pc_t *pc, cs_log_t log_type)
 Log preconditioner setup, history and performance data. More...
 
cs_sles_pc_t * cs_sles_pc_define (void *context, cs_sles_pc_get_type_t *get_type_func, cs_sles_pc_setup_t *setup_func, cs_sles_pc_tolerance_t *tolerance_func, cs_sles_pc_apply_t *apply_func, cs_sles_pc_free_t *free_func, cs_sles_pc_log_t *log_func, cs_sles_pc_clone_t *clone_func, cs_sles_pc_destroy_t *destroy_func)
 Define sparse linear equation preconditioner. More...
 
void cs_sles_pc_destroy (cs_sles_pc_t **pc)
 Destroy a sparse linear equation preconditioner. More...
 
cs_sles_pc_t * cs_sles_pc_clone (const cs_sles_pc_t *src)
 Create a new preconditioner context based on the copy of another. More...
 
const char * cs_sles_pc_get_type (cs_sles_pc_t *pc)
 Return type name of preconditioner context. More...
 
const char * cs_sles_pc_get_type_name (cs_sles_pc_t *pc)
 Return type name of preconditioner context. More...
 
void * cs_sles_pc_get_context (cs_sles_pc_t *pc)
 Return pointer to preconditioner context structure pointer. More...
 
cs_sles_pc_apply_t * cs_sles_pc_get_apply_func (const cs_sles_pc_t *pc)
 Return a pointer to the function used to apply a preconditioner. More...
 
void cs_sles_pc_set_tolerance (cs_sles_pc_t *pc, double precision, double r_norm)
 Set the required tolerance for preconditioners involving an iterative solver. More...
 
void cs_sles_pc_setup (cs_sles_pc_t *pc, const char *name, const cs_matrix_t *a, int verbosity)
 Setup sparse linear equation preconditioner. More...
 
cs_sles_pc_state_t cs_sles_pc_apply (cs_sles_pc_t *pc, cs_halo_rotation_t rotation_mode, cs_real_t *x_in, cs_real_t *x_out)
 Apply a preconditioner. More...
 
void cs_sles_pc_free (cs_sles_pc_t *pc)
 Free preconditioner setup. More...
 
cs_sles_pc_t * cs_sles_pc_none_create (void)
 Create an "identity" (or null) preconditioner. More...
 
cs_sles_pc_t * cs_sles_pc_jacobi_create (void)
 Create a Jacobi preconditioner. More...
 
cs_sles_pc_t * cs_sles_pc_poly_1_create (void)
 Create a polynomial preconditioner of degree 1. More...
 
cs_sles_pc_t * cs_sles_pc_poly_2_create (void)
 Create a polynomial preconditioner of degree 2. More...
 

Typedef Documentation

◆ cs_sles_pc_apply_t

cs_sles_pc_apply_t

Function pointer for application of a preconditioner.

In cases where it is desired that the preconditioner modify a vector "in place", x_in should be set to NULL, and x_out contain the vector to be modified ( 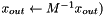$x_{out} \leftarrow M^{-1}x_{out})$).

Parameters
[in,out]contextpointer to solver context
[in]rotation_modehalo update option for rotational periodicity
[in]x_ininput vector
[in,out]x_outinput/output vector
Returns
preconditioner convergence status

◆ cs_sles_pc_clone_t

cs_sles_pc_clone_t

Function pointer for creation of a preconditioner context based on the copy of another.

The new context copies the settings of the copied context, but not its setup data and logged info, such as performance data.

This type of function is optional, but enables associating different preconditioners to related systems (to differentiate logging) while using the same settings by default.

Parameters
[in]contextcontext to clone
Returns
pointer to newly created context

◆ cs_sles_pc_destroy_t

cs_sles_pc_destroy_t

Function pointer for destruction of a preconditioner context.

This function should free all context data, and will be called for each system when cs_sles_finalize is called.

Parameters
[in,out]contextpointer to preconditioner context

Simple preconditioners also provided include:

  • identity (null)
  • Jacobi
  • polynomial of degree 1
  • polynomial of degree 2

Polynomial preconditioning is explained here: D being the diagonal part of matrix A and X its extra-diagonal part, it can be written 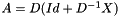$A=D(Id+D^{-1}X)$. Therefore 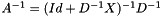$A^{-1}=(Id+D^{-1}X)^{-1}D^{-1}$. A series development of 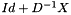$Id+D^{-1}X$ can then be used which yields, symbolically,

\[ Id+\sum\limits_{I=1}^{poly\_degree}\left(-D^{-1}X\right)^{I} \]

The Jacobi preconditioning is a polynomial preconditioning of degree 0.

The efficiency of the polynomial preconditioning will vary depending on the system type. In most cases, Jacobi or degree 1 provide best results. Each polynomial preconditioning degree above 0 adds one matrix-vector product per inital matrix-vector product of the algorithm. Switching from diagonal to polynomial degree 1 often divides the number of required iterations by approximately 2, but each iteration then costs close to 2 times that of diagonal preconditoning (other vector operations are not doubled), so the net gain is often about 10%. Higher degree polynomials usually lead to diminishing returns, so to avoid the need for additional parameter setting functions, only degrees 1 and 2 are provided here.

◆ cs_sles_pc_free_t

cs_sles_pc_free_t

Function pointer for freeing of a preconditioner's context data.

Note that this function should free resolution-related data, such as multigrid hierarchy and any other temporary arrays or objects required for application, but should not free the whole context, as info used for logging (especially performance data) should be maintained.

Parameters
[in,out]contextpointer to solver context.

◆ cs_sles_pc_log_t

cs_sles_pc_log_t

Function pointer for logging of preconditioner history and performance data.

This function will indirectly be called for each preconditioner when cs_sles_finalize is called.

Parameters
[in]contextpointer to preconditioner context
[in]log_typelog type

◆ cs_sles_pc_setup_t

cs_sles_pc_setup_t

Function pointer for pre-resolution setup of a preconditioner context.

This setup may include building a multigrid hierarchy, for example.

Parameters
[in,out]contextpointer to solver context
[in]namepointer to name of linear system
[in]amatrix
[in]verbosityassociated verbosity

◆ cs_sles_pc_t

typedef struct _cs_sles_pc_t cs_sles_pc_t

◆ cs_sles_pc_tolerance_t

cs_sles_pc_tolerance_t

Function pointer for setting of the required tolerance for preconditioners involving an iterative solver.

This will usually not be relevant to non-iterative preconditioners, for which this type of function does not need to be defined.

The preconditioner is considered to have converged when residue/r_norm <= precision, residue being the L2 norm of a.vx-rhs.

Parameters
[in,out]contextpointer to solver context
[in]precisionsolver precision
[in]r_normresidue normalization

Enumeration Type Documentation

◆ cs_sles_pc_state_t

enum cs_sles_pc_state_t

Convergence status indicator.

Enumerator
CS_SLES_PC_DIVERGED 

The preconditioner has diverged

CS_SLES_PC_BREAKDOWN 

The preconditioner has broken down, and cannot make any more progress

CS_SLES_PC_MAX_ITERATION 

Maximum number of iterations has been reached, without reaching convergence

CS_SLES_PC_CONVERGED 

Function Documentation

◆ cs_sles_pc_apply()

cs_sles_pc_state_t cs_sles_pc_apply ( cs_sles_pc_t *  pc,
cs_halo_rotation_t  rotation_mode,
cs_real_t *  x_in,
cs_real_t *  x_out 
)

Apply a preconditioner.

If no options were previously provided for the matching system, default options will be used.

In cases where it is desired that the preconditioner modify a vector "in place", x_in should be set to NULL, and x_out contain the vector to be modified ( 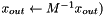$x_{out} \leftarrow M^{-1}x_{out})$).

Parameters
[in,out]pcpointer to preconditioner object
[in]rotation_modehalo update option for rotational periodicity
[in]x_ininput vector
[in,out]x_outinput/output vector
Returns
preconditioner application status

◆ cs_sles_pc_clone()

cs_sles_pc_t* cs_sles_pc_clone ( const cs_sles_pc_t *  src)

Create a new preconditioner context based on the copy of another.

The intended use of this function is to allow associating different preconditioners to related systems, so as to allow simultaneous setups and differentiate logging, while using the same settings by default.

If no preconditioner (i.e. NULL) is passed, it will return NULL.

Parameters
[in]srcpointer to source preconditioner object
Returns
pointer to new preconditioner object, or NULL

◆ cs_sles_pc_define()

cs_sles_pc_t* cs_sles_pc_define ( void *  context,
cs_sles_pc_get_type_t *  get_type_func,
cs_sles_pc_setup_t *  setup_func,
cs_sles_pc_tolerance_t *  tolerance_func,
cs_sles_pc_apply_t *  apply_func,
cs_sles_pc_free_t *  free_func,
cs_sles_pc_log_t *  log_func,
cs_sles_pc_clone_t *  clone_func,
cs_sles_pc_destroy_t *  destroy_func 
)

Define sparse linear equation preconditioner.

The context pointer is used to point to a structure adapted to the function pointers given here, and combined with those functions, allows using both built-in, external, or user-defined preconditioners.

Parameters
[in,out]contextpointer to preconditioner context structure (cs_sles_pc subsystem becomes owner)
[in]get_type_funcpointer to function returning type name
[in]setup_funcpointer to preconditioner setup function
[in]tolerance_funcpointer to tolerance setting functio
[in]apply_funcpointer to preconditioner application function (also calls setup_func if not done yet or free_func called since last apply)
[in]free_funcpointer function freeing system setup
[in]log_funcpointer to system info logging function (optional, but recommended)
[in]clone_funcpointer to settings clone function
[in]destroy_funcpointer to function destroying preconditioner context
Returns
pointer to associated preconditioner object

◆ cs_sles_pc_destroy()

void cs_sles_pc_destroy ( cs_sles_pc_t **  pc)

Destroy a sparse linear equation preconditioner.

Parameters
[in,out]pcpointer to preconditioner context structure

◆ cs_sles_pc_free()

void cs_sles_pc_free ( cs_sles_pc_t *  pc)

Free preconditioner setup.

This function frees resolution-related data, such as multigrid hierarchy, preconditioning, and any other temporary arrays or objects required for resolution, but maintains context information such as that used for logging (especially performance data).

Parameters
[in,out]pcpointer to preconditioner object

◆ cs_sles_pc_get_apply_func()

cs_sles_pc_apply_t* cs_sles_pc_get_apply_func ( const cs_sles_pc_t *  pc)

Return a pointer to the function used to apply a preconditioner.

This allows calling the preconditioner with one less level of indirection.

Parameters
[in]pcpointer to preconditioner object
Returns
preconditioner apply function

◆ cs_sles_pc_get_context()

void* cs_sles_pc_get_context ( cs_sles_pc_t *  pc)

Return pointer to preconditioner context structure pointer.

The context structure depends on the type of preconditioner used, which may in turn be determined by the string returned by cs_sles_pc_get_type(). If may be used by appropriate functions specific to that type.

Parameters
[in]pcpointer to preconditioner object
Returns
pointer to preconditioner-specific info and context

◆ cs_sles_pc_get_type()

const char* cs_sles_pc_get_type ( cs_sles_pc_t *  pc)

Return type name of preconditioner context.

The returned string is intended to help determine which type is associated with the void * pointer returned by cs_sles_pc_get_context for a given preconditioner definition, so as to be able to call additional specific functions beyond the generic functions assigned to a cs_sles_pc_t object.

Parameters
[in]pcpointer to preconditioner object
Returns
pointer to linear system preconditioner specific type name

◆ cs_sles_pc_get_type_name()

const char* cs_sles_pc_get_type_name ( cs_sles_pc_t *  pc)

Return type name of preconditioner context.

The returned string is intended mainly for logging.

Parameters
[in]pcpointer to preconditioner object

◆ cs_sles_pc_get_type_t()

const typedef char*() cs_sles_pc_get_type_t ( const void *  context,
bool  logging 
)

◆ cs_sles_pc_jacobi_create()

cs_sles_pc_t* cs_sles_pc_jacobi_create ( void  )

Create a Jacobi preconditioner.

Returns
pointer to newly created preconditioner object.

◆ cs_sles_pc_log()

void cs_sles_pc_log ( cs_sles_pc_t *  pc,
cs_log_t  log_type 
)

Log preconditioner setup, history and performance data.

This function frees resolution-related data, such as multigrid hierarchy, preconditioning, and any other temporary arrays or objects required for resolution, but maintains context information such as that used for logging (especially performance data).

Parameters
[in,out]pcpointer to preconditioner object
[in]log_typelog type

◆ cs_sles_pc_none_create()

cs_sles_pc_t* cs_sles_pc_none_create ( void  )

Create an "identity" (or null) preconditioner.

Returns
pointer to newly created preconditioner object.

◆ cs_sles_pc_poly_1_create()

cs_sles_pc_t* cs_sles_pc_poly_1_create ( void  )

Create a polynomial preconditioner of degree 1.

Returns
pointer to newly created preconditioner object.

Create a polynomial preconditioner of degree 1.

Returns
pointer to newly created preconditioner object.

◆ cs_sles_pc_poly_2_create()

cs_sles_pc_t* cs_sles_pc_poly_2_create ( void  )

Create a polynomial preconditioner of degree 2.

Returns
pointer to newly created preconditioner object.

Create a polynomial preconditioner of degree 2.

Returns
pointer to newly created preconditioner object.

◆ cs_sles_pc_set_tolerance()

void cs_sles_pc_set_tolerance ( cs_sles_pc_t *  pc,
double  precision,
double  r_norm 
)

Set the required tolerance for preconditioners involving an iterative solver.

This will usually not be relevant to non-iterative preconditioners, in which case this is a no-op.

If no options were previously provided for the matching system, default options will be used.

The system is considered to have converged when residue/r_norm <= precision, residue being the L2 norm of a.vx-rhs.

Parameters
[in,out]pcpointer to preconditioner object
[in]precisionpreconditioner precision
[in]r_normresidue normalization

◆ cs_sles_pc_setup()

void cs_sles_pc_setup ( cs_sles_pc_t *  pc,
const char *  name,
const cs_matrix_t *  a,
int  verbosity 
)

Setup sparse linear equation preconditioner.

Use of this function is optional: if a cs_sles_solve is called for the same system before this function is called, the latter will be called automatically.

If no options were previously provided for the matching system, default options will be used.

Parameters
[in,out]pcpointer to preconditioner object
[in]namelinear system name
[in]amatrix
[in]verbosityverbosity level
Generated on Thu Apr 9 2020 17:26:56 for My Project by   doxygen 1.8.16