|
My Project
programmer's documentation
|
|
My Project
programmer's documentation
|
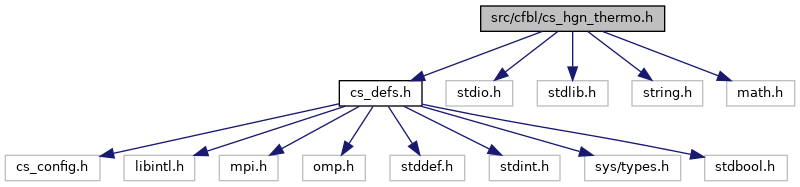
Go to the source code of this file.
Functions | |
| cs_real_t | cs_hgn_thermo_saturation_temp (cs_real_t pr) |
| Computation of the temperature at saturation with respect to the pressure. More... | |
| void | cs_hgn_thermo_pt (cs_real_t alpha, cs_real_t y, cs_real_t z, cs_real_t e, cs_real_t v, cs_real_t *ptp, cs_real_t *ppr) |
| Computation mixture pressure and temperature from volume, mass, energy fractions, as well as specific energy and specific volume. More... | |
| cs_real_t | cs_hgn_thermo_c2 (cs_real_t alpha, cs_real_t y, cs_real_t z, cs_real_t P, cs_real_t v) |
| Computation of the square of the sound speed in the mixture. More... | |
| cs_real_t | cs_hgn_thermo_ie (cs_real_t alpha, cs_real_t y, cs_real_t z, cs_real_t pr, cs_real_t v) |
Computation of the specific internal energy with respect to the volume ( 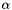 ), mass ( ), mass ( 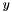 ) and energy ( ) and energy ( 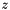 ) fractions, as well as the pressure and the specific volume ) fractions, as well as the pressure and the specific volume 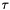 . More... . More... | |
| void | cs_hgn_thermo_eq (cs_real_t e, cs_real_t v, cs_real_t *palpha_eq, cs_real_t *py_eq, cs_real_t *pz_eq) |
| Computation of the equilibrium fractions. More... | |
Computation of the square of the sound speed in the mixture.
The sound speed may be computed through the Hessian matrices of the specific phasic entropies in the plane ( 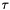 ,
, 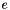 ).
). 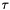 stands for specific volume, and
stands for specific volume, and 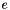 for specific energy. The sound speed is here estimated using the plane (
for specific energy. The sound speed is here estimated using the plane ( 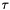 ,
, 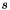 ).
). 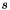 stands for specific entropy. We use the definition
stands for specific entropy. We use the definition
![\[ c^2 = -\tau^2 \der{P}{\tau}_{|s,y} \]](form_479.png)
. This relation is computed by a finite difference.
| [in] | alpha | volume fraction |
| [in] | y | mass fraction |
| [in] | z | energy fraction |
| [in] | P | pressure |
| [in] | v | specific volume |
| void cs_hgn_thermo_eq | ( | cs_real_t | e, |
| cs_real_t | v, | ||
| cs_real_t * | palpha_eq, | ||
| cs_real_t * | py_eq, | ||
| cs_real_t * | pz_eq | ||
| ) |
Computation of the equilibrium fractions.
The equilibrium fractions correspond to the definition of the mixture for which one gets the pressure, temperature and chemical potential equilibrium.
They are computed by using a Dichotomy algorithm on the function characterizing the equilibrium (two forms available).
The search for the equilibrium point is done in plane (P,T). Dichotomy is performed on the pressure along the saturation curve.
| [in] | e | specific internal energy |
| [in] | v | specific volume |
| [out] | palpha_eq | pointer to equilibrium volume fraction |
| [out] | py_eq | pointer to equilibrium mass fraction |
| [out] | pz_eq | pointer to equilibrium energy fraction |
Computation of the specific internal energy with respect to the volume ( 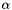 ), mass (
), mass ( 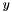 ) and energy (
) and energy ( 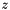 ) fractions, as well as the pressure and the specific volume
) fractions, as well as the pressure and the specific volume 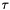 .
.
It uses a quasi-Newton method to solve:
![\[ \mathcal{P}(\alpha, y, z, e, \tau) = P \]](form_483.png)
| [in] | alpha | the volume fraction |
| [in] | y | the mass fraction |
| [in] | z | the energy fraction |
| [in] | pr | the pressure |
| [in] | v | the specific volume |
| void cs_hgn_thermo_pt | ( | cs_real_t | alpha, |
| cs_real_t | y, | ||
| cs_real_t | z, | ||
| cs_real_t | e, | ||
| cs_real_t | v, | ||
| cs_real_t * | ptp, | ||
| cs_real_t * | ppr | ||
| ) |
Computation mixture pressure and temperature from volume, mass, energy fractions, as well as specific energy and specific volume.
Following relations are used, that rely on phasic pressures and temperatures:
![\[ \dfrac{1}{T} = \dfrac{\dd s}{\dd e}_{|\tau,\alpha,y,z} \]](form_474.png)
![\[ \dfrac{P}{T} = \dfrac{\dd s}{\dd \tau}_{|e,\alpha,y,z} \]](form_475.png)
| [in] | alpha | volume fraction |
| [in] | y | mass fraction |
| [in] | z | energy fraction |
| [in] | e | specific energy |
| [in] | v | specific volume |
| [out] | ptp | pointer to mixture temperature |
| [out] | ppr | pointer to mixture pressure |
Computation of the temperature at saturation with respect to the pressure.
Compute the temperature at saturation 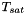 with respect to the pressure
with respect to the pressure 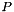 . It corresponds to the temperature for which the pressure, temperature and chemical potential are equal in both phases. It reduces to solve the equality of the phasic chemical potential:
. It corresponds to the temperature for which the pressure, temperature and chemical potential are equal in both phases. It reduces to solve the equality of the phasic chemical potential:
![\[ P \rightarrow T_{sat} \/ \mu_1(T_{sat},P)=\mu_2(T_{sat},P) \]](form_473.png)
This equality is solved using a Newton method.
| [in] | pr | pressure |
Compute the temperature at saturation 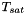 with respect to the pressure
with respect to the pressure 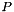 . It corresponds to the temperature for which the pressure, temperature and chemical potential are equal in both phases. It reduces to solve the equality of the phasic chemical potential:
. It corresponds to the temperature for which the pressure, temperature and chemical potential are equal in both phases. It reduces to solve the equality of the phasic chemical potential:
![\[ P \rightarrow T_{sat} \/ \mu_1(T_{sat},P)=\mu_2(T_{sat},P) \]](form_473.png)
This equality is solved using a secant method.
| [in] | pr | pressure |
 1.8.16
1.8.16