|
My Project
programmer's documentation
|
|
My Project
programmer's documentation
|
Return to equilibrium source terms computation for volume, mass, energy fractions in compressible homogeneous two-phase model. More...
#include "cs_config.h"#include "cs_defs.h"#include <stdio.h>#include <stdlib.h>#include <string.h>#include <math.h>#include <bft_mem.h>#include <bft_printf.h>#include "cs_math.h"#include "cs_mesh.h"#include "cs_field.h"#include "cs_field_pointer.h"#include "cs_hgn_thermo.h"#include "cs_prototypes.h"#include "cs_hgn_source_terms_step.h"
Functions | |
| void | cs_hgn_source_terms_step (const cs_mesh_t *m) |
| Compute the source terms for the two-phase flow model. More... | |
Return to equilibrium source terms computation for volume, mass, energy fractions in compressible homogeneous two-phase model.
A fractional step method used to solve the whole homogeneous two-phase. The last two steps solve the equations on the volume, mass, energy fractions:
1 ) a convection step perfomed by solving a pure convection equation on the volume, mass, energy fractions.
2 ) an update of these three fractions to account for the return to equilibrium source terms. This update is deduced by solving the ODE associated to the source term for each fraction.
Note that the energy, velocity and density remain constant throuh this fractional step but the pressure and the temperature depend on the fractions and thus evolve. They are updated at the end of the step using the thermodynamic relation defined in cs_hgn_thermo.c.
| void cs_hgn_source_terms_step | ( | const cs_mesh_t * | m | ) |
Compute the source terms for the two-phase flow model.
Update of these three fractions to account for the return to equilibrium source terms. This update is deduced by solving the ODE associated to the source term for each fraction.
First we compute the equilibrium fractions and second the fractions are relaxed towards those equilibrium values. Relaxation timescale 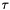 is to be provided by the user (equal to 1e-30 by default).
is to be provided by the user (equal to 1e-30 by default).
Note that the energy, velocity and density remain constant throuh this fractional step but the pressure and the temperature depend on the fractions and thus evolve. They are updated at the end of the step using the thermodynamic relation defined in cs_hg_thermo.c.
| [in] | m | pointer to mesh |
 1.8.16
1.8.16