|
My Project
programmer's documentation
|
•All Data Structures Namespaces Files Functions Variables Typedefs Enumerations Enumerator Macros Modules Pages
|
My Project
programmer's documentation
|
Symmetry boundary conditions for vectors and tensors. More...
Functions/Subroutines | |
| subroutine | clsyvt (nscal, icodcl, rcodcl, velipb, rijipb) |
| subroutine | clsyvt_scalar (iscal, icodcl) |
| subroutine | clsyvt_vector (iscal, icodcl) |
Symmetry boundary conditions for vectors and tensors.
Correspond to the code icodcl(ivar) = 4.
Please refer to the clsyvt section of the theory guide for more informations.
| subroutine clsyvt | ( | integer | nscal, |
| integer, dimension(:,:), pointer | icodcl, | ||
| double precision, dimension(:,:,:), pointer | rcodcl, | ||
| double precision, dimension(:,:) | velipb, | ||
| double precision, dimension(:,:), pointer | rijipb | ||
| ) |
| [in] | nscal | total number of scalars |
| [in,out] | icodcl | face boundary condition code:
|
| [in,out] | rcodcl | boundary condition values:
|
| [in] | velipb | value of the velocity at 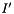 of boundary cells of boundary cells |
| [in] | rijipb | value of 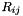 at at 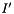 of boundary cells of boundary cells |
| subroutine clsyvt_scalar | ( | integer | iscal, |
| integer, dimension(nfabor,nvar) | icodcl | ||
| ) |
| [in] | iscal | scalar id |
| [in,out] | icodcl | face boundary condition code:
|
| subroutine clsyvt_vector | ( | integer | iscal, |
| integer, dimension(nfabor,nvar) | icodcl | ||
| ) |
| [in] | iscal | scalar id |
| [in,out] | icodcl | face boundary condition code:
|
 1.8.16
1.8.16