|
My Project
programmer's documentation
|
•All Data Structures Namespaces Files Functions Variables Typedefs Enumerations Enumerator Macros Modules Pages
|
My Project
programmer's documentation
|
Boundary conditions for smooth walls (icodcl = 5). More...
Functions/Subroutines | |
| subroutine | clptur (nscal, isvhb, icodcl, rcodcl, velipb, rijipb, visvdr, hbord, theipb) |
| subroutine | clptur_scalar (iscal, isvhb, icodcl, rcodcl, byplus, bdplus, buk, hbord, theipb, tetmax, tetmin, tplumx, tplumn) |
| subroutine | clptur_vector (iscal, isvhb, icodcl, rcodcl, byplus, bdplus, buk) |
Boundary conditions for smooth walls (icodcl = 5).
The wall functions may change the value of the diffusive flux.
The values at a boundary face 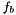 stored in the face center
stored in the face center 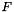 of the variable
of the variable 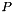 and its diffusive flux
and its diffusive flux 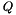 are written as:
are written as:
![\[ P_\centf = A_P^g + B_P^g P_\centi \]](form_72.png)
and
![\[ Q_\centf = A_P^f + B_P^f P_\centi \]](form_73.png)
where 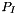 is the value of the variable
is the value of the variable 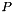 at the neighboring cell.
at the neighboring cell.
Warning:
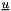 the boundary conditions may read:
the boundary conditions may read:
![\[ \vect{u}_\centf = \vect{A}_u^g + \tens{B}_u^g \vect{u}_\centi \]](form_76.png)
![\[ \vect{Q}_\centf = \vect{A}_u^f + \tens{B}_u^f \vect{u}_\centi \]](form_77.png)
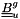 and
and 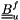 are 3x3 tensor matrix which coupled veclocity components next to a boundary.
are 3x3 tensor matrix which coupled veclocity components next to a boundary.Please refer to the wall boundary conditions section of the theory guide for more informations, as well as the clptur section.
| subroutine clptur | ( | integer | nscal, |
| integer | isvhb, | ||
| integer, dimension(:,:), pointer | icodcl, | ||
| double precision, dimension(:,:,:), pointer | rcodcl, | ||
| double precision, dimension(:,:) | velipb, | ||
| double precision, dimension(:,:), pointer | rijipb, | ||
| double precision, dimension(:), pointer | visvdr, | ||
| double precision, dimension(:), pointer | hbord, | ||
| double precision, dimension(:), pointer | theipb | ||
| ) |
| [in] | nscal | total number of scalars |
| [in] | isvhb | indicator to save exchange coeffient |
| [in,out] | icodcl | face boundary condition code:
|
| [in,out] | rcodcl | boundary condition values:
|
| [in] | velipb | value of the velocity at 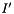 of boundary cells of boundary cells |
| [in] | rijipb | value of 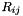 at at 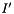 of boundary cells of boundary cells |
| [out] | visvdr | dynamic viscosity after V. Driest damping in boundary cells |
| [out] | hbord | exchange coefficient at boundary |
| [in] | theipb | value of thermal scalar at 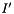 of boundary cells of boundary cells |
| subroutine clptur_scalar | ( | integer | iscal, |
| integer | isvhb, | ||
| integer, dimension(:,:), pointer | icodcl, | ||
| double precision, dimension(:,:,:), pointer | rcodcl, | ||
| double precision, dimension(:) | byplus, | ||
| double precision, dimension(:) | bdplus, | ||
| double precision, dimension(:) | buk, | ||
| double precision, dimension(:), pointer | hbord, | ||
| double precision, dimension(:), pointer | theipb, | ||
| double precision | tetmax, | ||
| double precision | tetmin, | ||
| double precision | tplumx, | ||
| double precision | tplumn | ||
| ) |
| [in] | iscal | scalar id |
| [in] | isvhb | indicator to save exchange coeffient |
| [in,out] | icodcl | face boundary condition code:
|
| [in,out] | rcodcl | boundary condition values:
|
| [in] | byplus | dimensionless distance to the wall |
| [in] | bdplus | dimensionless shift to the wall for scalable wall functions |
| [in] | buk | dimensionless velocity |
| [in,out] | hbord | exchange coefficient at boundary |
| [in] | theipb | value of thermal scalar at 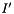 of boundary cells of boundary cells |
| [out] | tetmax | maximum local ustar value |
| [out] | tetmin | minimum local ustar value |
| [out] | tplumx | maximum local tplus value |
| [out] | tplumn | minimum local tplus value |
| subroutine clptur_vector | ( | integer | iscal, |
| integer | isvhb, | ||
| integer, dimension(:,:), pointer | icodcl, | ||
| double precision, dimension(:,:,:), pointer | rcodcl, | ||
| double precision, dimension(:) | byplus, | ||
| double precision, dimension(:) | bdplus, | ||
| double precision, dimension(:) | buk | ||
| ) |
| [in] | iscal | scalar id |
| [in] | isvhb | indicator to save exchange coeffient |
| [in,out] | icodcl | face boundary condition code:
|
| [in,out] | rcodcl | boundary condition values:
|
| [in] | byplus | dimensionless distance to the wall |
| [in] | bdplus | dimensionless shift to the wall for scalable wall functions |
| [in] | buk | dimensionless velocity |
| [in,out] | hbord | exchange coefficient at boundary |
 1.8.16
1.8.16