Local variables to be added
The following local variables need to be defined for the examples in this section:
integer ifac, iel, ii, ivar
integer izone
integer ilelt, nlelt
double precision uref2, d2s3
double precision rhomoy, xdh, xustar2
double precision xitur
double precision xkent, xeent
integer, allocatable, dimension(:) :: lstelt
double precision, dimension(:), pointer :: boundary_roughness
Initialization and finalization
The following initialization block needs to be added for the following examples:
allocate(lstelt(nfabor))
call field_get_val_s(ibrom, bfpro_rom)
Ad the end of the subroutine, it is recommended to deallocate the work array:
In theory Fortran 95 deallocates locally-allocated arrays automatically, but deallocating arrays in a symmetric manner to their allocation is good practice, and it avoids using a different logic for C and Fortran.
Body
In the body, we may define several boundary conditions. Here are a few examples.
Inlet example with hydraulic diameter
Assign an inlet to boundary faces of group '2' and x < 0.01.
- Warning
- the <, <=, >, and >= operators may only be used with variables x, y, and z. This syntax is not a full equation interpreter, so formulas involving x, y, or z are not allowed.
Set a a Dirichlet value on the three components of 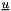 on the faces with the selection criterion '2 and x < 0.01' and set a Dirichlet to all the scalars
on the faces with the selection criterion '2 and x < 0.01' and set a Dirichlet to all the scalars 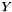 .
.
Turbulence example computed using equations valid for a pipe.
We will be careful to specify a hydraulic diameter adapted to the current inlet.
We will also be careful if necessary to use a more precise formula for the dynamic viscosity use in the calculation of the Reynolds number (especially if it is variable, it may be useful to take the law from usphyv. Here, we use by default the 'viscl0" value.
Regarding the density, we have access to its value at boundary faces (romb) so this value is the one used here (specifically, it is consistent with the processing in usphyv, in case of variable density).
call getfbr(
'2 and x < 0.01', nlelt, lstelt)
do ilelt = 1, nlelt
ifac = lstelt(ilelt)
iel = ifabor(ifac)
itypfb(ifac) = ientre
rcodcl(ifac,iu,1) = 1.1d0
rcodcl(ifac,iv,1) = 1.1d0
rcodcl(ifac,iw,1) = 1.1d0
uref2 = rcodcl(ifac,iu,1)**2 &
+ rcodcl(ifac,iv,1)**2 &
+ rcodcl(ifac,iw,1)**2
uref2 = max(uref2,1.d-12)
xdh = notebook_parameter_value_by_name('hydraulic_diam')
rhomoy = bfpro_rom(ifac)
call turbulence_bc_inlet_hyd_diam(ifac, uref2, xdh, rhomoy, viscl0, &
rcodcl)
if (nscal.gt.0) then
do ii = 1, nscal
rcodcl(ifac,isca(ii),1) = 1.d0
enddo
endif
enddo
Inlet example with turbulence intensity
Assign an inlet to boundary faces of group '3'.
Set a a Dirichlet value on the three components of 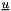 on the faces with the selection criterion '3' and set a Dirichlet to all the scalars
on the faces with the selection criterion '3' and set a Dirichlet to all the scalars 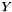 .
.
Turbulence example computed using turbulence intensity data.
We will be careful to specify a hydraulic diameter adapted to the current inlet.
Calculation of 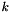 and
and 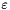 at the inlet (xkent and xeent) using the turbulence intensity and standard laws for a circular pipe (their initialization is not needed here but is good practice)
at the inlet (xkent and xeent) using the turbulence intensity and standard laws for a circular pipe (their initialization is not needed here but is good practice)
call getfbr(
'3', nlelt, lstelt)
do ilelt = 1, nlelt
ifac = lstelt(ilelt)
iel = ifabor(ifac)
itypfb(ifac) = ientre
rcodcl(ifac,iu,1) = 1.1d0
rcodcl(ifac,iv,1) = 1.1d0
rcodcl(ifac,iw,1) = 1.1d0
uref2 = rcodcl(ifac,iu,1)**2 &
+ rcodcl(ifac,iv,1)**2 &
+ rcodcl(ifac,iw,1)**2
uref2 = max(uref2,1.d-12)
xdh = notebook_parameter_value_by_name('hydraulic_diam')
xitur = notebook_parameter_value_by_name('turb_intensity')
call turbulence_bc_inlet_turb_intensity(ifac, uref2, xitur, xdh, &
rcodcl)
if (nscal.gt.0) then
do ii = 1, nscal
rcodcl(ifac,isca(ii),1) = 1.d0
enddo
endif
enddo
Assign an outlet to boundary faces of group 'outlet'
Outlet:
- zero flux for velocity and temperature, prescribed pressure
- Note that the pressure will be set to P0 at the first
- free outlet face (isolib)
call getfbr(
'outlet', nlelt, lstelt)
do ilelt = 1, nlelt
ifac = lstelt(ilelt)
itypfb(ifac) = isolib
enddo
Wall example
Assign a wall to boundary faces of group '5'.
Wall:
- zero flow (zero flux for pressure)
- friction for velocities (+ turbulent variables)
- zero flux for scalars
call getfbr(
'5', nlelt, lstelt)
do ilelt = 1, nlelt
ifac = lstelt(ilelt)
itypfb(ifac) = iparoi
if (nscal.gt.0) then
ii = 1
icodcl(ifac, isca(ii)) = 5
rcodcl(ifac, isca(ii), 1) = 20.d0
ii = 2
icodcl(ifac, isca(ii)) = 1
rcodcl(ifac, isca(ii),1) = 50.d0
rcodcl(ifac, isca(ii), 2) = 8.d0
ii = 3
icodcl(ifac, isca(ii)) = 3
rcodcl(ifac, isca(ii), 3) = 4.d0
endif
enddo
Rough wall example
Assign a rough wall to boundary faces of group '7'.
Wall:
- zero flow (zero flux for pressure)
- rough friction for velocities (+ turbulent variables)
- zero flux for scalars
call getfbr(
'7', nlelt, lstelt)
do ilelt = 1, nlelt
ifac = lstelt(ilelt)
itypfb(ifac) = iparug
rcodcl(ifac,iu,3) = 0.01d0
rcodcl(ifac,iv,3) = 0.01d0
rcodcl(ifac, iu, 1) = 1.d0
if (nscal.gt.0) then
ii = 1
icodcl(ifac, isca(ii)) = 6
rcodcl(ifac, isca(ii), 1) = 20.d0
ii = 3
icodcl(ifac, isca(ii)) = 3
rcodcl(ifac, isca(ii), 3) = 4.d0
endif
enddo
Symmetry example
Assign a symmetry condition to boundary faces of group '4'
call getfbr(
'4', nlelt, lstelt)
do ilelt = 1, nlelt
ifac = lstelt(ilelt)
itypfb(ifac) = isymet
enddo
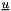 on the faces with the selection criterion '2 and x < 0.01' and set a Dirichlet to all the scalars
on the faces with the selection criterion '2 and x < 0.01' and set a Dirichlet to all the scalars 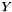 .
.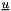 on the faces with the selection criterion '3' and set a Dirichlet to all the scalars
on the faces with the selection criterion '3' and set a Dirichlet to all the scalars 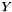 .
.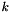 and
and 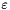 at the inlet (xkent and xeent) using the turbulence intensity and standard laws for a circular pipe (their initialization is not needed here but is good practice)
at the inlet (xkent and xeent) using the turbulence intensity and standard laws for a circular pipe (their initialization is not needed here but is good practice) 1.8.16
1.8.16