But templates allow us to do more than that. If not for compiler implementation limitations, templates could be used to program, at compile-time, just about anything we use computers for. This remarkable feat, offered by no other current-day computer language, stems from the fact that templates allow us to do three things at compile-time:
Of course, asking the compiler to compute, e.g., prime numbers, is one thing. But it's a completely different thing to do so in an award winning way. Don't expect speed records to be broken when the compiler performs complex calculations for us. But that's all beside the point. In the end we can ask the compiler to compute virtually anything using C++'s template language, including prime numbers....
In this chapter these remarkable features of templates are discussed. Following a short overview of subtleties related to templates the main characteristics of template meta programming are introduced.
In addition to template type and template non-type parameters there is a third kind of template parameter, the template template parameter. This kind of template parameter is introduced shortly, laying the groundwork for the discussion of trait classes and policy classes.
This chapter ends with the discussion of several additional and interesting applications of templates: adapting compiler error messages, conversions to class types and an elaborate example discussing compile-time list processing.
Much of the inspiration for this chapter came from two highly recommended books: Andrei Alexandrescu's 2001 book Modern C++ design (Addison-Wesley) and Nicolai Josutis and David Vandevoorde's 2003 book Templates (Addison-Wesley).
typename
was discussed. There we learned that it is not only used to define a name for
a (complex) type, but also to distinguish types defined by class templates
from members defined by class templates. In this section two more
applications of typename are introduced:
typename to situations
where types nested in templates are returned from member functions of class
templates;
typename section
23.1.3 introduces some new syntax that is related to the extended use of
the keyword typename: ::template, .template and ->template are
used to inform the compiler that a name used inside a template is itself a
class template.
nested returns an object of this nested class. The example uses a
(deprecated) in-class member implementation. The reason for this shortly
becomes clear.
template <typename T>
class Outer
{
public:
class Nested
{};
Nested nested() const
{
return Nested{};
}
};
The above example compiles flawlessly. Inside the class Outer there is
no ambiguity with respect to the meaning of nested's return type.
However, following good practices inline and template members should be implemented below their class interfaces (see section 7.8.1). So we remove the implementation from the interface and put it below the interface:
template <typename T>
class Outer
{
public:
class Nested
{};
Nested nested() const;
};
template <typename T>
Outer<T>::Nested Outer<T>::nested() const
{
return Nested{};
}
Suddenly the compiler refuses to compile the nested member. Fortunately,
it also suggests a solution in its error message:
error: need `typename' before `Outer<T>::Nested' because
`Outer<T>' is a dependent scope
Outer<T>::Nested Outer<T>::nested() const
~~~~~~~~
Now that the implementation has been moved out of the interface the return
type (i.e., Outer<T>::Nested) refers to a type defined by Outer<T>
rather than to a member of Outer<T>, and so typename must once again
be used.
A general rule for using typename can be formulated: the keyword
typename must be used whenever a type is referred to that is a subtype
of a type that itself depends on a template type parameter.
When using the inline implementation no such dependency is used as the
function's return type is simply Nested. When implementing the function
outside of the class interface (which should be considered `good practice')
then a specification of the class defining Nested must be provided for the
function's return type. So it becomes Outer<T>::Nested which clearly is a
type depending on a template type parameter.
Like before, writing typename in front of Outer<T>::Nested removes
the compilation error. Thus, the correct implementation of the function
nested becomes:
template <typename T>
typename Outer<T>::Nested Outer<T>::nested() const
{
return Nested();
}
Base and Derived, Base being
Derived's base class:
#include <iostream>
template <typename T>
class Base
{
public:
void member();
};
template <typename T>
void Base<T>::member()
{
std::cout << "This is Base<T>::member()\n";
}
template <typename T>
class Derived: public Base<T>
{
public:
Derived();
};
template <typename T>
Derived<T>::Derived()
{
member();
}
This example won't compile, and the compiler tells us something like:
error: there are no arguments to 'member' that depend on a template
parameter, so a declaration of 'member' must be available
This error causes some confusion as ordinary (non-template) base classes
readily make their public and protected members available to classes that are
derived from them. This is no different for class templates, but only if the
compiler can figure out what we mean. In the above example the compiler
can't as it doesn't know for what type T the member function
member must be initialized when called from Derived<T>::Derived.
To appreciate why this is true, consider the situation where we have defined a specialization:
template <>
Base<int>::member()
{
std::cout << "This is the int-specialization\n";
}
Since the compiler, when Derived<SomeType>::Derived is called, does
not know whether a specialization of member is in effect, it can't
decide (when compiling Derived<T>::Derived) for what type to instantiate
member. It can't decide this when compiling Derived<T>::Derived as
member's call in Derived::Derived doesn't require a template type
parameter.
In cases like these, where no template type parameter is available to
determine which type to use, the compiler must be told that it should postpone
its decision about the template type parameter to use (and therefore about the
particular (here: member) function to call)
until instantiation time.
This may be implemented in two ways: either by using this or by
explicitly mentioning the base class, instantiated for the derived class's
template type(s). When this is used the compiler is informed that we're
referring to the type T for which the template was instantiated. Any
confusion about which member function to use (the derived class or base class
member) is resolved in favor of the derived class member. Alternatively, the
base or derived class can explicitly be mentioned (using Base<T> or
Derived<T>) as shown in the next example. Note that with the int
template type the int specialization is used.
#include <iostream>
template <typename T>
class Base
{
public:
void member();
};
template <typename T>
void Base<T>::member()
{
std::cout << "This is Base<T>::member()\n";
}
template <>
void Base<int>::member()
{
std::cout << "This is the int-specialization\n";
}
template <typename T>
class Derived: public Base<T>
{
public:
Derived();
virtual void member();
};
template <typename T>
void Derived<T>::member()
{
std::cout << "This is Derived<T>::member()\n";
}
template <typename T>
Derived<T>::Derived()
{
this->member(); // Using `this' implies using the
// type for which T was instantiated
Derived<T>::member(); // Same: calls the Derived member
Base<T>::member(); // Same: calls the Base member
std::cout << "Derived<T>::Derived() completed\n";
}
int main()
{
Derived<double> d;
Derived<int> i;
}
/*
Generated output:
This is Derived<T>::member()
This is Derived<T>::member()
This is Base<T>::member()
Derived<T>::Derived() completed
This is Derived<T>::member()
This is Derived<T>::member()
This is the int-specialization
Derived<T>::Derived() completed
*/
The above example also illustrates the use of virtual member templates
(although virtual member templates aren't often used). In the example Base
declares a virtual void member and Derived defines its overriding
function member. In that case this->member() in Derived::Derived
calls, due to member's virtual nature, Derived::member. The statement
Base<T>::member(), however, always calls Base's member function
and can be used to
bypass dynamic polymorphism.
typename keyword may often be used for that purpose.
But typename cannot always come to the rescue. While parsing a source the
compiler receives a series of tokens, representing meaningful units of
text encountered in the program's source. A token could represent, e.g., an
identifier or a number. Other tokens represent operators, like =, + or
<. It is precisely the last token that may cause problems as it may have
very different meanings. The correct meaning cannot always be determined from
the context in which the compiler encounters <. In some situations the
compiler does know that < does not represent the less than
operator, as when a template parameter list follows the keyword template,
e.g.,
template <typename T, int N>
Clearly, in this case < does not represent a `less than' operator.
The special meaning of < when it is preceded by template forms the
basis for the syntactic constructs discussed in this section.
Assume the following class has been defined:
template <typename Type>
class Outer
{
public:
template <typename InType>
class Inner
{
public:
template <typename X>
void nested();
};
};
The class template Outer defines a nested class template
Inner. Inner in turn defines a template member function.
Next a class template Usage is defined, offering a member function
caller expecting an object of the above Inner type. An initial setup
for Usage looks like this:
template <typename T1, typename T2>
class Usage
{
public:
void caller(Outer<T1>::Inner<T2> &obj);
...
};
The compiler won't accept this as it interprets Outer<T1>::Inner as a
class type. But there is no class Outer<T1>::Inner. Here the compiler
generates an error like:
error: 'class Outer<T1>::Inner' is not a type
To inform the compiler that Inner
itself is a template, using the template type parameter <T2>, the
::template construction is required. It tells the compiler that the next
< should not be interpreted as a `less than' token, but rather as a
template type argument. So, the declaration is modified to:
void caller(Outer<T1>::template Inner<T2> &obj);
This still doesn't get us where we want to be: after all Inner<T2> is
a type, nested under a class template, depending on a template type
parameter. In fact, the original Outer<T1>::Inner<T2> &obj declaration
results in a series of error messages, one of them looking like this:
error: expected type-name before '&' token
As is often the case this error message nicely indicates what should be
done to get it right: add typename:
void caller(typename Outer<T1>::template Inner<T2> &obj);
Of course, caller itself is not only just declared, it must also be
implemented. Assume that its implementation should call Inner's member
nested, instantiated for yet another type X. The class template
Usage should therefore receive a third template type parameter, called
T3. Assume it has been defined. To implement caller, we write:
void caller(typename Outer<T1>::template Inner<T2> &obj)
{
obj.nested<T3>();
}
Once again we run into a problem. In the function's body the compiler once
again interprets < as `less than', seeing a logical expression having as
its right-hand side a primary expression instead of a function call specifying
a template type T3.
To tell the compiler that is should interpret <T3> as a type to
instantiate, the template keyword must once again be used. This
time it is used in the context of the member selection operator. We write
.template to inform the compiler that what follows is not a `less than'
operator, but rather a type specification. The function's final implementation
becomes:
void caller(typename Outer<T1>::template Inner<T2> &obj)
{
obj.template nested<T3>();
}
Instead of defining value or reference parameters functions may also
define pointer parameters. Had obj been defined as a pointer parameter the
implementation would have had to use the ->template construction, rather
than the .template construction. E.g.,
void caller(typename Outer<T1>::template Inner<T2> *ptr)
{
ptr->template nested<T3>();
}
As we've seen class templates can be derived from base class templates. The base class template can declare a static member template, which is available to a class that is derived from this base class. Such a base class might look like this:
template <typename Type>
struct Base
{
template <typename Tp>
static void fun();
};
Normally, when a base class defines a static member we can just call that member by prefixing its name by its class name. E.g.,
int main()
{
Base<int>::fun<double>();
}
This also works fine if a class Derived is derived from Base,
instantiated for a specific type:
struct Der: public Base<int>
{
static void call()
{
Base<int>::fun<int>(); // OK
fun<int>(); // also OK
};
};
However, when the derived class itself is a class template this way to
call fun does not compile anymore, as it interprets Base<Type>::fun in
Base<Type>::fun<int> as a type, to be instantiated for int. This
interpretation can be overruled by us by indicating that fun itself is a
template. For this the ::template prefix is used:
template <typename Type>
struct Der: public Base<Type>
{
//template <typename Tp> // 'call' may be a member template
//static // 'call' may be a static member
void call()
{
// fun<int>(); // won't compile
// Base<Type>::fun<int>(); // won't compile
Base<Type>::template fun<int>(); // OK
Base<Type>::template fun<Tp>(); // OK if call is a
// member template
};
};
enum
values. Enums are preferred over, e.g., int const values since enums never
require any linkage. They are pure symbolic values with no memory
representation whatsoever.
Consider the situation where a programmer must use a cast, say a
reinterpret_cast. A problem with a reinterpret_cast is that it is the
ultimate way to turn off all compiler checks. All bets are off, and we can
write extreme but absolutely pointless reinterpret_cast statements, like
int intVar = 12;
ostream &ostr = reinterpret_cast<ostream &>(intVar);
Wouldn't it be nice if the compiler would warn us against such oddities by generating an error message?
If that's what we'd like the compiler to do, there must be some way to
distinguish madness from weirdness. Let's assume we agree on the following
distinction: reinterpret casts are never acceptable if the target type
represents a larger type than the expression (source) type, since that would
immediately result in exceeding the amount of memory that's actually available
to the target type. For this reason it's clearly silly to
reinterpret_cast<double *>(&intVar), but reinterpret_cast<char
*>(&intVar) could be defensible.
The intent is now to create a new kind of cast, let's call it
reinterpret_to_smaller_cast. It should only be allowed to perform a
reinterpret_to_smaller_cast if the target type occupies less memory than
the source type (note that this exactly the opposite reasoning as used by
Alexandrescu (2001), section 2.1).
To start, we construct the following template:
template<typename Target, typename Source>
Target &reinterpret_to_smaller_cast(Source &source)
{
// determine whether Target is smaller than source
return reinterpret_cast<Target &>(source);
}
At the comment an enum-definition is inserted defining a symbol having a
suggestive name. A compile-time error results if the required condition is
not met and the error message displays the name of the symbol. A division by
zero is clearly not allowed, and noting that a false value represents a
zero value, the condition could be:
1 / (sizeof(Target) <= sizeof(Source));
The interesting part is that this condition doesn't result in any code at all. The enum's value is a plain value that's computed by the compiler while evaluating the expression:
template<typename Target, typename Source>
Target &reinterpret_to_smaller_cast(Source &source)
{
enum
{
the_Target_size_exceeds_the_Source_size =
1 / (sizeof(Target) <= sizeof(Source))
};
return reinterpret_cast<Target &>(source);
}
When reinterpret_to_smaller_cast is used to cast from int to
double an error is produced by the compiler, like this:
error: enumerator value for 'the_Target_size_exceeds_the_Source_size'
is not an integer constant
whereas no error is reported if, e.g.,
reinterpret_to_smaller_cast<int>(doubleVar) is requested with
doubleVar defined as a double.
In the above example an enum was used to compute (at compile-time) a
value that is illegal if an assumption is not met. The creative part is
finding an appropriate expression.
Enum values are well suited for these situations as they do not consume any memory and their evaluation does not produce any executable code. They can be used to accumulate values too: the resulting enum value then contains a final value, computed by the compiler rather than by executable code as the next sections illustrate. In general, programs shouldn't do run-time what they can do at compile-time and performing complex calculations resulting in constant values is a clear example of this principle.
int values. This is useful in situations where a scalar value (often a
bool value) is available to select a specialization but a type is required
to base the selection on. This situation is shortly encountered (section
23.2.2).
Templatizing
integral values is based on the fact that a
class template together with its template arguments defines a type. E.g.,
vector<int> and vector<double> are different types.
Turning integral values into templates is easily done. Define a template (it
does not have to have any content at all) and store the integral value in an
enum:
template <int x>
struct IntType
{
enum { value = x };
};
As IntType does not have any members the `class IntType' can be
defined as `struct IntType', saving us from having to type public:.
Defining the enum value `value' allows us to retrieve the value
used at the instantiation at no cost in storage. Enum values are neither
variables nor data members and thus have no address. They are mere values.
It's easy to use the struct IntType. An anonymous or named
object can be defined by specifying a value for its int non-type
parameter. Example:
int main()
{
IntType<1> it;
cout << "IntType<1> objects have value: " << it.value << "\n" <<
"IntType<2> objects are of a different type "
"and have values " << IntType<2>().value << '\n';
}
Actually, neither the named object nor the anonymous object is
required. As the enum is defined as a plain value, associated with the
struct IntType we merely have to specify the specific int for which
the struct IntType is defined to retrieve its `value', like this:
int main()
{
cout << "IntType<100>, no object, defines `value': " <<
IntType<100>::value << "\n";
}
if and
switch statements. If we want to be able to `program the compiler'
this feature must also be offered by templates.
Like templates storing values templates making choices do not require any code to be executed at run-time. The selection is purely made by the compiler, at compile-time. The essence of template meta programming is that we are not using or relying on any executable code. The result of a template meta program often is executable code, but that code is a function of decisions merely made by the compiler.
Template (member) functions are only instantiated when they are actually used. Consequently we can define specializations of functions that are mutually exclusive. Thus it is possible to define a specialization that can be compiled in situation one, but not in situation two and to define another specialization that can be compiled in situation two, but not in situation one. Using specializations code can be generated that is tailored to the demands of a particular situation.
A feature like this cannot be implemented in run-time executable code. For example, when designing a generic storage class the software engineer may intend to store value class type objects as well as objects of polymorphic class types in the final storage class. Thus the software engineer may conclude that the storage class should contain pointers to objects, rather than the objects themselves. The initial implementation attempt could look like this:
template <typename Type>
void Storage::add(Type const &obj)
{
d_data.push_back(
d_ispolymorphic ?
obj.clone()
:
new Type{obj}
);
}
The intent is to use the clone member function of the class Type
if Type is a polymorphic class and the standard copy constructor if
Type is a value class.
Unfortunately, this scheme usually fails as value classes do not define
clone member functions and polymorphic base classes should delete
their copy constructors (cf. section 7.6). It doesn't matter to the
compiler that clone is never called for value classes and that the copy
constructor is only available in value classes and not in polymorphic
classes. It merely has some code to compile, and can't do that because of
missing members. It's as simple as that.
add member functions of which only one is going to be called
(and thus instantiated). Our selection will be based on an additional (in
addition to Type itself) template non-type parameter that indicates
whether we'll use Storage for polymorphic or non-polymorphic classes. Our
class Storage starts like this:
template <typename Type, bool isPolymorphic>
class Storage
Initially two overloaded versions of our add member are defined:
one used with Storage objects storing polymorphic objects (using true
as its template non-type argument) and one storing value
class objects (using false as its template non-type argument).
Unfortunately we run into a small problem: functions cannot be overloaded
by their argument values but only by their argument types. But the
small problem may be solved. Realizing that types are defined by the
combination of template names and their template arguments we may convert the
values true and false into types using the knowledge from section
23.2.1.1 about how to convert integral values to types.
We'll provide one (private) add member with an IntType<true> parameter
(implementing the polymorphic class) and another (private) add member with
an IntType<false> parameter (implementing the non-polymorphic class).
In addition to these two private members a third (public) member add is
defined calling the appropriate private add member by providing an
IntType argument, constructed from Storage's template non-type
parameter.
Here are the implementations of the three add members:
// declared in Storage's private section:
template <typename Type, bool isPolymorphic>
void Storage<Type, isPolymorphic>::add(Type const &obj, IntType<true>)
{
d_data.push_back(obj.clone());
}
template <typename Type, bool isPolymorphic>
void Storage<Type, isPolymorphic>::add(Type const &obj, IntType<false>)
{
d_data.push_back(new Type(obj));
}
// declared in Storage's public section:
template <typename Type, bool isPolymorphic>
void Storage<Type, isPolymorphic>::add(Type const &obj)
{
add(obj, IntType<isPolymorphic>());
}
The appropriate add member is instantiated and called because a
primitive value can be converted to a type. Each of the possible template
non-type values is thus used to define an overloaded class template member
function.
Since class template members are only instantiated when used only one of
the overloaded private add members is instantiated. Since the other one is
never called (and thus never instantiated) compilation errors are prevented.
Storage class that uses pointers to store copies of value class
objects. Their argument is that value class objects can very well be stored by
value, rather than by pointer. They'd rather store value class objects by
value and polymorphic class objects by pointer.
Such distinctions frequently occur in template meta programming and
the following struct IfElse
may be used to obtain one of two types, depending on a bool selector
value.
First define the generic form of the template:
template<bool selector, typename FirstType, typename SecondType>
struct IfElse
{
using type = FirstType;
};
Then define a partial specialization. The specialization represents
a specific selector value (e.g., false) and leaves the remaining types
open to further specification:
template<typename FirstType, typename SecondType>
struct IfElse<false, FirstType, SecondType>
{
using type = SecondType;
};
The former (generic) definition associates FirstType with the
IfElse::type type definition, the latter definition (partially specialized
for the logical value false) associates SecondType with the
IfElse::type type definition.
The IfElse template allows us to define class templates whose data
organization is conditional to the template's parameters.
Using IfElse the Storage class may define
pointers to store copies of polymorphic class type objects and values
to store value class type objects:
template <typename Type, bool isPolymorphic>
class Storage
{
using DataType = typename IfElse<isPolymorphic, Type *, Type>::type;
std::vector<DataType> d_data;
private:
void add(Type const &obj, IntType<true>);
void add(Type const &obj, IntType<false>);
public:
void add(Type const &obj);
}
template <typename Type, bool isPolymorphic>
void Storage<Type, isPolymorphic>::add(Type const &obj, IntType<true>)
{
d_data.push_back(obj.clone());
}
template <typename Type, bool isPolymorphic>
void Storage<Type, isPolymorphic>::add(Type const &obj, IntType<false>)
{
d_data.push_back(obj);
}
template <typename Type, bool isPolymorphic>
void Storage<Type, isPolymorphic>::add(Type const &obj)
{
add(obj, IntType<isPolymorphic>());
}
The above example uses IfElse's type, defined by IfElse as
either FirstType or SecondType. IfElse's type defines the
actual data type to use for Storage's vector data type.
The remarkable result in this example is that the data organization of
the Storage class now depends on its template arguments. Since the
isPolymorphic == true situation uses different data types than the
isPolymorphic == false situation, the overloaded private add members
can utilize this difference immediately. E.g., add(Type const &obj,
IntType<false>) uses direct copy construction to store a copy of obj
in d_vector.
It is also possible to make a selection from multiple types as IfElse
structs can be nested. Realize that using IfElse never has any effect on
the size or execution time of the final executable program. The final program
simply contains the appropriate type, conditional to the type that's
eventually selected.
MapType as a map having plain types or
pointers for either its key or value types, illustrates this approach:
template <typename Key, typename Value, int selector>
class Storage
{
using MapType =
typename IfElse<
selector == 1, // if selector == 1:
map<Key, Value>, // use map<Key, Value>
typename IfElse<
selector == 2, // if selector == 2:
map<Key, Value *>, // use map<Key, Value *>
typename IfElse<
selector == 3, // if selector == 3:
map<Key *, Value>, // use map<Key *, Value>
// otherwise:
map<Key *, Value *> // use map<Key *, Value *>
>::type
>::type
>::type;
MapType d_map;
public:
void add(Key const &key, Value const &value);
private:
void add(Key const &key, Value const &value, IntType<1>);
...
};
template <typename Key, typename Value, int selector>
inline void Storage<selector, Key, Value>::add(Key const &key,
Value const &value)
{
add(key, value, IntType<selector>());
}
The principle used in the above examples is: if class templates may use
data types that depend on template non-type parameters, an IfElse struct
can be used to select the appropriate data types. Knowledge about the various
data types may also be used to define overloaded member functions. The
implementations of these overloaded members may then be optimized to the
various data types. In programs only one of these alternate functions (the one
that is optimized to the actually used data types) will then be instantiated.
The private add functions define the same parameters as the public
add wrapper function, but add a specific IntType type, allowing the
compiler to select the appropriate overloaded version based on the template's
non-type selector parameter.
for or while statement. However, iterations
can always be rewritten as recursions. Recursions are supported
by templates and so iterations can always be implemented as (tail) recursions.
To implement iterations by (tail) recursion do as follows:
enum values.
Most readers are probably familiar with the recursive implementation of
the mathematical `factorial' operator, commonly represented by the
exclamation mark (!): n factorial (so: n!) returns the successive
products n * (n - 1) * (n - 2) * ... * 1, representing the number of ways
n objects can be permuted. Interestingly, the factorial operator is itself
usually defined by a recursive definition:
n! = (n == 0) ?
1
:
n * (n - 1)!
To compute n! from a template, a template Factorial can be defined
using an int n template non-type parameter. A specialization is defined
for the case n == 0. The generic implementation uses recursion according
to the factorial definition. Furthermore, the Factorial template defines
an enum value `value' containing its factorial value. Here is the
generic definition:
template <int n>
struct Factorial
{
enum { value = n * Factorial<n - 1>::value };
};
Note how the expression assigning a value to `value' uses constant
values that can be determined by the compiler. The value n is provided, and
Factorial<n - 1> is computed using template meta
programming. Factorial<n-1> in turn results in value that can be
determined by the compiler (viz.
Factorial<n-1>::value). Factorial<n-1>::value represents the value
defined by the type Factorial<n - 1>. It is not the value returned
by an object of that type. There are no objects here but merely values
defined by types.
The recursion ends in a specialization. The compiler selects the specialization (provided for the terminating value 0) instead of the generic implementation whenever possible. Here is the specialization's implementation:
template <>
struct Factorial<0>
{
enum { value = 1 };
};
The Factorial template can be used to determine, compile time, the
number of permutations of a fixed number of objects. E.g.,
int main()
{
cout << "The number of permutations of 5 objects = " <<
Factorial<5>::value << "\n";
}
Once again, Factorial<5>::value is not evaluated at run-time, but
at compile-time. The run-time equivalent of the above cout statement is,
therefore:
int main()
{
cout << "The number of permutations of 5 objects = " <<
120 << "\n";
}
template <char ...Chars>
Type operator "" _identifier()
This variadic non-type parameter function template defines no parameters, but merely a variadic non-type parameter list.
Its argument must be an int constant, as is also expected by the literal
operator defining an unsigned long long int parameter. All the characters
of the int constant are passed as individual char non-type template
arguments to the literal operator.
For example, if _NM2km is a literal operator function template, it can
be called as 80_NM2km. The function template is then actually called as
_NM2km<'8', '0'>(). If this function template merely uses template meta
programming techniques and only processes integral data then its actions can
be performed completely at compile-time. To illustrate this, let's assume
NM2km only processes and returns unsigned values.
The function template _NM2km can forward its argument to a class template,
defining an enum constant value, and that performs the required
computations. Here is the implementation of the variadic literal operator
function template _NM2km:
template <char ... Chars>
size_t constexpr operator "" _NM2km()
{
return static_cast<size_t>( // forward Chars to NM2km
NM2km<0, Chars ...>::value * 1.852);
}
The class template NM2km defines three non-type parameters: acc
accumulates the value, c is the first character of the variadic non-type
parameters, while ...Chars represents the remaining non-type parameters,
contained in a non-type parameter pack. Since c is, at each recursive
call, the next character from the original non-type parameter pack, the value
so far multiplied by 10 plus the value of the next character is passed as the
next accumulated value to its recursive call, together with the remaining
elements of the parameter pack, represented by Chars ...:
template <size_t acc, char c, char ...Chars>
struct NM2km
{
enum
{
value = NM2km<10 * acc + c - '0', Chars ...>::value
};
};
Eventually, the parameter pack is empty. For this case a partial
specialization of NM2km is available:
template <size_t acc, char c> // empty parameter pack
struct NM2km<acc, c>
{
enum
{
value = 10 * acc + c - '0'
};
};
This works fine, but of course not in cases where binary, octal, or
hexadecimal values must also be interpreted. In that case we must first
determine whether the first character(s) indicate a special number
system. This can be determined by the class template NM2kmBase, that is
now called from the _NM2km literal operator:
template <char ... Chars>
size_t constexpr operator "" _NM2km()
{
return static_cast<size_t>( // forward Chars to NM2kmBase
NM2kmBase<Chars ...>::value * 1.852);
}
The NM2kmBase class template normally assumes the decimal number
system, passing base value 10 and initial sum 0 to NM2km. The NM2km
class template is provided with an additional (first) non-type parameter
representing the base value of the number system to use. Here is
NM2kmBase:
template <char ...Chars>
struct NM2kmBase
{
enum
{
value = NM2km<10, 0, Chars ...>::value
};
};
Partial specializations handle the different number systems, by inspecting the first (one or two) characters:
template <char ...Chars>
struct NM2kmBase<'0', Chars ...> // "0..."
{
enum
{ // octal value: base 8
value = NM2km<8, 0, Chars ...>::value
};
};
template <char ...Chars>
struct NM2kmBase<'0', 'b', Chars ...> // "0b..."
{
enum
{ // binary value: base 2
value = NM2km<2, 0, Chars ...>::value
};
};
template <char ...Chars>
struct NM2kmBase<'0', 'x', Chars ...> // "0x..."
{
enum
{ // hex value: base 16
value = NM2km<16, 0, Chars ...>::value
};
};
NM2km is implemented as before, albeit that it can now handle
various number systems. The conversion from character to numeric value is left
to a small support function template, cVal:
template <char c>
int constexpr cVal()
{
return '0' <= c <= '9' ? c - '0' : 10 + c - 'a';
}
template <size_t base, size_t acc, char c, char ...Chars>
struct NM2km
{
enum
{
value = NM2km<base, base * acc + cVal<c>(),
Chars ...>::value
};
};
template <size_t base, size_t acc, char c>
struct NM2km<base, acc, c>
{
enum { value = base * acc + cVal<c>() };
};
Storage. Data stored in Storage objects may either make
and store copies of the data or store the data as received. Storage
objects may also either use a vector or a linked list as its underlying
storage medium. How should the engineer tackle this request? Should four
different Storage classes be designed?
The engineer's first reaction could be to develop an all-in Storage class.
It could have two data members, a list and a vector, and its constructor could
be provided with maybe an enum value indicating whether the data itself or new
copies should be stored. The enum value can be used to initialize a series of
pointers to member functions performing the requested tasks (e.g., using a
vector to store the data or a list to store copies).
Complex, but doable. Then the engineer is asked to modify the class: in the
case of new copies a custom-made allocation scheme should be used rather than
the standard new operator. He's also asked to allow the use of yet
another type of container, in addition to the vector and the list that were
already part of the design. Maybe a deque would be preferred or maybe even
a stack.
It's clear that the approach aiming at implementing all functionality and all
possible combinations in one class doesn't scale. The class Storage soon
becomes a monolithic giant which is hard to understand, maintain, test, and
deploy.
One of the reasons why the big, all-encompassing class is hard to deploy and understand is that a well-designed class should enforce constraints: the design of the class should, by itself, disallow certain operations, violations of which should be detected by the compiler, rather than by a program that might terminate in a fatal error.
Think about the above request. If the class offers both an interface to access
the vector data storage and an interface to access the list data storage,
then it's likely that the class offers an overloaded operator[] member
to access elements in the vector. This member, however, will be syntactically
present, but semantically invalid when the list data storage is selected,
which doesn't support operator[].
Sooner or later, users of the monolithic all-encompassing class
Storage will fall into the trap of using operator[] even though
they've selected the list as the underlying data storage. The compiler won't
be able to detect the error, which only appears once the program is
running, confusing its users.
The question remains: how should the engineer proceed, when confronted with the above questions? It's time to introduce policies.
In the previous section the problem of creating a class that might use any of a series of allocation schemes was introduced. These allocation schemes all depend on the actual data type to use, and so the `template reflex' should kick in.
Allocation schemes should probably be defined as template classes, applying
the appropriate allocation procedures to the data type at hand. When such
allocation schemes are used by the familiar STL containers (like
std::vector, std::stack, etc.), then such home-made allocation schemes
should probably be derived from std::allocator, to provide
for the requirements made by these containers. The class template
std::allocator is declared by the <memory> header file and the three
allocation schemes developed here were all derived from std::allocator.
Using in-class implementations for brevity the following allocation classes could be defined:
Data is used `as is':
template <typename Data>
class PlainAlloc: public std::allocator<Data>
{
template<typename IData>
friend std::ostream &operator<<(std::ostream &out,
PlainAlloc<IData> const &alloc);
Data d_data;
public:
PlainAlloc()
{}
PlainAlloc(Data const &data)
:
d_data(data)
{}
PlainAlloc(PlainAlloc<Data> const &other)
:
d_data(other.d_data)
{}
};
new operator to
allocate a new copy of the data:
template <typename Data>
class NewAlloc: public std::allocator<Data>
{
template<typename IData>
friend std::ostream &operator<<(std::ostream &out,
NewAlloc<IData> const &alloc);
Data *d_data;
public:
NewAlloc()
:
d_data(0)
{}
NewAlloc(Data const &data)
:
d_data(new Data(data))
{}
NewAlloc(NewAlloc<Data> const &other)
:
d_data(new Data(*other.d_data))
{}
~NewAlloc()
{
delete d_data;
}
};
request,
obtaining the required amount of memory, is left as an exercise to the
reader):
template<typename Data>
class PlacementAlloc: public std::allocator<Data>
{
template<typename IData>
friend std::ostream &operator<<(std::ostream &out,
PlacementAlloc<IData> const &alloc);
Data *d_data;
static char s_commonPool[];
static char *s_free;
public:
PlacementAlloc()
:
d_data(0)
{}
PlacementAlloc(Data const &data)
:
d_data(new(request()) Data(data))
{}
PlacementAlloc(PlacementAlloc<Data> const &other)
:
d_data(new(request()) Data(*other.d_data))
{}
~PlacementAlloc()
{
d_data->~Data();
}
private:
static char *request();
};
Storage introduced in the previous section. In addition
to these classes, additional allocation schemes could be implemented by the
user as well.
To apply the proper allocation scheme to the class Storage,
Storage should be designed as a class template itself. The class also
needs a template type parameter allowing users to specify the data type.
The data type to be used by a particular allocation scheme could of course
be specified when specifying the allocation scheme to use. The class
Storage would then have two template type parameters, one for the data
type, one for the allocation scheme:
template <typename Data, typename Scheme>
class Storage ...
To use the class Storage we would then write, e.g.:
Storage<string, NewAlloc<string>> storage;
Using Storage this way is fairly complex and potentially error-prone,
as it requires the user to specify the data type twice. Instead, the
allocation scheme should be specified using a new type of template parameter,
not requiring the user to specify the data type required by the allocation
scheme. This new kind of template parameter (in addition to the well-known
template type parameter and template non-type parameter) is called the
template template parameter.
Starting with the C++14 standard the keyword class
in the syntactical form of template template parameters (template
<parameter specifications> class Name) is no longer required. From that
standard onward, the keyword typename can also be used (e.g., template
<parameter specifications> typename Name).
To specify an allocation policy, rather than an allocation type
for the class Storage we rephrase its class template header:
definition starts as follows:
template <typename Data, template <typename> class Policy>
class Storage...
The second template parameter is new. It is a template template parameter. It has the following elements:
template, starting the template template parameter;
template is followed (between angle brackets) by a
list of template parameters that must be specified for the template
template parameter. These parameters may be given names, but names
are usually omitted as those names cannot be used in subsequent
template definitions. On the other hand, providing formal names may
help the reader of the template to understand the kind of templates
that must be specified with the template template parameter.
class or typename
must be specified.
template <
template <
typename = std::string,
int = 12,
template <typename = int> class Inner = std::vector
>
class Policy
>
class Demo
{
...
};
Here, the class template Demo expects a template template parameter
named Policy, expecting three template parameters: a template type
parameter (by default std::string); a template non-type parameter
(by default having value 12); and Policy itself expects a template
template parameter, called Inner, by default using an int as
its template type parameter.
Policy could be used as a base class of the class
Storage.
The policy operates on the class Storage's data type. Therefore the
policy is informed about that data type as well. Our class Storage now
begins like this:
template <typename Data, template <typename> class Policy>
class Storage: public Policy<Data>
This automatically allows us to use Policy's members when implementing
the members of the class Storage.
Our home-made allocation classes do not really provide us with many useful
members. Except for the extraction operator they offer no immediate access to
the data. This can easily be repaired by adding more members. E.g., the class
NewAlloc could be augmented with operators allowing access to and
modification of stored data:
operator Data &() // optionally add a `const' member too
{
return *d_data;
}
NewAlloc &operator=(Data const &data)
{
*d_data = data;
}
The other allocation classes could be given comparable members.
Let's use the allocation schemes in some real code. The next
example shows how Storage can be defined using some data type and an
allocation scheme. We start out again with a class Storage:
template <typename Data, template <typename> class Allocate>
class Storage: public std::vector<Data, Allocate<Data>>
{};
That's all we have to do. Note that std::vector formally has two
template parameters. The first one is the vector's data type, which is always
specified; the second one is the allocator used by the vector. Usually the
allocator is left unspecified (in which case the default STL allocator is
used), but here it is mentioned explicitly, allowing us to pass our own
allocation policy to Storage.
All required functionality is inherited from the vector base class, while
the policy is `factored into the equation' using a template template
parameter. Here's an example showing how this is done:
Storage<std::string, NewAlloc> storage;
copy(istream_iterator<std::string>(cin), istream_iterator<std::string>(),
back_inserter(storage));
cout << "Element index 1 is " << storage[1] << '\n';
storage[1] = "hello";
copy(storage.begin(), storage.end(),
ostream_iterator<NewAlloc<std::string> >(cout, "\n"));
Since Storage objects are also std::vector objects the STL copy
function can be used in combination with the back_inserter iterator to add
some data to the storage object. Its elements can be accessed and modified
using the index operator. Then NewAlloc<std::string> objects are inserted
into cout (also using the copy function).
Interestingly, this is not the end of the story. Remember that our
intention was to create a class allowing us to specify the storage type as
well. What if we don't want to use a vector, but instead would like to use
a list?
It's easy to change Storage's setup so that a completely different
storage type can be used on request, like a deque. To implement this, the
storage class is parameterized as well, using yet another template template
parameter:
template <typename Data, template <typename> class AllocationPolicy,
template <typename, typename> class Container = std::vector>
class Storage: public Container<Data, AllocationPolicy<Data>>
{};
The earlier example using a Storage object can be used again without
requiring any modifications at all (except for the above redefinition). It
clearly can't be used with a list container, as the list lacks
operator[]. Trying to do so is immediately recognized by the compiler,
producing an error if an attempt is made to use operator[] on, e.g., a
list. (A complete example showing the definition of the
allocation classes and the class Storage as well as its use is provided in
the C++ Annotations's distribution in the file
yo/advancedtemplates/examples/storage.cc.) A list container, however
can still be specified as the container to use. In that case a Storage is
implemented as a list, offering list's interface, rather than
vector's interface, to its users.
This situation, although legal, should be avoided for various reasons:
vtable is
required as well as a data member pointing to the vtable;
By providing a well-defined interface a class derived from a policy class may
define member specializations using the different structures of policy classes
to their advantage. For example, a plain pointer-based policy class could
offer its functionality by resorting to C-style pointer juggling,
whereas a vector-based policy class could use the vector's members
directly.
In this example a generic class template Size could be designed
expecting a container-like policy using features commonly found in
containers, defining the data (and hence the structure) of the container
specified in the policy. E.g.:
template <typename Data, template <typename> class Container>
struct Size: public Container<Data>
{
size_t size()
{ // relies on the container's `size()'
// note: can't use `this->size()'
return Container<Data>::size();
}
};
A specialization can now be defined for a much simpler storage class
using, e.g., plain pointers (the implementation capitalizes on first and
second, data members of std::pair. Cf. the example at the end of this
section):
template <typename Data>
struct Size<Data, Plain>: public Plain<Data>
{
size_t size()
{ // relies on pointer data members
return this->second - this->first;
}
};
Depending on the intentions of the template's author other members could be implemented as well.
To simplify the real use of the above templates, a generic wrapper class
can be constructed: it uses the Size template matching the actually used
storage type (e.g., a std::vector or some plain storage class) to define
its structure:
template <typename Data, template <typename> class Store>
class Wrapper: public Size<Data, Store>
{};
The above classes could now be used as follows (en passant showing an
extremely basic Plain class):
#include <iostream>
#include <vector>
template <typename Data>
struct Plain: public std::pair<Data *, Data *>
{};
int main()
{
Wrapper<int, std::vector> wiv;
std::cout << wiv.size() << "\n";
Wrapper<int, Plain> wis;
std::cout << wis.size() << "\n";
}
The wiv object now defines vector-data, the wis object merely
defines a std::pair object's data members.
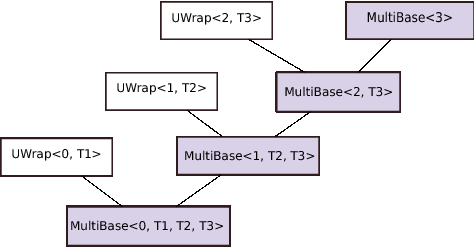
Alias templates can be used as arguments to template template
parameters. This allows us to avoid the `unexpected default parameters' you
may encounter when using template template parameters. E.g., defining a
template specifying a template <typename> class Container is fine, but it
is impossible to specify a container like vector or set as template
template argument, as vector and set containers also define a second
template parameter, specifying their allocation policy.
Alias templates are defined like using declarations, specifying an alias
for an existing (maybe partially or fully specialized) template type. In the
following example Vector is defined as an alias for vector:
template <typename Type>
using Vector = std::vector<Type>;
Vector<int> vi; // same as std::vector<int>
std::vector<int> vi2(vi); // copy construction: OK
So, what's the point of doing this?
Looking at the vector container, we see that it defines two, rather
than one, template parameters, the second parameter being the allocation
policy _Alloc, by default set to std::allocator<_Tp>:
template<typename _Tp, typename _Alloc = std::allocator<_Tp> >
class vector: ...
Now define a class template Generic defining a template template
parameter:
template <typename Type, template <typename> class Container>
class Generic: public Container<Type>
{
...
};
Most likely, Generic offers members made available by the container
that is actually used to create the Generic object, and adds to those some
members of it own. However, a simple container like std::vector cannot be
used, as std::vector doesn't match a template <typename> class
Container> parameter; it requires a template <typename, typename> class
Container> template template parameter.
The Vector alias template, however, is defined as a template
having one template type parameter, and it uses the vector's default
allocator. Consequently, passing a Vector to Generic works fine:
Generic<int, Vector> giv; // OK
Generic<int, std::vector> err; // won't compile: 2nd argument mismatch
With the aid of a small alias template it is also possible to use a
completely different kind of container, like a map, with Generic:
template <typename Type>
using MapString = std::map<Type, std::string>;
Generic<int, MapString> gim; // uses map<int, string>
std namespace
trait classes are found. E.g., most C++ programmers have seen
the compiler mentioning `std::char_traits<char>' when performing an
illegal operation on std::string objects, as in std::string s(1).
Trait classes are used to make compile-time decisions about types. Trait
classes allow us to apply the proper code to the proper data type, be it a
pointer, a reference, or a plain value, all this maybe in combination with
const. The particular type of data to use can be inferred from the actual
type that is specified (or implied) when the template is used. This can be
fully automated, not requiring the template writer to make any decision.
Trait classes allow us to develop a template <typename Type1, typename
Type2, ...> without the need to specify many specializations covering all
combinations of, e.g., values, (const) pointers, or (const) references, which
would soon result in an unmaintainable exponential explosion of template
specializations (e.g., allowing these five different types for each template
parameter already results in 25 combinations when two template type parameters
are used: each must be covered by potentially different specializations).
Having available a trait class, the actual type can be inferred compile
time, allowing the compiler to deduce whether or not the actual type is a
pointer, a pointer to a member, or a const pointer, and to make comparable
deductions in case the actual type is, e.g., an lvalue or rvalue reference
type. This in turn allows us to write templates that define types like
argument_type, first_argument_type, second_argument_type and
result_type, which are required by several generic algorithms (e.g.,
count_if()).
A trait class usually performs no behavior. I.e., it has no constructor
and no members that can be called. Instead, it defines a series of types and
enum values that have certain values depending on the actual type that is
passed to the trait class template. The compiler uses one of a set of
available specializations to select the one appropriate for an actual template
type parameter.
The point of departure when defining a trait template is a plain
vanilla struct, defining the characteristics of a plain value type like
an int. This sets the stage for specific specializations, modifying the
characteristics for any other type that could be specified for the template.
To make matters concrete, assume the intent is to create a trait class
BasicTraits telling us whether a type is a plain value type, a pointer
type, an lvalue reference type or an rvalue reference type (all of which may
or may not be const types).
Whatever the actually provided type, we want to be able to determine the `plain' type (i.e., the type without any modifiers, pointers or references), the `pointer type' and the `reference type', allowing us to define in all cases, e.g., an rvalue reference to its built-in type, even though we passed a const pointer to that type.
Our point of departure, as mentioned, is a plain struct defining the
required parameter. Maybe something like this:
template <typename T>
struct Basic
{
using Type = T;
enum
{
isPointer = false,
isConst = false,
isRef = false,
isRRef = false
};
};
Although some conclusions can be drawn by combining various enum
values (e.g., a plain type is not a pointer or a reference or an rvalue
reference or a const), it is good practice to provide a full implementation of
trait classes, not requiring its users to construct these logical expressions
themselves. Therefore, the basic decisions in a trait class are usually made
by a
nested trait class,
leaving the task of creating appropriate logical expressions to a
surrounding trait class.
So, the struct Basic defines the generic form of our inner trait
class. Specializations handle specific details. E.g., a pointer type is
recognized by the following specialization:
template <typename T>
struct Basic<T *>
{
using Type = T;
enum
{
isPointer = true,
isConst = false,
isRef = false,
isRRef = false
};
};
whereas a pointer to a const type is matched with the next specialization:
template <typename T>
struct Basic<T const *>
{
using Type = T;
enum
{
isPointer = true,
isConst = true,
isRef = false,
isRRef = false
};
};
Several other specializations should be defined: e.g., recognizing
const value types or (rvalue) reference types. Eventually all these
specializations are implemented as nested structs of an outer class
BasicTraits, offering the public traits class interface. The outline of
the outer trait class is:
template <typename TypeParam>
class BasicTraits
{
// Define specializations of the template `Base' here
public:
BasicTraits(BasicTraits const &other) = delete;
using ValueType = Basic<TypeParam>::Type;
using PtrType = ValueType *;
using RefType = ValueType &;
using RvalueRefType = ValueType &&;
enum
{
isPointerType = Basic<TypeParam>::isPointer,
isReferenceType = Basic<TypeParam>::isRef,
isRvalueReferenceType = Basic<TypeParam>::isRRef,
isConst = Basic<TypeParam>::isConst,
isPlainType = not (isPointerType or isReferenceType or
isRvalueReferenceType or isConst)
};
};
The trait class's public interface explicitly deletes its copy constructor. As it therefore defines no constructor at all and as it has no static members it does not offer any run-time executable code. All the trait class's facilities must therefore be used compile time.
A trait class template can be used to obtain the proper type, irrespective
of the template type argument provided. It can also be used to select
a proper specialization that depends on, e.g., the const-ness of a
template type. Example:
cout <<
"int: plain type? " << BasicTraits<int>::isPlainType << "\n"
"int: ptr? " << BasicTraits<int>::isPointerType << "\n"
"int: const? " << BasicTraits<int>::isConst << "\n"
"int *: ptr? " << BasicTraits<int *>::isPointerType << "\n"
"int const *: ptr? " << BasicTraits<int const *>::isPointerType <<
"\n"
"int const: const? " << BasicTraits<int const>::isConst << "\n"
"int: reference? " << BasicTraits<int>::isReferenceType << "\n"
"int &: reference? " << BasicTraits<int &>::isReferenceType << "\n"
"int const &: ref ? " << BasicTraits<int const &>::isReferenceType <<
"\n"
"int const &: const ? " << BasicTraits<int const &>::isConst << "\n"
"int &&: r-reference? " << BasicTraits<int &&>::isRvalueReferenceType <<
"\n"
"int &&: const? " << BasicTraits<int &&>::isConst << "\n"
"int const &&: r-ref ? "<< BasicTraits<int const &&>::
isRvalueReferenceType << "\n"
"int const &&: const ? "<< BasicTraits<int const &&>::isConst << "\n"
"\n";
BasicTraits<int *>::ValueType value = 12;
BasicTraits<int const *>::RvalueRefType rvalue = int(10);
BasicTraits<int const &&>::PtrType ptr = new int(14);
cout << value << ' ' << rvalue << ' ' << *ptr << '\n';
BasicTraits trait class was developed. Using
specialized versions of a nested struct Type modifiers, pointers,
references and values could be distinguished.
Knowing whether a type is a class type or not (e.g., the type represents a primitive type) could also be a useful bit of knowledge to a template developer. The class template developer might want to define a specialization when the template's type parameter represents a class type (maybe using some member function that should be available) and another specialization for non-class types.
This section addresses the question how a trait class can distinguish class types from non-class types.
In order to distinguish classes from non-class types a distinguishing feature that can be used at compile-time must be found. It may require some thinking to find such a distinguishing characteristic, but a good candidate eventually is found in the pointer to members syntactic construct. Pointers to members are only available for classes. Using the pointer to member construct as the distinguishing characteristic, a specialization can be developed that uses the pointer to member if available. Another specialization (or the generic template) does something else if the pointer to member construction is not available.
How can we distinguish a pointer to a member from `a generic situation', not being a pointer to a member? Fortunately, such a distinction is possible. A function template specialization can be defined having a parameter which is a pointer to a member function. The generic function template then accepts any other argument. The compiler selects the former (specialized) function when the provided type is a class type as class types may support a pointer to a member. The interesting verb here is `may': the class does not have to define a pointer to member.
Furthermore, the compiler does not actually call any function: we're talking compile-time here. All the compiler does is to select the appropriate function by evaluating a constant expression.
So, our intended function template now looks like this:
template <typename ClassType>
static `some returntype' fun(void (ClassType::*)());
The function's return type (`(some returntype)') will be defined
shortly. Let's first have a closer look at the function's parameter. The
function's parameter defines a pointer to a member returning void. Such a
function does not have to exist for the concrete class-type that's
specified when the function is used. In fact, no implementation is
provided. The function fun is only declared as a static member in the
trait class. It's not implemented and no trait class object is required to
call it. What, then, is its use?
To answer the question we now have a look at the generic function template that should be used when the template's argument is not a class type. The language offers a `worst case' parameter in its ellipsis parameter list. The ellipsis is a final resort the compiler may turn to if everything else fails. The generic function template specifies a plain ellipsis in its parameter list:
template <typename NonClassType>
static `some returntype' fun(...);
It would be an error to define the generic alternative as a function
expecting an int. The compiler, when confronted with alternatives,
favors the simplest, most specified alternative over a more complex, generic
one. So, when providing fun with an argument it selects int
whenever possible and it won't select fun(void (ClassType::*)()). When
given the choice between fun(void (ClassType::*)()) and fun(...) it
selects the former unless it can't do that.
The question now becomes: what argument can be used for both a pointer to a member and for the ellipsis? Actually, there is such a `one size fits all' argument: 0. The value 0 can be passed as argument value to functions defining an ellipsis parameter and to functions defining a pointers-to-member parameter.
But 0 does not specify a particular class. Therefore, fun must specify
an explicit template argument, appearing in our code as fun<Type>(0), with
Type being the template type parameter of the trait class.
Now for the return type. The function's return type cannot be a simple
value (like true or false). Our eventual intent is to provide the
trait class with an enum telling us whether the trait class's template
argument represents a class type or not. That enum becomes something like
this:
enum { isClass = some class/non-class distinguishing expression } ;
The distinguishing expression cannot be
enum { isClass = fun<Type>(0) } ;
as fun<Type>(0) is not a constant expression and enum values must
be defined by constant expressions so they can be determined at compile-time.
To determine isClass's value we must find an expression allowing for
compile-time discriminations between fun<Type>(...) and fun<Type>(void
(Type::*)()).
In situations like these the sizeof operator often is our tool of
choice as it is evaluated at compile-time. By defining different sized return
types for the two fun declarations we are able to distinguish (at
compile-time) which of the two fun alternatives is selected by the
compiler.
The char type is by definition a type having size 1. By defining
another type containing two consecutive char values a larger type is
obtained. A char [2] is of course not a type, but a char[2] can be
defined as a data member of a struct, and a struct does define a
type. That struct then has a size exceeding 1. E.g.,
struct Char2
{
char data[2];
};
Char2 can be defined as a nested type of our traits class. The
two fun function template declarations become:
template <typename ClassType>
static Char2 fun(void (ClassType::*)());
template <typename NonClassType>
static char fun(...);
Since sizeof expressions are evaluated at compile-time we can now
determine isClass's value:
enum { isClass = sizeof(fun<Type>(0)) == sizeof(Char2) };
This expression has several interesting implications:
fun function template is ever instantiated;
Type and selects
fun's function template specialization if Type is a class type and the
generic function template if not;
isClass.
<type_traits> header file must be
included.
All facilities offered by type_traits are defined in the std
namespace (omitted from the examples given below), allowing programmers to
determine various characteristics of types and values.
In the description of available type traits the following concepts are encountered:
void or objects;
void, to objects, to functions, or to
non-static class members;
bool
and all built-in types representing (possibly unicode) characters;
false
unless noexcept(true) is used at the function's declaration. E.g.,
struct NoThrow
{
NoThrow &operator=(SomeType const &rhs) noexept(true);
};
constexpr constructor other than the copy or move
constructor, and only has non-static data members and base classes of
literal types;
default) in
their class interfaces and (for default constructors or assignment
operators) only perform byte-by-byte actions. Here are two examples:
struct Pod only has trivial members as it doesn't explicitly
declare any member function and its data member is plain old
data. struct Nonpod is not plain old data. Although it
doesn't explictly declare any member function either, its data member
is a std::string, which itself isn't plain old data as
std::string has non-trivial constructors:
struct Pod
{
int x;
};
struct Nonpod
{
std::string s;
};
When type-condition applies to a type, it must be a complete type,
void, or an array of unknown size;
The following type traits are provided:
add_const<typename Type>::type
to add const to Type;
add_cv<typename Type>::type
to add const volatile to Type;
add_lvalue_reference<typename Type>::type
to add an lvalue reference to Type;
add_pointer<typename Type>::type
to add a pointer to Type;
add_rvalue_reference<typename Type>::type
to add an rvalue reference to Type;
add_volatile<typename Type>::type
to add volatile to Type;
conditional<bool cond, typename TrueType, typename FalseType>::type
to conditionally use TrueType if cond is true,
FalseType if not;
template <typename Type> struct decay
defines the typename type obtained from Type after
removing all cv-qualifiers and references from the specified template
type argument. Moreover, it converts lvalue types to rvalue types,
and arrays and functions to pointers. It resembles what happens if an
argument is passed to a value-type parameter.
template <typename Type> decay_t
is shorthand for typename decay<Type>::type.
enable_if<bool cond, typename Type>::type
to conditionally define Type if cond is true;
is_abstract<typename Type>::value
to determine whether Type is an abstract type
(e.g., an abstract base class) (type-condition applies);
is_arithmetic<typename Type>::value
to determine whether Type is an arithmetic type;
is_array<typename Type>::value
to determine whether Type is an array type;
is_assignable<typename To, typename From>::value
to determine whether an object of type From can
be assigned to an object of type To (type-condition applies);
is_base_of<typename Base, typename Derived>::value
to determine whether Base is a base class
of type Derived;
is_class<typename Type>::value
to determine whether Type is a class type;
is_compound<typename Type>::value
to determine whether Type is a compound type;
is_const<typename Type>::value
to determine whether Type is a const type;
is_constructible<typename Type, typename ...Args>::value
to determine whether Type is constructible
from arguments in the Args parameter pack (type-condition
applies to all types in Args);
is_convertible<typename From, typename To>::value
to determine whether a type From may be
converted to a type To using a static_cast;
is_copy_assignable<typename Type>::value
to determine whether Type supports copy
assignment (type-condition applies);
is_copy_constructible<typename Type>::value
to determine whether Type supports copy
construction (type-condition applies);
is_default_constructible<typename Type>::value
to determine whether Type supports a
default constructor (type-condition applies);
is_destructible<typename Type>::value
to determine whether Type has a non-deleted
destructor (type-condition applies);
is_empty<typename Type>::value
to determine whether Type is a class type (not a union
type), without non-static data members, virtual members, virtual or
non-empty base classes (type-condition applies);
is_enum<typename Type>::value
to determine whether Type is an enum type;
is_floating_point<typename Type>::value
to determine whether Type is a floating point
type;
is_function<typename Type>::value
to determine whether Type is a function type;
is_fundamental<typename Type>::value
to determine whether Type is a fundamental type;
is_integral<typename Type>::value
to determine whether Type is an integral type;
is_literal_type<typename Type>::value
to determine whether Type is a literal type
(type-condition applies);
is_lvalue_reference<typename Type>::value
to determine whether Type is an lvalue
reference;
is_member_function_pointer<typename Type>::value
to determine whether Type is a
pointer to a non-static member function;
is_member_object_pointer<typename Type>::value
to determine whether Type is a pointer
to a non-static data member;
is_member_pointer<typename Type>::value
to determine whether Type is a pointer to a
member function;
is_move_assignable<typename Type>::value
to determine whether Type supports move
assignment (type-condition applies);
is_move_constructible<typename Type>::value
to determine whether Type supports move
construction (type-condition applies);
is_nothrow_assignable<typename To, typename From>::value
to determine whether Type supports an
assignment operator not throwing exceptions (type-condition
applies).
is_nothrow_constructible<typename Type, typename ...Args>::value
to determine whether a Type object can
be constructed from arguments of types mentioned in the parameter pack
not throwing exceptions (type-condition applies);
is_nothrow_copy_assignable<typename Type>::value
to determine whether Type supports a
copy-assignment operator not throwing exceptions (type-condition
applies);
is_nothrow_copy_constructible<typename Type>::value
to determine whether Type
supports copy construction not throwing exceptions (type-condition
applies);
is_nothrow_default_constructible<typename Type>::value
to determine whether Type
supports a default constructor not throwing exceptions
(type-condition applies);
is_nothrow_destructible<typename Type>::value
to determine whether Type supports a
destructor not throwing exceptions (type-condition applies).
is_nothrow_move_assignable<typename Type>::value
to determine whether Type supports
move assignment not throwing exceptions (type-condition applies);
is_nothrow_move_constructible<typename Type>::value
to determine whether Type
supports a move constructor not throwing exceptions
(type-condition applies);
is_object<typename Type>::value
to determine whether Type is an object (in contrast
to scalar) type;
is_pod<typename Type>::value
to determine whether Type is an aggregate
(plain old data,
type-condition applies);
is_pointer<typename Type>::value
to determine whether Type is a pointer type;
is_polymorphic<typename Type>::value
to determine whether Type is a polymorphic type
(type-condition applies);
is_reference<typename Type>::value
to determine whether Type is an (lvalue or rvalue)
reference;
is_rvalue_reference<typename Type>::value
to determine whether Type is an rvalue
reference;
is_same<typename First, typename Second>::value
to determine whether types First and Second are
identical;
is_scalar<typename Type>::value
to determine whether Type is a scalar type (in
contrast to an object type);
is_signed<typename Type>::value
to determine whether Type is a signed type;
is_standard_layout<typename Type>::value
to determine whether Type offers the
standard layout (type-condition applies);
is_trivial<typename Type>::value
to determine whether Type is a trivial type
(type-condition applies);
is_trivially_assignable<typename Dest, typename Src>::value
to determine whether an object or value of
type Src can trivially be assigned to an object of type Dest
(type-condition applies);
is_trivially_constructible<typename Type, typename ...Args>::value
to determine whether Type is
trivially constructible from arguments in the Args parameter pack
(type-condition applies to all types in Args);
is_trivially_copy_assignable<typename Type>::value
to determine whether Type supports
a trivial assignment operator (type-condition applies);
is_trivially_copy_constructible<typename Type>::value
to determine whether Type is
trivially copy-constructible (type-condition applies);
is_trivially_copyable<typename Type>::value
to determine whether Type is trivially
copyable (type-condition applies);
is_trivially_default_constructible<typename Type>::value
to determine whether Type
supports a trivial default constructor (type-condition applies);
is_trivially_default_destructible<typename Type>::value
to determine whether Type
supports a trivial default destructor (type-condition applies);
is_trivially_move_assignable<typename Type>::value
to determine whether Type supports
a trivial assignment operator (type-condition applies);
is_trivially_move_constructible<typename Type>::value
to determine whether Type is
trivially move-constructible (type-condition applies);
is_union<typename Type>::value
to determine whether Type is a union type;
is_unsigned<typename Type>::value
to determine whether Type is an unsigned type;
is_void<typename Type>::value
to determine whether Type is void;
is_volatile<typename Type>::value
to determine whether Type is a volatile
qualified type;
make_signed<typename Type>::type
to construct a signed type;
make_unsigned<typename Type>::type
to construct an unsigned type;
remove_all_extents<typename Type>::type
if Type is a (possibly multidimensional)
array of ElementType values or objects then typedef type
equals ElementType;
remove_const<typename Type>::type
to remove const from Type;
remove_cv<typename Type>::type
to remove const and/or volatile from Type;
remove_extent<typename Type>::type
if Type is an array of ElementType values or
objects then typedef type equals ElementType. With
multi-dimensional arrays ElementType is the type of the array from
which its first array dimension has been removed;
remove_pointer<typename Type>::type
to remove a pointer from Type;
remove_reference<typename Type>::type
to remove a reference from Type;
remove_volatile<typename Type>::type
to remove volatile from Type;
std::error_code was introduced. One of
its constructors accepts ErrorCodeEnum values, where ErrorCodeEnum is
a template type name for enumerations that we may define ourselves containing
symbols that are used as error code values. Another constructor expects an
int-valued error code and a specification of an error category that uses
those error codes.
Several error code enumerations and error categories are predefined by C++
but it is also possible to define new ErrorCodeEnums and error
categories. In this section constructing new ErrorCodeEnums is covered, in
the next section designing new error categories is covered.
Defining new error code enumerations is an option when using error_code
objects is attractive, but standard error code values (like the values defined
by enum class errc) aren't appropriate. For example, when designing an
interactive calculator, several errors may be encountered that are related to
the way expressions are entered by the user. For those situations you might
want to develop your own error code enumeration.
In this and the next section a bare bones approach to defining error code enumerations and error categories is adopted. No concrete, real-life like class is developed. I think the advantage of this is that this way it's easier to apply the principles to new real-life situations than if you first have to abstract the content of a real-life example yourself. Here we go:
The enum class CatErr lists causes of errors that are associated
with our (as yet to be designed) error category:
enum class CatErr
{
Err1 = 1, // causes of errors
Err2,
Err3
};
enum class does not allow us to pass its
values to error_code constructors. Before we can do that the enum
must be `promoted' to an error_code_enum. This `promotion' is
realized by specializing the trait class
std::is_error_code_enum after which the
error_code(ErrorCodeEnum) member template and the make_error_code
function accept CatErr enumeration values. Interestingly, this
requires us to add code to the std namespace. Normally this is not
allowed, but in this case it is. The C++ standard states:
20.5.4.2.1 Namespace stdThe behavior of a C++ program is undefined if it adds declarations or definitions to namespace std or to a namespace within namespace std unless otherwise specified.
A program may add a template specialization for any standard library template to namespace std only if the declaration depends on a user-defined type and the specialization meets the standard library requirements for the original template and is not explicitly prohibited.
Here is how the is_error_code_enum trait class is specialized:
namespace std
{
template <>
struct is_error_code_enum<CatErr>: public true_type
{};
}
This completes the definition of our own error code enumeration, whose symbols
are now accepted by error_code's constructor.
Before we're able to design our own error category we must also have a look at
`higher order' causes of errors as represented by objects of the class
std::error_condition (cf. section 10.9.2). Error conditions
represent platform independent errors like syntax errors or non-existing
requests.
In our bare bones implementation of an error category these higher order
causes of errors are enumerated in the enum class Cond enumeration. It's
defined similarly to CatErr.
Cond whose symbols presumably represent platform
independent causes of errors:
enum class Cond
{
NoCond = -1,
Cond1 = 1,
Cond2,
Cond3,
};
enum class does not allow us to pass its
values to error_condition constructors. Before we can do that the
enum must be `promoted' to an error_condition_enum. Also similar
to CatErr this `promotion' is realized by specializing the trait class
std::is_error_condition_enum
Here is how the is_error_condition_enum trait class is specialized:
namespace std
{
template <>
struct is_error_condition_enum<Cond>: public true_type
{};
}
We're now ready for designing our own error_category class.
CatErr and Cond
were developed. The values of these enumerations specify, respectively, the
direct and the platform independent causes of errors that may be encountered
in the context of the new error category developed in this section.
Classes derived from std::error_category are designed as singleton classes
and implement their own name, message and an equivalent members. Our
class Category also declares a static member instance returning a
reference to the class's singleton object, which is compile-time initialized
and is available by the time instance is called. Alternatively a dedicated
function (like Category_category), analogously to the function
generic_category, returning a reference to the Category object could
be defined.
CatErr values, Cond values and textual descriptions of CatErr's
values are combined in a std::unordered_map using CatErr as key, and a
struct POD as value type. This map allows us to retrieve the platform
independent error types and the descriptions that are associated with
CatErr values.
Here is the interface of the class Category:
class Category: public std::error_category
{
static Category s_instance;
struct POD
{
Cond cond;
char const *msg;
};
static std::unordered_map<CatErr, POD> s_map;
public:
Category(Category const &other) = delete;
static Category &instance();
bool equivalent(std::error_code const &ec, int condNr)
const noexcept override;
bool equivalent(int ev, std::error_condition const &condition)
const noexcept override;
std::error_condition default_error_condition(int ev)
const noexcept override;
std::string message(int ce) const override;
char const *name() const noexcept override;
private:
Category() = default;
template <typename Enum>
static constexpr Enum as(int err);
};
Its unordered_map s_map provides the Cond values and verbal
descriptions of the CatErr values given those CatErr values:
unordered_map<CatErr, Category::POD> Category::s_map =
{
{ CatErr::Err1, { Cond::Cond1, "Err1" } },
{ CatErr::Err2, { Cond::Cond2, "Err2" } },
{ CatErr::Err3, { Cond::Cond1, "Err3" } },
};
The functions make_error_code and make_error_condition return,
respectively, error_code and error_condition objects from,
respectively, CatErr values and Cond values.
Their declarations can be provided below the Category class interface and
their implementations pass the Category object to their constructors:
std::error_code make_error_code(CatErr ce)
{
return { static_cast<int>(ce), Category::instance() };
}
std::error_condition make_error_condition(Cond ec)
{
return { static_cast<int>(ec), Category::instance() };
}
The member name must be defined by classes derived from
error_category. It simply returns a short string naming the category
(e.g., "Category" for our Category class). Likewise, the member
message must be redefined. Its implementation usually is slightly more
complex than name's implementation: it expects a (cast to an int)
CatErr value and uses that value to find the corresponding textual
description in s_map. If found the description is returned; if not found
then a short fallback message is returned:
std::string Category::message(int ce) const
{
auto iter = s_map.find(static_cast<CatErr>(ce));
return iter != s_map.end() ? iter->second.msg : "No CatErr value";
}
The member default_error_condition receives a (cast to int) CatErr
value. That value is used to find the associated Cond value. If the
int received by the function does not represent a valid CatErr value
then the fallback value Cond::NoCond is used. The function returns an
error_condition object created by make_error_condition which receives
the determined Cond value as its argument:
std::error_condition Category::default_error_condition(int ev)
const noexcept
{
auto iter = s_map.find(as<CatErr>(ev));
return make_error_condition(
iter == s_map.end() ? Cond::NoCond : iter->second.cond
);
}
What's left is implementing the two equivalent members. The first
equivalent member (receiving a reference to an error_code object and a
(cast to int) Cond value) determines the equivalence of
the Cond value that is associated with the error_code object
and
the Cond value that is specified as the function's second argument.
If these values are equal and the error_code object's category is equal
to Category then the equivalence has been established and true is
returned. Here is its implementation:
bool Category::equivalent(std::error_code const &ec, int condNr)
const noexcept
{
if (*this != ec.category())
return false;
if (ec.value() == 0) // no error in ec?
return condNr == 0; // then condNr must
// also be 0
auto iter = s_map.find(as<CatErr>(ec.value())); // info associated
// with ec's CatErr
return iter == s_map.end() ?
false // not found or
: // compare Cond values
iter->second.cond == as<Cond>(condNr);
}
The second equivalent member (receiving (as an int) CatErr value
and an error_condition object) determines the equivalence of an
error_condition object that is constructed from the Cond value
that is associated with the CatErr value that was passed (as int)
to the function
and
the error_condition object that was passed to the function as its
second argument.
Here a prerequisite for concluding equivalence is that the error condition's
category is Category. If that's the case then the function returns
true if its int argument equals zero and the condition object also
indicates no error. Alternatively, if the condition argument is equal to
the error_condition object made from the Cond value associated with
the CatErr value passed to the function as its first argument the
equivalence has also been established and true is returned. Here is its
implementation:
bool Category::equivalent(int ev, error_condition const &condition)
const noexcept
{
if (ev == 0) // no error? then
return condition.category() == *this and // categories must
not static_cast<bool>(condition); // be equal and
// condition must
// indicate no error
auto iter = s_map.find(as<CatErr>(ev)); // find ev's Cond
return iter == s_map.end()?
false // no such CatErr
: // or compare conditions
condition == make_error_condition(iter->second.cond);
}
So, in order to define your own category:
error_code_enum;
error_condition_enum;
error_category class by deriving a class from
std::error_category, define it as a singleton class and override
its default_error_condition, equivalent, message, and name
members.
The actions in the first step might be made move aware by using
std::move (e.g., to assign the source's values to a (possibly temporary)
destination). However, using std::move can easily affect the source (e.g.,
when extending the source's memory, moving the existing data to its new
locations), which breaks the first step's assumption, as the target object is
now modified.
In this case (and generally) the move operation should not be allowed to throw exceptions. This, in turn, implies that it is difficult to write code which must offer a non-throwing moving constructor, if it uses (external) data types over which the moving constructor has no control. E.g.,
template <typename Type>
class MyClass
{
Type d_f;
public:
MyClass() = default;
MyClass(MyClass &&tmp)
:
d_f(move(tmp.d_f))
{}
};
Here, MyClass's author has no control over the design of Type. If
Foreign merely has a (possibly throwing) copy constructor, then the
following code breaks the no-throw assumption underlying move constructors:
MyClass<Foreign> s2{ move(MyClass<Foreign>()) };
If templates are able to detect whether Type has non-throwing move
constructors then their implementations may be optimized by
calling these move constructors (already modifying their targets in the first
part of code offering the strong guarantee) in situations where otherwise the
non-modifying, but more expensive copy constructor has to be used.
The noexcept keyword was introduced to allow such templates to perform
such optimizations. As with throw lists, checking for noexcept is
a run-time check, but the consequence of violating a noexept declaration
are more serious than violating a throw list: violating noexcept
results in calling std::terminate, terminating the program, possibly
without unwinding the stack. In the context of the previous example, the
following code is flawlessly accepted by the compiler, demonstrating that
there is no compile-time checking of noexcept:
class Foreign
{
public:
Foreign() = default;
Foreign(Foreign const &other) noexcept
{
throw 1;
}
};
However, when this class's copy constructor is called, execution aborts with the following message:
terminate called after throwing an instance of 'int'
Abort
Keep in mind that the current purpose of noexcept is to allow templates to
optimize their code by using move operations where the code must also be able
to offer the string exception guarantee. Since noexcept also offers the
conditional noexcept(condition) syntax (with noexcept(true) and
noexcept having identical semantics), noexcept can be made
conditional to the `noexcepting' nature of template types. Note that this is
not possible with throw lists.
The following rules of thumb by be used to decide whether or
not to use noexcept in your code:
noexcept (this is identical to the advise
given for throw lists);
noexcept(true) if the
compiler can deduce that composing types also offer
noexcept(true), allowing template optimizations using move
operations where possible.
noexcept declarations may still throw
exceptions (see the example given above). In the end noexcept
merely means that if such a function throws an exception
std::terminate rather tha std::unexpected is called.
throw())
should be provided with noexcept.
noexcept specifications are required when using the following std
traits (declared in the <type_traits> header file):
is_nothrow_constructible
is_nothrow_default_constructible
is_nothrow_move_constructible
is_nothrow_copy_constructible
is_nothrow_assignable
is_nothrow_move_assignable
is_nothrow_copy_assignable
is_nothrow_destructible
value which is
true if the class (and possibly its argument type list) matches
the characteristic after which the trait was named. E.g., if
MyClass(string const &) noexcept is a constructor, then
std::is_nothrow_constructible<MyClass, string>::value
equals true. For the named members (like
is_nothrow_move_constructible) parameter types do not have to be
specified, as they are implied. E.g.,
std::is_nothrow_move_constructible<MyClass>::value
returns true if the move constructor has the noexcept
modifier.
transform generic algorithm (cf. section 19.1.64):
template <typename Return, typename Argument>
Return chop(Argument const &arg)
{
return Return{ arg };
}
Furthermore assume that if Return is std::string then the above
implementation should not be used. Instead, with std::string a second
argument 1 should always be provided. If Argument is a C++ string,
this would allow us to, e.g., return a copy of arg from which its first
character has been chopped off.
Since chop is a function, it is not possible to define a partial
specialization like this:
template <typename Argument> // This won't compile!
std::string chop<std::string, Argument>(Argument const &arg)
{
return std::string{ arg, 1 };
}
Although a function template cannot be partially specialized it is
possible to use overloading, defining a second, dummy, string parameter:
template <typename Argument>
std::string chop(Argument const &arg, std::string)
{
return std::string{ arg, 1 };
}
Instead of providing a string dummy argument the functions could
use the IntType template (cf. section 23.2.1.1) to select the proper
overloaded version. E.g., IntType<0> could be defined as the type of the
second argument of the first overloaded chop function, and IntType<1>
could be used for the second overloaded function. From the point of view of
program efficiency this is an attractive option, as the provided IntType
objects are extremely lightweight. IntType objects contain no data at
all. But there's also an obvious disadvantage as there is no intuitively clear
association between the int value used and the intended type.
Instead of defining arbitrary IntType types it is more attractive to
use another lightweight solution, using an automatic type-to-type
association. The struct TypeType is a lightweight type wrapper, much like
IntType. Here is its definition:
template <typename T>
struct TypeType
{
using Type = T;
};
TypeType is also a lightweight type as it doesn't have any data fields
either. TypeType allows us to use a natural type association for
chop's second argument. E.g, the overloaded functions can now be defined
as follows:
template <typename Return, typename Argument>
Return chop(Argument const &arg, TypeType<Argument> )
{
return Return{ arg };
}
template <typename Argument>
std::string chop(Argument const &arg, TypeType<std::string> )
{
return std::string{ arg, 1 };
}
Using the above implementations any type can be specified for
Result. If it happens to be a std::string the appropriate overloaded
version is automatically selected. The following additional overload of the
function chop capitalizes on this:
template <typename Result>
Result chop(char const *txt) // char const * could also be a 2nd
{ // template type parameter
return chop(std::string{ txt }, TypeType<Result>{});
}
Using the third chop function, the following statement produces the
text `ello world':
cout << chop<string>{ "hello world" } << '\n';
Template functions do not support partial specializations. But they can be overloaded. By providing overloads with dummy type-arguments that depend on other parameters and calling these overloads from a overloaded function that does not require the dummy type argument a situation similar to partial specializations with class templates can often be realized.
struct is a useful tool. It can be used as a type acting
analogously to the final 0-byte in NTBSs.
It can simply be defined as:
struct NullType
{};
T be used as a `stand in' for another type
U? Since C++ is a strongly typed language the answer is surprisingly
simple: Ts can be used instead of Us if a T is accepted as
argument in cases where Us are requested.
This reasoning is behind the following class which can be used to determine
whether a type T can be used where a type U is expected. The
interesting part is that no code is actually generated or executed. All
decisions are made by the compiler.
In the second part of this section we'll show how the code developed in
the first part can be used to detect whether a class B is a base class of
another class D (the is_base_of template (cf. section 23.6.2)
also provides an answer to this question). The code developed here closely
follows the example provided by Alexandrescu (2001,
p. 35).
First, a function test is designed accepting a type U.
The function test returns a value
of the as yet unknown type Convertible:
Convertible test(U const &);
The function test is never implemented. It is only declared. If a type
T can be used instead of a type U then T can also be passed as
argument to the above test function.
On the other hand, if the alternate type T cannot be used where a U is
expected, then the compiler won't be able to use the above test
function. Instead, it uses an alternative function that has a lower
selection priority but that can always be used with any T type.
C (and C++) offer a very general parameter list, a parameter list that is always considered acceptable. This parameter list is the familiar ellipsis which represents the worst case the compiler may encounter. If everything else fails, then the function defining an ellipsis as its parameter list is selected.
Usually that's not a productive alternative, but in the current situation it is exactly what is needed. When confronted with two candidate functions, one of which defines an ellipsis parameter, the compiler selects the function defining the ellipsis parameter only if the alternative(s) can't be used.
Following the above reasoning an alternative function test(...) is
declared as well. This alternate function does not return a Convertible
value but a NotConvertible value:
NotConvertible test(...);
If test's argument is of type T and if T can be converted to U
then test's return type is Convertible. Otherwise NotConvertible
is returned.
This situation clearly shows similarities with the situation encountered in
section 23.6.1 where the value isClass had to be determined
compile time. Here two related problems must be solved:
T argument? This is more difficult than might
be expected at first sight as it might not be possible to define a T. If
type T does not define any constructor then no T object can be
defined.
Convertible be distinguished from NotConvertible?
T needs to be
defined. After all, the intent is to decide compile-time whether a type is
convertible and not to define a T value or object. Defining objects is not
a compile-time but a run-time matter.
By simply declaring a function returning a T we can
tell the compiler where it should assume a T:
T makeT();
This mysterious function has the magical power of enticing the compiler
into thinking that a T object comes out of it. However, this function
needs a small modification before it will actually suit our needs. If, for
whatever reason, T happens to be an array then the compiler will choke on
T makeT() as functions cannot return arrays. This, however, is easily
solved, as functions can return references to arrays. So the above
declaration is changed into:
T const &makeT();
Next we pass a T const & to test:
following code:
test(makeT())
Now that the compiler sees test being called with a T const &
argument it decides that its return value is Convertible if a
conversion is in fact possible. Otherwise it decides that its return value
is NotConvertible (as the compiler, in that case, selected test(...)).
The second problem, distinguishing Convertible from NotConvertible
is solved exactly the way isClass could be determined in section
23.6.1, viz. by making their sizes different. Having done so the
following expression determines whether T is convertible from U or
not:
isConvertible = sizeof(test(makeT())) == sizeof(Convertible);
By using char for Convertible and Char2 (cf. section
23.6.1) for NotConvertible the distinction can be made.
The above can be summarized in a class template LconvertibleToR,
having two template type parameters:
template <typename T, typename U>
class LconvertibleToR
{
struct Char2
{
char array[2];
};
static T const &makeT();
static char test(U const &);
static Char2 test(...);
public:
LconvertibleToR(LconvertibleToR const &other) = delete;
enum { yes = sizeof(test(makeT())) == sizeof(char) };
enum { sameType = 0 };
};
template <typename T>
class LconvertibleToR<T, T>
{
public:
LconvertibleToR(LconvertibleToR const &other) = delete;
enum { yes = 1 };
enum { sameType = 1 };
};
As the class template deletes its copy constructor no object can be
created. Only its enum values can be interrogated. The next example writes
1 0 1 0 when run from a main function:
cout <<
LconvertibleToR<ofstream, ostream>::yes << " " <<
LconvertibleToR<ostream, ofstream>::yes << " " <<
LconvertibleToR<int, double>::yes << " " <<
LconvertibleToR<int, string>::yes <<
"\n";
Base is a (public) base class of a type
Derived.
Inheritance is determined by inspecting convertibility of (const)
pointers. Derived const * can be converted to Base const * if
Base is a public and unambiguous base class of Derived;
Base is void.
LBaseRDerived. LBaseRDerived provides
an enum yes which is 1 if the left type is a base class of the right type
and both types are different:
template <typename Base, typename Derived>
struct LBaseRDerived
{
LBaseRDerived(LBaseRDerived const &) = delete;
enum {
yes =
LconvertibleToR<Derived const *, Base const *>::yes &&
not LconvertibleToR<Base const *, void const *>::sameType
};
};
If code should not consider a class to be its own base class, then the
trait class LBaseRtrulyDerived can be used to perform a strict test. This
trait class adds a test for type-equality:
template <typename Base, typename Derived>
struct LBaseRtrulyDerived
{
LBaseRtrulyDerived(LBaseRtrulyDerived const &) = delete;
enum {
yes =
LBaseRDerived<Base, Derived>::yes &&
not LconvertibleToR<Base const *, Derived const *>::sameType
};
};
Example: the next statement displays 1: 0, 2: 1, 3: 0, 4: 1, 5: 0
when executed from a main function:
cout << "\n" <<
"1: " << LBaseRDerived<ofstream, ostream>::yes << ", " <<
"2: " << LBaseRDerived<ostream, ofstream>::yes << ", " <<
"3: " << LBaseRDerived<void, ofstream>::yes << ", " <<
"4: " << LBaseRDerived<ostream, ostream>::yes << ", " <<
"5: " << LBaseRtrulyDerived<ostream, ostream>::yes <<
"\n";
This section itself was inspired by Andrei Alexandrescu's (2001) book Modern C++ design. It diverts from Alexandrescu's book in its use of variadic templates which were not yet available when he wrote his book. Even so, the algorithms used by Alexandrescu are still useful when using variadic templates.
C++ offers the tuple to store and retrieve
values of multiple types. Here the focus is merely on processing types. A
simple struct TypeList is going to be used as our working horse for the
upcoming subsections. Here is its definition:
template <typename ...Types>
struct TypeList
{
TypeList(TypeList const &) = delete;
enum { size = sizeof ...(Types) };
};
A typelist allows us to store any number of types. Here is an example
storing the three types char, short, int in a TypeList:
TypeList<char, short, int>
sizeof
operator (cf. section 22.5) it is easy to obtain the number of types
that were specified with a certain TypeList. For example, the following
statement displays the value 3:
std::cout << TypeList<int, char, bool>::size << '\n';
However, it's illustrative to see how the number of types specified with a
TypeList could be determined if sizeof hadn't been available.
To obtain the number of types that were specified with a TypeList
the following algorithm is used:
TypeList contains no types, its size equals zero;
TypeList contains types, its size equals 1 plus the number
of types that follow its first type.
TypeList. In
executable C++ recursion could also be used in comparable situations. For
example recursion can be used to determine the length of an NTBS:
size_t c_length(char const *cp)
{
return *cp == 0 ? 0 : 1 + c_length(cp + 1);
}
While C++ functions usually use iteration rather than recursion, iteration is not available to template meta programming algorithms. In template meta programming repetition must be implemented using recursion. Furthermore, while C++ run-time code may use conditions to decide whether or not to start the next recursion template meta programming cannot do so. Template meta programming algorithms must resort to (partial) specializations. The specializations are used to select alternatives.
The number of types that are specified in a TypeList can be computed
using the following alternate implementation of TypeList, using a generic
struct declaration and two specialization for the empty and non-empty
TypeList (cf. the above description of the algorithm):
template <typename ...Types>
struct TypeList;
template <typename Head, typename ...Tail>
struct TypeList<Head, Tail...>
{
enum { size = 1 + TypeList<Tail...>::size };
};
template <>
struct TypeList<>
{
enum { size = 0 };
};
TypeList, an algorithm is used that either defines
`index' as -1 (if SearchType is not an element of the TypeList ) or it
defines `index' as the index of the first occurrence of SearchType in
the TypeList. The following algorithm is used:
TypeList is empty, `index' is -1;
TypeList's first element equals SearchType, `index' is 0;
TypeList's tail results in
`index' == -1;
TypeList's tail) index is
set to 1 + the index obtained when searching for SearchType in the
TypeList's tail.
ListSearch expecting a parameter pack:
template <typename ...Types>
struct ListSearch
{
ListSearch(ListSearch const &) = delete;
};
Specializations handle the alternatives mentioned with the algorithm:
TypeList is empty, `index' is -1:
template <typename SearchType>
struct ListSearch<SearchType, TypeList<>>
{
ListSearch(ListSearch const &) = delete;
enum { index = -1 };
};
TypeList's head equals SearchType, `index'
is 0. Note that SearchType is explicitly mentioned as the
TypeList's first element:
template <typename SearchType, typename ...Tail>
struct ListSearch<SearchType, TypeList<SearchType, Tail...>>
{
ListSearch(ListSearch const &) = delete;
enum { index = 0 };
};
TypeList's tail. The index
value returned by this search is stored in a tmp enum value,
which is then used to determine index's value.
template <typename SearchType, typename Head, typename ...Tail>
struct ListSearch<SearchType, TypeList<Head, Tail...> >
{
ListSearch(ListSearch const &) = delete;
enum {tmp = ListSearch<SearchType, TypeList<Tail...>>::index};
enum {index = tmp == -1 ? -1 : 1 + tmp};
};
ListSearch can be used:
std::cout <<
ListSearch<char, TypeList<int, char, bool>>::index << "\n" <<
ListSearch<float, TypeList<int, char, bool>>::index << "\n";
TypeList is retrieving the type given its index. This inverse operation is
the topic of this section.
The algorithm is implemented using a struct TypeAt. TypeAt specifies a
using-declaration to define the type matching a given index. But the index
might be out of bounds. In that case we have several options:
Null) that should not be used as a
type in the TypeList. This type is going to be returned when the index is
out of bounds. Using this local type as one of the types in a TypeList is
considered an error as its would conflict with the special meaning of Null
as the type returned at an invalid index.Null from being returned by TypeAt a static_assert
is used to catch the Null type when it is encountered while evaluating
TypeAt;
TypeAt may define an enum value validIndex set to
true if the index was valid and set to false if not.
TypeAt works:
TypeAt,
expecting an index and a TypeList:
template <size_t index, typename Typelist>
struct TypeAt;
static_assert ends the compilation
template <size_t index>
struct TypeAt<index, TypeList<>>
{
static_assert(index < 0, "TypeAt index out of bounds");
using Type = TypeAt;
};
Type as the first type in
the TypeList:
template <typename Head, typename ...Tail>
struct TypeAt<0, TypeList<Head, Tail...>>
{
using Type = Head;
};
Type is defined as Type defined by TypeAt<index
- 1> operating on the TypeList's tail:
template <size_t index, typename Head, typename ...Tail>
struct TypeAt<index, TypeList<Head, Tail...>>
{
using Type = typename TypeAt<index - 1, TypeList<Tail...>>::Type;
};
typeAt can be used. Uncommenting the first variable
definition causes a TypeAt index out of bounds compilation error:
using list3 = TypeList<int, char, bool>;
// TypeAt<3, list3>::Type invalid;
TypeAt<0, list3>::Type intVariable = 13;
TypeAt<2, list3>::Type boolVariable = true;
cout << "The size of the first type is " <<
sizeof(TypeAt<0, list3>::Type) << ", "
"the size of the third type is " <<
sizeof(TypeAt<2, list3>::Type) << "\n";
if (typeid(TypeAt<1, list3>::Type) == typeid(char))
cout << "The typelist's 2nd type is char\n";
if (typeid(TypeAt<2, list3>::Type) != typeid(char))
cout << "The typelist's 3nd type is not char\n";
TypeList is easy and doesn't require
recursive template meta programs. Two variadic template structs Append and
Prefix and two specializations are all it takes.
Here are the declarations of the two variadic template structs:
template <typename ...Types>
struct Append;
template <typename ...Types>
struct Prefix;
To append or prefix a new type to a typelist, specializations expect a
typelist and a type to add. Then, they simply define a new TypeList also
including the new type. The Append specialization shows that a template
pack does not have to be used as the first argument when defining another
variadic template type:
template <typename NewType, typename ...Types>
struct Append<TypeList<Types...>, NewType>
{
using List = TypeList<Types..., NewType>;
};
template <typename NewType, typename ...Types>
struct Prefix<NewType, TypeList<Types...>>
{
using List = TypeList<NewType, Types...>;
};
TypeList. Again, there are
several possibilities, each resulting in a different algorithm.
TypeList;
TypeList;
TypeList.
TypeList, keeping each type only once.
TypeList. Which ones are eventually implemented depends of course on
the circumstances. As template meta programming is very powerful most if not
all algorithms can probably be implemented. As an illustration of how to erase
types from a TypeList the above-mentioned algorithms are now developed in
the upcoming subsections.
EraseType from a TypeList
a recursive algorithm is used once again. The template meta program uses a
generic Erase struct and several specializations. The specializations
define a type List containing the resulting TypeList after the
erasure. Here is the algorithm:
Erase expecting the type to erase and a TypeList:
template <typename EraseType, typename TypeList>
struct Erase;
TypeList results:
template <typename EraseType>
struct Erase<EraseType, TypeList<>>
{
using List = TypeList<>;
};
TypeList's head matches the type to erase, then List
becomes a TypeList containing the original TypeList's tail
types:
template <typename EraseType, typename ...Tail>
struct Erase<EraseType, TypeList<EraseType, Tail...>>
{
using List = TypeList<Tail...>;
};
TypeList's tail. This results in a TypeList to which the
orginal TypeList's head must be prefixed. The TypeList
returned by the prefix operation is then returned as Erase::List:
template <typename EraseType, typename Head, typename ...Tail>
struct Erase<EraseType, TypeList<Head, Tail...>>
{
using List = typename
Prefix<Head,
typename Erase<EraseType, TypeList<Tail...>>::List
>::List;
};
Erase can be used:
cout <<
Erase<int, TypeList<char, double, int>>::List::size << '\n' <<
Erase<char, TypeList<int>>::List::size << '\n' <<
Erase<int, TypeList<int>>::List::size << '\n' <<
Erase<int, TypeList<>>::List::size << "\n";
TypeList by its index we again use a
recursive template meta program. EraseIdx expects a size_t index value
and a TypeList from which its idxth (0-based) type must be
erased. EraseIdx defines the type List containing the resulting
TypeList. Here is the algorithm:
EraseIdx expecting the index of the type to erase and a TypeList:
template <size_t idx, typename TypeList>
struct EraseIdx;
TypeList results:
template <size_t idx>
struct EraseIdx<idx, TypeList<>>
{
using List = TypeList<>;
};
idx becomes 0. At that point
the TypeList's first type is ignored and List is initialized
to a TypeList containing the types in the orginal TypeList's
tail:
template <typename EraseType, typename ...Tail>
struct EraseIdx<0, TypeList<EraseType, Tail...>>
{
using List = TypeList<Tail...>;
};
EraseIdx is applied to the TypeList's
tail, providing it with a decremented value of idx. To the
resulting TypeList the orginal TypeList's head is
prefixed. The TypeList returned by the prefix operation is then
returned as EraseIdx::List:
template <size_t idx, typename Head, typename ...Tail>
struct EraseIdx<idx, TypeList<Head, Tail...>>
{
using List = typename Prefix<
Head,
typename EraseIdx<idx - 1, TypeList<Tail...>>::List
>::List;
};
EraseIdx can be used:
if
(
typeid(TypeAt<2,
EraseIdx<1,
TypeList<int, char, size_t, double, int>>::List
>::Type
)
== typeid(double)
)
cout << "the third type is now a double\n";
EraseType from a TypeList can easily be accomplished
by applying the erasure procedure not only to the head of the TypeList but
also to the TypeList's tail.
Here is the algorithm, described in a slightly different order than
Erase's algorithm:
TypeList is empty, there's nothing to erase, and an empty
TypeList results. This is exactly what we do with Erase, so we
can use inheritance to prevent us from having to duplicate elements of
a template meta program:
template <size_t idx>
struct EraseIdx<idx, TypeList<>>
{
using List = TypeList<>;
};
EraseAll expecting the type to erase and a TypeList that is
derived from Erase, thus already offering the empty TypeList
handling specialization:
template <typename EraseType, typename TypeList>
struct EraseAll: public Erase<EraseType, TypeList>
{};
TypeList's head matches EraseType EraseAll is also
applied to the TypeList's tail, thus removing all occurrences of
EraseType from TypeList:
template <typename EraseType, typename ...Tail>
struct EraseAll<EraseType, TypeList<EraseType, Tail...>>
{
using List = typename EraseAll<EraseType, TypeList<Tail...>>::List;
};
TypeList's head does not match
EraseType) EraseAll is applied to the TypeList's tail.
The returned TypeList consists of the original TypeList's
initial type and the types of the TypeList returned by the
recursive EraseAll call:
template <typename EraseType, typename Head, typename ...Tail>
struct EraseAll<EraseType, TypeList<Head, Tail...>>
{
using List = typename Prefix<
Head,
typename EraseAll<EraseType, TypeList<Tail...>>::List
>::List;
};
EraseAll can be used:
cout <<
"After erasing size_t from "
"TypeList<char, int, size_t, double, size_t>\n"
"it contains " <<
EraseAll<size_t,
TypeList<char, int, size_t, double, size_t>
>::List::size << " types\n";
TypeList all the TypeList's first
elements must be erased from the TypeList's tail, applying the procedure
recursively to the TypeList's tail. The algorithm, outlined below, merely
expects a TypeList:
EraseDup struct template is
declared. EraseDup structures define a type List representing the
TypeList that they generate. EraseDup calls expect a TypeList as
their template type parameters:
template <typename TypeList>
struct EraseDup;
TypeList is empty it can be returned empty and we're done:
template <>
struct EraseDup<TypeList<>>
{
using List = TypeList<>;
};
EraseDup is first applied to the original TypeList's
tail. By definition this results in a TypeList from which all
duplicates have been removed;
TypeList returned by the previous step might contain the
original TypeList's initial type. If so, it is removed by applying
Erase on the returned TypeList, specifying the original TypeList's
initial type as the type to remove;
TypeList consists of the original TypeList's
initial type to which the types of the TypeList produced by the previous
step are appended.
template <typename Head, typename ...Tail>
struct EraseDup<TypeList<Head, Tail...>>
{
using UniqueTail = typename EraseDup<TypeList<Tail...>>::List;
using NewTail = typename Erase<Head, UniqueTail>::List;
using List = typename Prefix<Head, NewTail>::List;
};
EraseDup can be used:
cout <<
"After erasing duplicates from "
"TypeList<double, char, int, size_t, int, double, size_t>\n"
"it contains " <<
EraseDup<
TypeList<double, char, int, size_t, int, double, size_t>
>::List::size << " types\n";
But there's more to typelist than a mere intellectual challenge. In the final sections of this chapter the following topics are covered:
Multi
is now developed. The class template Multi creates a new class from a
template template parameter Policy defining the data storage policy and a
series of types from which Multi is eventually derived. It does so by
passing its template parameters to its base class MultiBase that in turn
creates a final class inheritance tree. Since we don't know how many types are
going to be used Multi is defined as a variadic class template using a
template pack ...Types.
In fact, the types that are specified with Multi aren't that
interesting. They primarily serve to `seed' the class Policy. Therefore,
rather than forwarding Multi's types to MultiBase they are passed to
Policy and the sequence of Policy<Type> types is then forwarded to
MultiBase. Multi's constructor expects initialization values for its
various Policy<Type>s which are perfectly forwarded to MultiBase.
The class Multi (implementing its constructor in-class to save some
space) shows how a
template pack can be wrapped into a policy. Here is Multi's definition:
template <template <typename> class Policy, typename ...Types>
struct Multi: public MultiBase<0, Policy<Types>...>
{
using PlainTypes = TypeList<Types...>;
using Base = MultiBase<0, Policy<Types>...>;
enum { size = PlainTypes::size };
Multi(Policy<Types> &&...types)
:
MultiBase<0, Policy<Types>...>(
std::forward<Policy<Types>>(types)...)
{}
};
Unfortunately, the design as described contains some flaws.
Policy template template parameter is defined as
template <typename> class Policy it can only accept policies expecting one
type argument. Contrary to this, std::vector is a template expecting two
template arguments, the second one defining the allocation scheme used by
std::vector. This allocation scheme is hardly ever changed, and most
applications merely define objects of types like vector<int>,
vector<string> etc.. Template template parameters must, however, be specified
with the correct number and types of required template parameters so
vector can't be specified as a policy for Multi. This can be solved by
wrapping a more complex template in a simpler wrapper template, like so:
template <class Type>
struct Vector: public std::vector<Type>
{
Vector(std::initializer_list<Type> iniValues)
:
std::vector<Type>(iniValues)
{}
};
Now Vector provides std::vector's second parameter using its
default template argument. Alternatively, a template using declaration
could be used.
TypeList contains two types like int and double
and the policy class is Vector, then the MultiBase class
eventually inherits from vector<int> and vector<double>. But if the
TypeList contains identical types, like two int type specifications
MultiBase would inherit from two vector<int> classes. Classes
cannot be derived from identical base classes as that would make it impossible
to distinguish among their members. Regarding this, Alexandrescu (2001)
writes (p.67):
There is one major source of annoyance...: you cannot use it when you have duplicate types in yourTypeList.
.... There is no easy way to solve the ambiguity, [as the eventually derived class/FBB] ends up inheriting [the same base class/FBB] twice.
IntType. The class template UWrap has two template parameters: one
non-type parameter idx and one type parameter. By ensuring that each
UWrap definition uses a unique idx value unique class types are
created. These unique class types are then used as base classes of the derived
class MultiBase:
template <size_t nr, typename Type>
struct UWrap: public Type
{
UWrap(Type const &type)
:
Type(type)
{}
};
Using UWrap it's easy to distinguish, e.g., two vector<int>
classes: UWrap<0, vector<int>> could refer to the first vector<int>,
UWrap<1, vector<int>> to the second vector.
Uniqueness of the various UWrap types is assured by the class
template MultiBase as discussed in the next section.
It must also be possible to initialize a Multi class object. Its
constructor therefore expects the initialization values for all its Policy
values. So if a Multi is defined for Vector, int, string then its
constructor can receive the matching initialization values. E.g.,
Multi<Vector, int, string> mvis({1, 2, 3}, {"one", "two", "three"});
MultiBase is Multi's base class. It
defines a class that, eventually, is derived from the list of Policy
types that, in turn, were created by Multi using any additional types that
were passed to it.
MultiBase itself has no concept of a Policy. To MultiBase the
world appears to consist of a simple template pack whose types are used to
define a class from. In addition to the PolicyTypes template pack,
MultiBase also defines a size_t nr non-type parameter that is used to
create unique UWrap types. Here is MultiBase's generic class
declaration:
template <size_t nr, typename ...PolicyTypes>
struct MultiBase;
Two specializations handle all possible MultiBase invocations. One
specialization is a recursive template. This template handles the first type
of MultiBase's template parameter pack and recursively uses itself to
handle the remaining types. The second specialization is invoked once the
template parameter pack is exhausted and does nothing. Here is the definition
of the latter specialization:
template <size_t nr>
struct MultiBase<nr>
{};
The recursively defined specialization is the interesting one. It performs the following tasks:
UWrap type. The uniqueness is
guaranteed by using MultiBase's nr parameter when defining
UWrap. In addition to nr the UWrap class receives the first type
of the template parameter pack made available to MultiBase;
MultiBase type is defined using as its first template argument an
incremented nr value (thus ensuring the uniqueness of the UWrap types
defined by recursive MultiWrap types). Its second template argument is the
tail of the template parameter pack made available to MultiBase
MultiBase class
hierarchy is provided in figure 29.

MultiBase's constructor simply receives the initialization values that
were (originally) passed to the Multi object. Perfect forwarding is used
to accomplish this. MultiBase's constructor passes its first parameter
value to its UWrap base class, also using perfect forwarding.
MultiBase's recursive definition is:
template <size_t nr, typename PolicyT1, typename ...PolicyTypes>
struct MultiBase<nr, PolicyT1, PolicyTypes...> :
public UWrap<nr, PolicyT1>,
public MultiBase<nr + 1, PolicyTypes...>
{
using Type = PolicyT1;
using Base = MultiBase<nr + 1, PolicyTypes...>;
MultiBase(PolicyT1 && policyt1, PolicyTypes &&...policytypes)
:
UWrap<nr, PolicyT1>(std::forward<PolicyT1>(policyt1)),
MultiBase<nr + 1, PolicyTypes...>(
std::forward<PolicyTypes>(policytypes)...)
{}
};
Multi class template defines PlainTypes as the TypeList
holding all the types of its parameter pack. Each MultiBase derived from a
UWrap type also defines a type Type representing the policy type that
was used to define the UWrap type and a type Base representing the
type of its nested MultiBase class.
These three type definitions allow us to access the types from which the
Multi object was created as well as the values of those types.
The class template typeAt, is a pure template meta program class template
(it has no run-time executable code). It expects a size_t idx template
argument specifying the index of the policy type in a Multi type object as
well as a Multi class type. It defines the type Type as the Type
defined by Multi's MultiBase<idx, ...> base class. Example:
typeAt<0, Multi<Vector, int, double>>::Type // Type is vector<int>
The class template typeAt defines (and uses) a nested class template
PolType doing all the work. PolType's generic definition specifies two
template parameters: an index used to specify the index of the requested type
and a typename initialized by a MultiBase type argument. PolType's
recursive definition recursively reduces its index non-type parameter,
passing the next base class in MultiBase's inheritance tree to the
recursive call. As PolType eventually defines the type Type to be the
requested policy type the recursive definition defines its Type as the
type defined by the recursive call. The final (non-recursive) specialization
defines the initial policy type of the MultiBase type as Type. Here is
typeAt's definition:
template <size_t index, typename Multi>
class typeAt
{
template <size_t idx, typename MultiBase>
struct PolType;
template <size_t idx,
size_t nr, typename PolicyT1, typename ...PolicyTypes>
struct PolType<idx, MultiBase<nr, PolicyT1, PolicyTypes...>>
{
using Type = typename PolType< idx - 1, MultiBase<nr + 1,
PolicyTypes...> >::Type;
};
template <size_t nr, typename PolicyT1, typename ...PolicyTypes>
struct PolType<0, MultiBase<nr, PolicyT1, PolicyTypes...>>
{
using Type = PolicyT1;
};
public:
typeAt(typeAt const &) = delete;
using Type = typename PolType<index, typename Multi::Base>::Type;
};
The types specified by Multi's parameter pack can also be retrieved using
a second helper class template: plainTypeAt. Example:
plainTypeAt<0, Multi<Vector, int, double>>::Type // Type is int
The class template plainTypeAt uses a comparable (but simpler)
implementation than typeAt. It is also a pure template meta program class
template defining a nested class template At. At is implemented like
typeAt but it visits the types of the original template pack that was
passed to Multi, and made available by Multi as its PlainTypes
type. Here is plainTypeAt's definition:
template <size_t index, typename Multi>
class plainTypeAt
{
template <size_t idx, typename List>
struct At;
template <size_t idx, typename Head, typename ...Tail>
struct At<idx, TypeList<Head, Tail...>>
{
using Type = typename At<idx - 1, TypeList<Tail...>>::Type;
};
template <typename Head, typename ...Tail>
struct At<0, TypeList<Head, Tail...>>
{
using Type = Head;
};
public:
plainTypeAt(plainTypeAt const &) = delete;
using Type = typename At<index, typename Multi::PlainTypes>::Type;
};
Arguably the neatest support template is get. This is a function template
defining size_t idx as its first template parameter and typename Multi
as its second template parameter. The function template get defines one
function parameter: a reference to a Multi, so it can deduce Multi's
type by itself. Knowing that it's a Multi, we reason that it is also a
UWrap<nr, PolicyType> and therefore also a PolicyType, as the latter
class is defined as a base class of UWrap.
Since class type objects can initialize references to their base classes the
PolicyType & can be initialized by an appropriate UWrap reference,
which in turn can be initialized by a Multi object. Since we can
determine PolicyType using TypeAt (note that evaluating typename
typeAt<idx, Multi>::Type is a purely compile-time matter), the get
function can very well be implemented inline by a single return
statement:
template <size_t idx, typename Multi>
inline typename typeAt<idx, Multi>::Type &get(Multi &multi)
{
return static_cast<
UWrap<idx, typename typeAt<idx, Multi>::Type> &>(multi);
}
The intermediate UWrap cast is required to disambiguate between
identical policy types (like two vector<int> types). As UWrap is
uniquely determined by its nr template argument and this is the number
argument that is passed to get ambiguities can easily be prevented.
Multi and its support templates have been developed, how can a
Multi be used?
A word of warning is in place. To reduce the size of the developed classes
they were designed in a minimalist way. For example, the get function
template cannot be used with Multi const objects and there is no default,
or move constructor available for Multi types. Multi was designed to
illustrate some of the possibilities of template meta programming and
hopefully Multi's implementation served that purpose well. But can it be
used? If so, how?
This section provides some annotated examples. They may be concatenated to
define a series of statements that could be placed in a main function's
body, which would result in a working program.
Policy could be defined:
template <typename Type>
struct Policy
{
Type d_type;
Policy(Type &&type)
:
d_type(std::forward<Type>(type))
{}
};
Policy defines a data member and it can be used to define Multi
objects:
Multi<Policy, string> ms{ Policy<string>{ "hello" } };
Multi<Policy, string, string> ms2s{ Policy<string>{ "hello" },
Policy<string>{ "world" } };
using MPSI = Multi<Policy, string, int>;
MPSI mpsi{ string{ "hello" }, 4 };
Multi class or object
either use the ::size enum value (using the Multi class) or the
.size member (using the Multi object):
cout << "There are " << MPSI::size << " types in MPSI\n"
"There are " << mpsi.size << " types in mpsi\n";
plainTypeAt:
plainTypeAt<0, MPSI>::Type sx = "String type";
plainTypeAt<1, MPSI>::Type ix = 12;
cout << static_cast<Policy<string> &>(mpsi).d_type << '\n' <<
static_cast<Policy<int> &>(mpsi).d_type << '\n';
Policy<Type> types. In that case get still works fine:
using MPII = Multi<Policy, int, int>;
MPII mpii{ 4, 18 };
cout << get<0>(mpii).d_type << ' ' << get<1>(mpii).d_type << '\n';
std::vector in a Vector:
using MVID = Multi<Vector, int, double>;
MVID mi{ {1, 2, 3}, {1.2, 3.4, 5.6, 7.8} };
Multi type:
typeAt<0, Multi<Vector, int>>::Type vi = {1, 2, 3};
Vector is a std::vector, the reference
returned by get support index operators that can be used as left hand side
or right hand side operands:
cout << get<0>(mi)[2] << '\n';
get<1>(mi)[3] = get<0>(mi)[0];
cout << get<1>(mi)[3] << '\n';
Assume we are processing std::vector objects. Vectors may be assigned to
each other, but that's about it. We've seen (cf. section 12.4.2) that its
member functions tend to operate on the current vector, but arithmetic
operations like addition, subtraction, multiplication and the like cannot
be applied to pairs of vectors.
Implementing the, e.g., addition operator for vectors is not difficult. If
VecType is our vector type, then implementing free functions like
VecType &&operator+(VecType const &lhs, VecType const &rhs) and
VecType &&operator+(VecType &&lhs, VecType const &rhs)
performing the additions is a simple exercise (cf. chapter
11).
Now consider an expression like one + two + three + four. It takes four
steps to compute this sum: first, tmp = one is computed, creating the
eventual return value. The vector tmp becomes the eventual return
value. Once it is available tmp += two is computed, followed by tmp +=
three, and finally by tmp += four (of course
we shouldn't implement std::vector::operator+= as the std namespace is
off-limits to us, and we shouldn't derive a class from std::vector
offering operator+= according to Liskov's Substitution Principle
(cf. section 14.7), but we could get around that.
Here we simply assume operator+= is available).
Here's how we might implement operator+= for VecType:
VecType &VecType::operator+=(VecType const &rhs)
{
for (size_t idx = 0, end = size(); idx != end; ++idx)
(*this)[idx] += rhs[idx];
return *this;
}
Consider this implementation: once we add VecType objects and such
objects have N elements then we have to perform 2 * N index
evaluations. When adding k VecType objects this adds up to 2 * N * k
index expression evaluations (as eventually we also have to assign the
elements of the resulting temporary object to the destination object): lots
of index expression evaluations.
If instead we could manage to perform the evaluations `row by row', we
would only have to access each vector element only once (which in particular
applies to the temporary object). In that case, when adding k objects,
assigning the sums of their respective elements to a destination vector we
have to compute N * (k + 1) index expressions (`k' for each of the
vectors, `1' for the destination vector).
For k == 1 the two methods are equally efficient in terms of index
computations. But that's not addition, that is assignment. So when adding any
number of vectors, assigning their sum to a destination vector using expression
templates
is more efficient than the ordinary implementation of the addition
operator. We'll have a look at the design and implementation of expression
templates in the coming sections.
one + two + three + four, where the objects are vectors having n
elements, then if we have k vectors we have to perform a total of k * 2
* n index evaluations.
Expression templates allow us to avoid many of these evaluations. When using expression templates these templates may access the vectors, but their elements are not accessed during addition operations.
Assuming our expression template is named ET, and we want to add one + two
+ three, then the first + operator merely creates ET(one, two). Note
that no addition is actually performed, ET merely stores (constant)
references to one (becoming ET's lhs data member) and two
(becoming ET's rhs data member). In general, ET stores references to
the two arguments that are passed to its constructor.
At the next addition operator another ET is created. Its constructor
arguments are, respectively, the ET object that has just been constructed
for one and two, and the vector three. Again, no addition is
performed by the ET objects.
This algorithm easily generalizes to any number of vectors. Parentheses can
also be used. E.g., (one + two) + (three + four) results in
ET(ET(one, two), ET(three, four))
Presumably, at some point we want to obtain the sum of the vectors. For this
the expression template is provided with a conversion operator, converting the
ET object to a vector, or maybe an assignment operator doing the same.
The conversion operator looks like this:
operator ET::VecType() const
{
VecType retVal;
retVal.reserve(size());
for (size_t ix = 0, end = size(); ix != end; ++ix)
new(&retVal[ix]) value_type((*this)[ix]);
return retVal;
}
Placement new is used for efficiency reasons: there's no need to
initialize retVal with default values first. The really interesting part,
however, is hidden behind the (*this)[idx] expression: at this point the
real addition takes place.
ET's index operator simply adds the values returned by the
corresponding index expressions of its lhs and rhs data members. If a
data member refers to a vector then the corresponding vector element is used,
adding it to the other data member's value. If a data member itself refers to
an ET object, then that nested ET object's index operator performs the
same addition on its own data members, returning their sum. So, an expression
like (*this)[0] returns first[0] + second[0] + third[0], and the
computed sum is then stored in retVal[0] using placement new.
In this case the required number of index expression evaluations are n
* k (for the n elements of the k vectors) plus n (for the n elements of
retVal, adding up to (k + 1) * n).
Since (k + 1) * n < 2 * k * n for k > 1 expression templates evaluate
the requested addition more efficiently than the traditional implementation of
operator+. An additional benefit of using expression templates is that
they do not create additional temporary vector objects when parenthesized
expressions are used.
using IntVect = std::vector<int> to illustrate
the construction of an expression template.
Starting point is a simple main function, in which several IntVect
objects are added. E.g.,
int main()
{
IntVect one;
IntVect two;
IntVect three;
IntVect four;
// ... assume the IntVects somehow receive values
four = one + two + three + four;
}
At this point the code does not suggest that expression templates are
going to be used. However, operator+'s implementation is special: it's a
template merely returning an object constructed by operator+:
template<typename LHS, typename RHS>
BinExpr<LHS, RHS, plus> operator+(LHS const &lhs, RHS const &rhs)
{
return BinExpr<LHS, RHS, plus>{ lhs, rhs };
}
Our expression template is called BinExpr. It has three template type
parameters: two object types and a template template parameter performing the
requested operation. Its declaration looks like this:
template<typename LHS, typename RHS, template<typename> class Operation>
struct BinExpr;
Since LHS and RHS can either be the data type that is processed by
the expression template, or a BinExpr two different typenames are
required. Operation is the operation that is performed by the expression
template. By using a template template parameter we can use BinExpr to
perform any operation we want, not just addition. Predefined function
templates like std::plus can be used for the standard arithmetic
operators; for other operators we can define our own function templates.
BinExpr's constructor initializes constant references to lhs and
rhs. Its in-class implementation is
BinExpr(LHS const &lhs, RHS const &rhs)
:
d_lhs(lhs),
d_rhs(rhs)
{}
To retrieve the resulting IntVect a conversion operator is defined. We
already encountered its implementation (in the previous section). Here is it,
as an in-class implemented BinExpr member:
operator ObjType() const
{
ObjType retVal;
retVal.reserve(size());
for (size_t idx = 0, end = size(); idx != end; ++idx)
new(&retVal[idx]) value_type((*this)[idx]);
return retVal;
}
We return to the type ObjType below. At this point it can be
considered an IntVect. The member size() simply returns
d_lhs.size(): in any sequence of IntVect additions LHS eventually
is an IntVect, and so every BinExpr defines a valid size() like
so:
size_t size() const
{
return d_lhs.size();
}
The only remaining member to implement is operator[]. Since it
receives an index, it only needs to perform the requested operation on the
corresponding index elements of its d_lhs and d_rhs data members. The
beauty of expression templates is that if either one itself is a BinExpr
that expression template in turn calls its operator[], eventually
performing the requested operation on all corresponding elements of all
IntVect objects. Here is its implementation:
value_type operator[](size_t ix) const
{
static Operation<value_type> operation;
return operation(d_lhs[ix], d_rhs[ix]);
}
This implementation uses another type: value_type which is the
type of the elements of the vector type that is processed by the expression
template. Like ObjType before, its definition is covered below. The static
data member operation simply is an instantiation of the Operation type
that is specified when constructing an ExprType object.
In the next section we take a closer look at ObjType and value_type.
BinExpr expression template needs to be aware of two types before it
can instantiate objects. First, ObjType must be known, as this is the
type of object that is handled by the expression template. ObjType objects
contain values, and we require that the type of these values can be determined
as ObjType::value_type. E.g., for our IntVect data type value_type
is int.
In expressions like one + two + three, the BinExpr expression template
receives two IntVect objects. This is always true: the BinExpr that is
first constructed receives two IntVect objects. In this case ObjType
is simply LHS, and ObjType::value_type is also available: either
value_type is already defined by LHS or BinExpr requires that
it defines type value_type.
Since arguments to BinExpr objects are not always of the basic
ObjType type (BinExpr objects at the next nesting level receive at
least one BinExpr argument) we need a way to determine ObjType from a
BinExpr. For this we use a trait class. The
trait class BasicType receives a typename template argument, and equates
its type ObjType to the received template type argument:
template<typename Type>
struct BasicType
{
using ObjType = Type ;
};
A specialization handles the case where Type in fact is a BinExpr:
template<typename LHS, typename RHS, template<typename> class Operation>
template<typename LHS, typename RHS, template<typename> class Operation>
struct BasicType<BinExpr<LHS, RHS, Operation>>
{
using ObjType = BinExpr<LHS, RHS, Operation>::ObjType ;
};
Since BinExpr requires that ObjType::value_type is a defined
type, value_type has automatically been taken care of.
As BinExpr refers to BasicType and BasicType refers to
BinExpr somewhere we must provide a forward declaration. As BinExpr's
declaration has already been provided, we start with that declaration,
resulting in:
BinExpr's declaration
BasicType's definition
BasicType's specialization (for BinExpr)
template<typename LHS, typename RHS, template<typename> class Operation>
class BinExpr
{
LHS const &d_lhs;
RHS const &d_rhs;
public:
using DataType = BasicType<RHS>::DataType ;
using type = DataType::value_type value_;
// all BinExpr member functions
};
C++ is a strongly typed language: a function add(int lhs, int rhs)
doesn't accept std::string arguments, even though the actual operations
(lhs + rhs) are identical for ints and strings.
Templates were introduced so we could design recipes for the compiler, allowing it to construct type-safe overloaded versions of functions and classes while keeping their type-safety.
A basic addition function template adding two values looks like this:
template <typename Type>
Type add(Type const &lhs, Type const &rhs)
{
return lhs + rhs;
}
When this function template is called with arguments of types that do not
support operator+ then the compiler notices this, and it will generate an
error. E.g., when calling
add(std::cerr, std::cout);the
g++ compiler produces some 140 lines of error messages. It notices
that there's no operator+ for std::ostream objects, and then tells us
what else we might have done (like adding two ints), and where the
construction of the add function that should accept std::ostream
arguments went wrong. In fact, 140 lines of error messages is rather benign.
Getting several hundreds of lines is quite common, and sometimes the
location of the error isn't mentioned at the top but somewhere near the end of
the error message output.
The C++20 standard introduced concepts allowing us to specify
requirements for template types. When applying an appropriate concept to
the definition of the add function template the compiler immediately
pinpoints the error, telling us where and why the error occurred in some 15
instead of 140 lines of error messages.
The reduction of the number of lines of error messages by itself is a boon. But the fact that concepts allow us to consciously develop our templates, realizing what the precise requirements are for their use, is at least as important: it improves the template's documentation, and thus our understanding of templates.
Concepts may be considered the template's answer to the philosphy that lies
behind a strongly typed language. By applying concepts to templates we can
specify type-requirements rather than using the traditional `shotgun
empiricism' approach where templates are bluntly used, knowing that the
compiler will complain if things are incorrect. In that sense concepts provide
type definitions of types. Concepts have names and can (among other) be used
in template headers where the concept names replace the traditional
typename keywords.
As an opening illustration, assume that a concept Addable exists
specifying that operator+ must have been defined for the template's
type. The above function template add can now be formulated as:
template<Addable Type>
Type add(Type const &lhs, Type const &rhs)
{
return lhs + rhs;
}
From now on every type that is actually passed to add must be
satisfy the Addable requirements. Here are two expressions
using add:
add("first"s, "second"s); // (1)
add(map<int, int>{}, map<int, int>{}); // (2)
Expression (1) flawlessly compiles as string objects can be added;
expression (2) fails with the compiler reporting something like
error: use of function `Type add(const Type&, const Type&)
[with Type = std::unordered_map<int, int>]' with unsatisfied constraints
add(unordered_map<int, int>{}, unordered_map<int, int>{});
note: constraints not satisfied
Type add(const Type&, const Type&)
...
note: the required expression `(lh + rh)' is invalid
The error message's final `note' clearly states the cause of the problem: you can't add maps.
The difference between the compiler's report using concepts and not using
concepts again is impressive. When using the traditional typename Type
specification in the template header the compiler produces some 17 kB of error
messages, spread out over more than 200 lines.
In the following sections we cover how concepts are defined, what kind of requirements can be formulated, and how they can be used in practice.
Constraint' or
`Concept', but use names like `Addable' and `HasValueType'.
Concepts are templates. They start with a template header (the template headers shown in the examples define a single template type parameter, but multiple template parameters are also used).
In the previous section we used the concept Addable. Here is how it can
be defined:
template <typename Type>
concept Addable =
requires(Type lh, Type rh)
{
lh + rh;
};
The concept's template header is followed by the keyword concept, the
concept's name, and the assignment operator. Following the assignment operator
requirement specifications are provided.
Semicolons end concept definitions. This concept uses a
simple requirement (cf. section 23.13.2.1) indicating that
operator+ must have been defined for Addable templates' types.
Requirements come in many forms. A very simple form consists of just a
bool value, which is sometimes useful when developing a concept. Such a
concept looks like this:
template <typename Type>
concept IsTrue =
true;
But in most situations requires specifications are used. They resemble
function definitions having parameter lists optionally defining variables of
the types that specified in the concept's template header and compound
statements specifying requirements.
Concepts are never instantiated. They are used compile-time to verify that
template types satisfy the imposed requirements. Thus there's no need
to use refererences in parameter lists of requires specifications. The
concept Addable simply uses
requires(Type lh, Type rh)
and there's no need to specify
requires(Type const &lh, Type const &rh)(That is, usually there is no need for this. In section 23.13.2.4 we encounter a situation where a more specific parameter definition might be appropriate.)
Here are two examples of templates using concept Addable. The first
example uses Addable instead of typename when specifying the template
header, the second example appends the concept specification to the template
header itself:
template<Addable Type>
Type add2(Type const &x, Type const &y)
{
return x + y;
}
template<typename Type>
requires Addable<Type>
Type add(Type const &x, Type const &y)
{
return x + y;
}
Template declarations using concepts are specified accordingly. Simply replace the function template's body by a semicolon.
Concepts may also be defined by extending or combining existing concepts. Nesting concepts is covered in section 23.13.2.4.
Although concepts are templates, they cannot be specialized. If a concept should recognize specializations then these specializations must be handled by the concepts' definitions. Section 23.13.2.3 for an illustration
requires declarations contain define constraints to apply to
template parameters. There are four types of requirements:
operator+);
value_type) which must be available when using
standard push_back functions;
Constraints must be compile-time verifiable.
When multiple constraints are specified, they must all be compile-time verifiable, and an actual type is only accepted by the compiler if all requirements could be satisfied.
requires specifications. When the requirements
refer to single variables single Type parameters suffice; when
requirements involve different types then the concept's template head declares
those different types and the requires parameter list will usually define
variables of those different types. The concept BasicMath specifies two
types, and uses four simple requirements to specify the four basic arithmetic
operations:
template <typename LhsType, typename RhsType>
concept BasicMath =
requires(LhsType lhs, RhsType rhs)
{
lhs + rhs; // addition must be available
lhs - rhs; // subtraction must be available
lhs * rhs; // multiplication must be available
lhs / rhs; // division must be available
};
Specifying constraints does not necessarily mean that the constraints as specified literally apply to run-time situations. To require the existence of the index operator the following simple requirement can be used:
template <typename Type>
concept HasIndex =
requires(Type tp)
{
tp[0];
};
template <HasIndex Type>
auto idx(Type const &obj, size_t idx)
{
return obj[idx];
}
Here the stand-in argument 0 is used to specify the index operator's
argument. The argument value used in the simple requirement really is a
stand-in. The following code fragment compiles, as string supports the
index operator. Athough argument 0 is used in the simple requirement
specification the argument 5 is in fact being used:
string str;
idx(str, 5);
Other than int index types can be specified analogously. Here is an
example showing how to define and use a concept HasStrIndex requiring the
availability of std::string arguments of index operators:
template <typename Type>
concept HasStrIndex =
requires(Type tp)
{
tp[std::string{}];
};
template <HasStrIndex Type>
auto value(Type &obj, std::string const &key)
{
return obj[key];
}
int main()
{
std::map<std::string, double> msd;
value(msd, "hi");
}
iterator (like
vector<int>::iterator) or value_type which is used when calling
std::push_back.
To specify that a sub-type must be available the concept's requires
specification needs no parameters, but can directly refer to the subtype. It's
also possible to combine type requirements with requirements that do
define a non-empty parameter list, and so the requires's parameter list
does not have to be empty. Here is a concept that specifies a plain type
requirement:
template <typename Type>
concept HasValueType =
requires()
{
typename Type::value_type;
};
and here's a concept that combines a simple requirement with a type
requirement:
template <typename Type>
concept Iteratable =
requires(Type tp)
{
typename Type::iterator;
tp.begin();
};
template <Iteratable Type>
auto iter(Type const &obj)
{
return obj.begin();
}
Calling iter with a string argument succeeds, calling it with a
queue argument results in two error notes: no Type::iterator and no
tp.begin().
Types specified in type requirements don't necessarily have to refer to
types. They may also specify be the names of nested classes or
enumerations defined by Type. When specifying enumerations they do not
have to be strongly typed.
C++20 standard
defines several concepts that can be used to specify such requirements (see
also section 23.13.3 below). Here is an example:
template <typename Type, typename ReturnType>
concept Return =
requires(Type par)
{
// par[..] must return a `ReturnType'
{ par[0] } -> std::same_as<ReturnType>;
};
This concept can now be used to specify requirements of template type parameters. E.g.,
template <typename Type, typename RetType>
requires Return<Type, RetType>
Ret fun(Type tp)
{
return tp[0];
}
Here arguments passed to fun must satify two requirements:
std::string values.
You may have noticed that the std::same_as concept receives only one
template type argument, which (as if by magic) compares it with the type
returned by the par[0] expression. When peeking at the available concepts
in section 23.13.3 you will see that several of those concepts in
fact define two template type parameters. When these concepts are used in
compound requirements then the compiler passes the deduced type of the
expression in the concept's compound statement (so that's the type of
par[0] in the above example) to the concept's first type, and passes the
explicitly specified type to the concept's second type.
Knowing this we can define our own concepts to use in compound
expressions. We may define our own same_as concept as follows, using a
separate class template SameTypes. SameTypes defines a
bool value `value' which is used to decide about the concept's
requirement. The class template SameTypes uses a specialization to handle
the situation where both types are equal. Note that concepts
themselves cannot be specialized:
template <typename Lhs, typename Rhs>
struct SameTypes // generic: any two types
{
static bool const value = false;
};
template <typename Lhs>
struct SameTypes<Lhs, Lhs> //specialization: equal types
{
static bool const value = true;
};
template<typename Compound, typename Specified>
concept Same = SameTypes::value;
Now the concept Same can be used instead of std::same_as by merely
specifying the required type:
template <typename Type, typename ReturnType>
concept Return =
requires(Type par)
{
// par[..] must return a `ReturnType'
{ par[0] } -> Same<ReturnType>;
};
Although in this case it isn't important which actual type is used as
argument for which concept type parameter, the compiler specifies the compound
expression's type as template argument for Same's Compound parameter
whereas ReturnType is used as template argument for Same's Specified
parameter.
Multiple type requirements can be specified by providing multiple compound requirements as in the following example:
template <typename Type>
concept MultiArgs =
requires(Type lhs, Type rhs)
{
{ lhs + rhs } -> std::same_as<Type>;
{ lhs += rhs } -> std::same_as<Type &>;
{ lhs.c_str() } -> std::same_as<char const *>;
};
If it is required that the compound operation doesn't throw exceptions then
noexcept can be written immediately following the compound requirement's
late return type arrow (->). The noexcept specification itself may
then optionally be followed by a type constraint.
Finally, the late return type specifications itself is optional, in which case the compound requirement acts like a simple requirement: it requires the existence of the expression that's specified in the compound statement. In this case: don't forget to add the semicolon following the closing parenthesis of the compound requirement:
template <typename Type>
concept Increment =
requires(Type par)
{
{ ++par };
// same as:
++par;
};
In chapter 18 iterators were introduced (section 18.2). Commonly five conceptually different iterator types are distinguished:

All iterator types support (in)equality checks and increment operators. Thus, at the basis of all iterators we find the requirements that iterators must be comparable and incrementable. Concepts covering those requirements are easily constructed (see also figure 30):
template <typename Type>
concept Comparable =
requires (Type lhs, Type rhs)
{
lhs == rhs;
lhs != rhs;
};
template <typename Type>
concept Incrementable =
requires (Type type)
{
++type;
type++;
};
Note that no type is specified following the lhs == rhs and lhs !=
rhs requirements, as those types are implied by their operators.
Two more concepts are defined: one allowing dereferencing pointers
returning constant references and one returning modifiable references. To
allow the compiler to verify those requirements we also implicitly require the
(commonly encountered) existence of typename Type::value_type:
template <typename Type>
concept Dereferenceable =
requires(Type type)
{
{ *type } -> std::same_as<typename Type::value_type &>;
};
template <typename Type>
concept ConstDereferenceable =
requires(Type type)
{
{ *type } -> std::same_as<typename Type::value_type const &>;
};
Not much of a hierarchy so far, but that changes now that we're about to define concepts for iterators.
An input iterator is an iterator that is comparable, incrementable and
const-dereferenceable. For each of these requirements concepts were defined
which can be combined using boolean operators when defining the concept
InIterator. Note that template type parameters of concepts must use
the typename keyword. Concepts'
template parameters cannot be constrained by
specifying them in terms of existing concepts (which is possible when
defining function and class templates).
Here is the definition of the concept InIterator. The function template
inFun (below the concept InIterator) illustrates how a
constrained template parameter type can be specified in template headers:
template <typename Type>
concept InIterator =
Comparable<Type> and Incrementable<Type> and
ConstDereferenceable<Type>;
template <InIterator Type>
void inFun(Type tp)
{}
The concept for output iterators (and its use, as in the function
template outFun) is defined analogously. This time requiring
dereferenceable types rather than const-dereferenceable types:
template <typename Type>
concept OutIterator =
Comparable<Type> and Incrementable<Type> and
Dereferenceable<Type>;
template <OutIterator Type>
void outFun(Type tp)
{}
For forward iterators the concept FwdIterator is defined. A forward
iterator combines the characteristics of input and output iterators, and we
may want to define a forward iterator by requiring the requirements of the
InIterator and OutIterator concepts.
However, there's a slight problem. The following class (struct) defines const and non-const dereference operators and may be therefore be passed to functions expecting input or output iterators:
struct Iterable
{
using value_type = int;
Iterable &operator++();
Iterable operator++(int);
int const &operator*() const;
int &operator*();
};
bool operator==(Iterable const &lh, Iterable const &rh);
bool operator!=(Iterable const &lh, Iterable const &rh);
int operator-(Iterable const &lh, Iterable const &rh);
But when a function template requires ConstDerefenceable arguments then
the compiler notices that the overloaded member int &operator*() doesn't
return an int const &. Even though int const &operator*() const is
available compilation fails. This problem can be solved in two ways: noting
that an int & can be converted to an int const & the predefined
concept std::convertible_to instead of std::same_as can be used in
ConstDereferenceable; alternatively its requires clause can specify
Type const &type instead of just Type type. Here is a definition of
ConstDereferenceable that, when defining the concept FwdIter, can be
used in combination with Dereferenceable:
template <typename Type>
concept ConstDereferenceable =
requires(Type const &type)
{
{ *type } -> std::same_as<typename Type::value_type const &>;
};
The final two iterator types pose no problems: the concept BiIterator
requires the constraints of the concept FwdIterator as well as decrement
operators, and finally the concept RndIterator requires the constraints of
BiIterator and in addition iterator increments decrements for any step
size as well as the possibility to subtract iterators:
template <typename Type>
concept BiIterator =
FwdIterator<Type> and
requires(Type type)
{
--type;
type--;
};
template <typename Type>
concept RndIterator =
BiIterator<Type>
and
requires(Type lhs, Type rhs)
{
lhs += 0;
lhs -= 0;
lhs + 0;
lhs - 0;
{ lhs - rhs } -> std::same_as<int>;
};
std::same_as. The C++20 standard provides some 30 predefined concepts which
may be used to specify type requirements, to specify conversion requirements,
and to specify more advanced requirements, sometimes accepting variadic
template parameters. The currently predefined concepts are covered in the
following subsections.
template <typename Type>
concept Name =
... requirements ...
;
When used in compound requirements only their names have to be
specified. For example (using the concept std::boolean (see below)), to
require that a function fun receiving an argument of some type Type
returns a boolean value, the following concept could be defined:
template<typename Type>
concept BoolFun =
requires(Type param)
{
{ fun(param) } -> std::boolean;
};
boolean:
copy_constructible:
copyable:
default_initializable:
destructible:noexcept(true);
equality_comparable:operator== is available to compare
two objects of its type;
floating_point:
integral:
movable:
move_constructible:
regular:semiregular and equality_comparable concepts;
semiregular:
signed_integral:
swappable:swappable_with;
unsigned_integral:
totally_ordered:==, !=, <, <=, >, and
>=. The requirements for ordering is strict:
for any two objects one and two either one < two, one == two,
or one > two is true. The generic variant is named
totally_ordered_with.
template <typename LHS, typename RHS>
concept Name =
... requirements ...
;
When used in compound requirements the compiler deduces the type of the
compound expression, and then uses that type as LHS. In the type requirement
following the compound statement only the RHS type is specified. For example
(using the concept std::same_as (see below)), to require that a function
fun, receiving an argument of some type Type, returns a
std::string the following concept can be defined:
template<typename Type>
concept StringFun =
requires(Type param)
{
{ fun(param) } -> std::same_as<std::string>;
};
assignable_from:
common_reference_with:template <typename LHS, typename RHS>
concept CommonRef = std::common_reference_with<LHS, RHS>;
template <typename T1, typename T2>
requires CommonRef<T1, T2>
void fun(T1 &&t1, T2 &&t2)
{}
struct B
{};
struct D1: public B
{
};
int main()
{
fun(4, 'a');
fun(4.5, 'a');
D1 d1;
B b;
fun(b, d1); // objects, rvalue refs:
fun(D1{}, B{}); // all OK
}
common_with:
convertible_to:template <typename LHS, typename RHS>
concept Convertible =
requires(LHS lhs)
{
{ lhs } -> std::convertible_to<RHS>;
};
template <typename RHS, typename LHS>
requires Convertible<LHS, RHS>
void fun(LHS lhs)
{}
int main()
{ // note: LHS is the <...>'s type
fun<double>(12); // from int to double
fun<int>(12.5); // from double to int
fun<std::string>("a"); // from NTBS to string
// fun<std::string>(12); // constraints not satisfied
}
derived_from:
equality_comparable_with:operator== and
operator!= are available to compare LHS- and RHS-type variables (in
any order);
same_as:std::same_as<long
int, int> does not satisfy the requirement. If such a strict equality
isn't really required then convertible_to might offer a workable
alternative;
swappable_with:swappable;
totally_ordered_with:==, !=, <, <=, >, and
>=. The requirements for ordering is strict:
for any two objects one and two either one < two, one == two,
or one > two is true. The more restrictive variant requiring objects
of identical types is named totally_ordered.
constructible_from:template <typename LHS, typename ...Args>
concept Constructible = std::constructible_from<LHS, Args...>;
template <typename T1, typename ...Args>
requires Constructible<T1, Args...>
T1 fun(Args &&...t2)
{
return T1( std::forward<Args>(t2)... );
}
int main()
{
std::string s{ fun<std::string>(5, 'a') };
std::string s2{ fun<std::string>() }; // slightly weird...
}
equivalence_relation:std::relation (see below);
invocable:invocable's first argument. Here is an example:
template <typename Function, typename ...Params>
void fun(Function &&fun, Params &&...params)
requires std::invocable<Function, Params ...>
{
fun(std::forward<Params>(params)...);
}
void hello(int value, char const *txt, std::string const &str)
{
std::cout << value << ' ' << txt << ' ' << str << '\n';
}
int main()
{
fun(hello, 1, "text", "string"); // promotions are still OK
// fun(hello, 1); // WC: not invocable
}
predicate:bool value), expecting arguments of the variadic template
parameter RHS. Here is an example:
template <typename Container, typename Predicate>
concept Find_ifConcept =
std::predicate<Predicate, typename Container::value_type>
and
requires(Container container)
{
{ container.begin() } -> Iter;
{ container.end() } -> Iter;
{ container.size() } -> std::same_as<size_t>;
};
template <typename Container, typename Predicate>
size_t findIdx_if(Container const &cont, size_t from, Predicate const &pred)
requires Find_ifConcept<Container, Predicate>
{
auto iter = std::find_if(cont.begin() + from, cont.end(), pred);
return iter == cont.end() ? cont.size() : iter - cont.begin();
}
int main()
{
std::cout << "Index at " <<
findIdx_if(std::string{ "hello world" }, 0,
[&](int ch)
{
return ch == ' ';
}
) << '\n';
int target = 4;
fun(
[&](int value)
{
return value == target;
},
4
);
}
regular_invocable:invocable;
relation:std::relation concept are
satisfied if the predicate's first template argument is std::less, the
second argument is int and the third argument is double.
In the following example struct Less is a functor comparing the
two arguments of its function call operator. Next, the function cmp
accepts such a struct type as predicate, verifying that the predicate and
the arguments that are passed to the function satisfy the requirements of
the std::relation concept. If so the functor's return value is
returned.
Finally, in main cmp is first called with int and double
arguments (which succeeds) and then with an int and a NTBS arguments:
for the second call the constraints are not satisfied as ints and
NTBSs can't be compared, and consequently compilation fails:
template <typename LHS, typename RHS>
struct Less
{
bool operator()(LHS lhs, RHS rhs) const
{
return lhs < rhs;
}
};
template <template<typename LHS, typename RHS> typename Pred,
typename LHS, typename RHS>
bool cmp(LHS lhs, RHS rhs)
requires std::relation<Pred<LHS, RHS>, LHS, RHS>
{
return Pred<LHS, RHS>{}(lhs, rhs);
}
int main()
{
std::cout << cmp <Less>(5, 4.9) << '\n';
std::cout << cmp <Less>(5, "hello world") << '\n';
}
;
strict_weak_order:pred(one, two) and pred(two,
three) are both true, then pred(one, three) is also true;
template <HasSize ...Types>
void fun(Types &&...obj)
{
sum(std::forward<Types &&>(obj)...);
}
Here we see a variadic template, but it defines all its parameters as
constrained types by simply mentioning the concept HasSize instead of just
typename. The HasSize concept is very basic: it merely requires that
type.size() exists, returning a size_t:
template <typename Types>
concept HasSize =
requires (Types type)
{
{ type.size() } -> std::same_as<size_t>;
};
Once fun has verified that all its argument types satisfy the HasSize
requirements no additional checks are necessary. The fun function
template merely forwards its arguments to sum, a variadic template, that
simply adds the return values of the size() members of its arguments:
size_t sum()
{
return 0;
}
template <typename First, typename ...Types>
size_t sum(First &&first, Types &&...types)
{
return first.size() + sum(std::forward<Types>(types)...);
}
The wrapper function fun isn't really required. The variadic template
function summing the various size() values itself can also be defined so
that its types themselves must satisfy the HasSize concept. Here is the
definition of the variadic function template sum2 requiring precisely
that:
size_t sum2()
{
return 0;
}
template <HasSize First, HasSize ...Types>
size_t sum2(First &&first, Types &&...types)
{
return first.size() + sum2(std::forward<Types>(types)...);
}
And here is a main function calling fun and sum2:
int main()
{
fun(queue<int>{}, vector<int>{}, string{});
cout << sum2(queue<int>{}, vector<int>{}, string{}) << '\n';
}
On the other hand, the predefined concept std::constructible_from is a
variadic concept, as it accepts a LHS template parameter and a RHS parameter
pack. This concept is satisfied if the LHS parameter can be constructed
from the types specified in its RHS parameter pack. After including
type_trait defining and using such a concept is not very hard:
template <typename Class, typename ...Params>
concept Constructible = std::is_constructible<Class, Params ...>::value;
template <typename Class, typename ...Params>
requires Constructible<Class, Params ...>
void fun(Class &&type, Params &&...params)
{}
The recipe for writing variadic concepts is not very complex:
When no predefined variadic type trait is available the variadic concept must
use other means to determine whether its constraints are satisfied or not. In
those cases define your own variadic type traits. For illustration let's
assume we are looking for a variadic concept that can be used to verify that
the types of all the arguments that are passed to a variadic function template
are integral types. In this case there is no predefined type trait we can use,
so we have to define it ourselves. We define the concept IntegralOnly as a
variadic concept using our self-defined type trait allIntegralTypes, and
thereupon use it when defining a function requiring that all of its arguments
are integral values:
template <typename ...Types>
concept IntegralOnly = allIntegralTypes<Types ...>::value;
template <IntegralOnly ...Types>
void fun(Types ...types)
{}
The generic type trait allIntegralTypes merely specifies that it accepts
any number of type parameters and uses specializations to handle specific
cases. One specific case is the case were no types are specified which simply
defines a true static bool const value:
template <typename ...Types>
struct allIntegralTypes;
template <>
struct allIntegralTypes<>
{
static bool const value = true;
};
The type trait's partial specialization does the hard work: it determines
whether the first type is integral and combines that (using and) with the
value made available by the struct allIntegralType receiving the
remaining types:
template <typename First, typename ...Types>
struct allIntegralTypes<First, Types ...>
{
static bool const value = std::is_integral<First>::value and
allIntegralTypes<Types ...>::value;
};
The function fun can now be called with any number of arguments. As long
as the arguments are integral types the compilation succeeds and fun can
safely do its job.
To illustrate the various ways concepts can be used when defining function
templates the concept Addable (cf. section 23.13.1) is used in the
following examples.
template <typename Type>
requires Addable<Type>
auto add(Type const &lhs, Type const &rhs)
{
return lhs + rhs;
}
template <typename Type>
auto add(Type const &lhs, Type const &rhs) requires Addable<Type>
{
return lhs + rhs;
}
These variants allow us to specify the requirements in the most flexible
way. E.g., if the parameters should also be integral values, then the
Addable requirement is not enough, by we also need the std::integral
requirement, resulting in a function definition like
template <typename Type>
requires Addable<Type> and std::integral<Type>
auto add(Type const &lhs, Type const &rhs)
{
return lhs + rhs;
}
(which can also be used with the trailing requires specification).
If the Addable concept completely covers the arguments' requirements, then
the following abbreviated definitions can be used:
typename:
template <Addable Type>
auto add(Type const &lhs, Type const &rhs)
{
return lhs + rhs;
}
auto follows the concept's name:
auto informs the compiler that Addable is not the name of a
plain type but the name of a concept:
auto add(Addable auto const &lhs, Addable auto const &rhs)
{
return lhs + rhs;
}
In the following example the concept Addable is used when defining the
class template Data. The class Data declares a
member process, implemented below the class interface. Like the class of
which it is a member its header must also specify Addable (cf. section
23.13.1):
template <Addable Type>
class Data
{
void process();
};
template <Addable Tp> // The concept must be specified,
void Data<Tp>::process() // but the formal type name
{ // doesn't have to be `Type'
...
}
Comparably, if a class template member function can only be used when a
constraint has been satisfied (but no additional constraints apply to other
class members), the class template's header can use typename and the
(additional) constraint can be tailored to members where applicable:
template <typename Type> // generic template type parameter
class Data
{
void process() requires Addable<Type>; // additional requirement
};
template <typename X>
void Data<X>::process() requires Addable<X>
...
Types of member templates themselves may also be constrained. Here too the rule applies that the template headers of member implementations must match those of their declarations:
template <typename Type>
class Data
{
template <Addable Tp> // constraint applied to
void process(Tp par); // a member template
};
template <typename Type>
template <Addable Tp>
void Data<Type>::process(Tp par)
{
...
}
struct Handler having
the following generic implementation:
template <typename Tp>
struct Handler
{
Handler()
{
std::cout << "Generic Handler\n";
}
};
In addition to possibly type-related specializations (like a struct
Handler<Tp *> ...) a specialization requiring the availability of the
addition operator on Tp can be defined by requiring the concept
Addable:
template <Addable Tp> // constrain Tp to addable types
struct Handler<Tp>
{
Handler()
{
std::cout << "Handler for types supporting operator+\n";
}
};
When used in the following program (assuming all required headers were included), the first line of the output shows Generic Handler, while the second line shows Handler for types supporting operator+:
int main()
{
Handler<std::vector<int>>{}; // generic
Handler<int>{}; // specialized
}
The compiler, compiling main's first statement, first looks for
a specialized version of Handler. Although it finds one, that
specialization requires the availability of operator+. As that operator is
not available for std::vector the compiler does not use that
specialization. Had this been the only available implementation, then the
compiler would have reported a constraints not satisfied error. However,
there's still the generic definition which can be used for
std::vector. Therefore the compiler uses the generic definition (which is
at the same time provides a nice illustration of the SFINAE (cf. section
21.15) principle).
When instantiating the second Handler object the addition operator is
available, and so in that case the compiler selects the specialized version:
where available, specializations are used; if not, then generic template
definitions are used.
Here are some simple examples illustrating how constrained function templates are declared:
template <typename Type> // advice: define concepts in
concept Addable = // separate headers.
requires(Type lh, Type rh)
{
lh + rh;
};
template <typename Type> // declares an unconstrained
void fun(); // function template
template <Addable Type> // declares a constrained overloaded
void fun(); // function template
template <typename Type> // same, requirement follows fun
void fun() requires Addable<Type>;
template <typename Type> // same, requirement precedes fun
requires Addable<Type> void fun();
When declaring class templates their requires-clauses must precede the class names. Also, when unconstrained class templates are available the constrained class templates are in fact specializations and must be declared accordingly:
template <typename Type> // unconstrained
struct Data; // declaration
template <Addable Type> // constrained declaration
struct Data<Type>; // (i.e., a specialization)
// template <typename Type> // same specialization
// requires Addable<Type> struct Data<Type>;
Multiple constraints can also be declared:
template <typename Type> // used concepts
concept C1 = true;
template <typename Type>
concept C2 = true;
template <C1 Type> // multiply constrained
requires C2<Type> void fun(); // function template
template <typename Type> // same, using 'and'
requires C1<Type> and C2<Type> void fun();
template <typename Type> // same, trailing 'requires'
void fun() requires C1<Type> and C2<Type>;
template <typename Type>
struct Multi;
template <C1 Type> // multiply constrained
requires C2<Type> struct Multi<Type>; // class template
Although specializations may define different constraints (e.g., there may
also be a concept Subtractable), a Data specialization for
subtractable types might also be defined:
template <Subtractable Type>
struct Data<Type>
{};
But this is probably not what you want: when defining Data<vector<int>>{},
where template<typename Type> Data is merely declared, the compiler
complains about an incomplete type `struct Data<std::vector<int>>' as it
cannot use the specialization for either Addable or Subtractable. So
it falls back on the generic template, but for that one no implementation is
available, and hence it's incomplete.
Defining a template requiring two types, the first being Addable and the
second template argument being unrestricted, while a specialization is defined
requiring a Subtractable type and an int, then that also
does'n work as intended. In that case, the templates might be:
template <typename t1, typename t2> requires Addable<t1>
struct Data
{};
template <Subtractable Type>
struct Data<Type, int>
{};
Here, if the first template argument isn't a subtractable type (like a
vector<int>), and the second argument is an int then the compiler
simply won't use it because the 1st argument isn't a subtractable type.
Therefore it falls back to the first (generic) template definition. However,
that one doesn't work either, because the first argument also isn't
addable, and you receive complaints about (lh + rh) being ill-formed.
Now, as you specified int as the template's second argument chances are
that you expected a complaint about (lh - rh) being ill formed, but that
doesn't happen. In other words: using concepts still requires you to
understand what's going on. Concepts help the compiler to pinpoint reasons
for compilation failures, but in the end it's you who has to understand what
you're doing in order to grasp what the compiler is trying to tell you.
Concepts provide yet another way to define free operators, bound to the types of the nested classes' template types. When using concepts the class templates and their nested classes can be defined in their most basic form, as in:
template <typename Data>
struct String
{
struct iterator
{
using value_type = Data;
std::string::iterator d_iter;
// Note the <>: operator== is a function template
// specialization as 'iterator' is a class template
friend bool operator==<>(iterator const &lhs, iterator const &rhs);
};
iterator begin()
{
return iterator{};
}
};
Once the class interface (struct String) has been specified the concept
can be formulated. It simply requires that the arguments of the free operators
are String<Data>::iterator objects:
template<typename Type>
concept StringIterator =
std::same_as<Type,
typename String<typename Type::value_type>::iterator>;
The free operator(s) can now be defined as a function template using the
abbreviated StringIterator auto type specification:
inline bool operator==(StringIterator auto const &lhs,
StringIterator auto const &rhs)
{
return lhs.d_iter == rhs.d_iter;
}
By using concepts when defining free operators of nested classes of class templates we achieve that those operators are bound to the template types of those class templates, and that the free operators perfectly match those (nested) classes. Furthermore, when designing the class templates the software engineer can concentrate on the class's essential characteristics without having to consider special type-definitions, which are required when using the sfinae approach covered in section 22.10.2.1.