vector,
stack and queue, that are implemented as class templates. With class
templates, the algorithms and the data on which the algorithms operate are
completely separated from each other. To use a particular data structure in
combination with a particular data type only the data type needs to be
specified when defining or declaring a class template object (as in
stack<int> iStack).
In this chapter constructing and using class templates is discussed. In a sense, class templates compete with object oriented programming (cf. chapter 14), that uses a mechanism resembling that of templates. Polymorphism allows the programmer to postpone the implementation of algorithms by deriving classes from base classes in which algorithms are only partially implemented. The actual definition and processing of the data upon which the algorithms operate may be postponed until derived classes are defined. Likewise, templates allow the programmer to postpone the specification of the data upon which the algorithms operate. This is most clearly seen with abstract containers, which completely specify the algorithms and at the same time leave the data type on which the algorithms operate completely unspecified.
There exists an intriguing correspondence between the kind of polymorphism we've encountered in chapter 14 and certain uses of class templates. In their book C++ Coding Standards (Addison-Wesley, 2005) Sutter and Alexandrescu refer to static polymorphism and dynamic polymorphism. Dynamic polymorphism is what we use when overriding virtual members. Using vtables the function that is actually called depends on the type of object a (base) class pointer points at. Static polymorphism is encountered in the context of templates, and is discussed and compared to dynamic polymorphism in section 22.12.
Generally, class templates are easier to use than polymorphism. It is
certainly easier to write stack<int> istack to create a stack of ints
than to derive a new class Istack: public stack and to implement all
necessary member functions defining a similar stack of ints using object
oriented programming. On the other hand, for each different type for which an
object of a class template is defined another, possibly complete class must be
reinstantiated. This is not required in the context of object oriented
programming where derived classes use, rather than copy, the functions
that are already available in their base classes (but see also section
22.11).
Previously we've already used class templates. Objects like vector<int> vi
and vector<string> vs are commonly used. The data types for which these
templates are defined and instantiated are an inherent part of such container
types. It is stressed that it is the combination of a class template type
and its template parameter(s), rather than the mere class template's type
that defines or generates a
type. So vector<int> is a type as is
vector<string>. Such types could very well be specified through
using-declarations:
using IntVector = std::vector<int>;
using StringVector = std::vector<std::string>;
IntVector vi;
StringVector vs;
So, in case we have a
template <typename T>
void fun(T const ¶m);
we can do
vector<int> vi;
fun(vi)
and the compiler deduces T == vector<int>.
On the other hand, if we have
template <typename T>
struct Fun
{
T d_data;
Fun();
};
we cannot do
Fun fun;
since Fun is not a type, and the compiler cannot deduce what the intended
type is.
Sometimes the compiler can deduce the intended types. Consider this:
vector vi{ 1, 2, 3, 4 };
In this case the compiler deduces int from the provided values. The
compiler is smart enought to select the most general type, as in this example,
where double is deduced:
vector vi{ 1, 2.5 };
The compiler is doing its utmost to deduce types when they're not
explicitly specified, and it will stay on the safe side. So the vector is a
vector<int> in the first example and a vector<double> in the second.
Although it's nice that the compiler is willing and able to deduce types in
many situations it's at the same time a potential source of confusion. In the
first example only non-negative values are used, so why not define a
vector<unsigned> or a vector<size_t>? In the second example the
compiler deduces vector<double>, but vector<float> could very well
also have been used.
To avoid confusion, as a rule of thumb, it might be a good idea to specify the types of class templates when defining class type objects. It requires hardly any effort and it completely clarifies what you want and mean. So prefer
vector<int> vi{ 1, 2, 3 };
vector<double> vd{ 1, 2.5 };
over the definitions implicitly using types.
Starting point:
template <class ...Types> // any set of types
class Deduce
{
public:
Deduce(Types ...params); // constructors
void fun(); // a member function
};
Some definitions:
// deduce: full definition:
// --------------------------------
Deduce first{1}; // 1: int -> Deduce<int> first{1}
Deduce second; // no Types -> Deduce<> second;
Deduce &&ref = Deduce<int>{ 1 };// int -> Deduce<int> &&ref
template <class Type>
Deduce third{ static_cast<Type *>(0) };
The template third is a recipe for constructing Deduce
objects from a type that's specified for third. The pointer's type simply
is a pointer to the specified type (so, specifying third<int> implies an
int *). Now that the type of third's argument is available (i.e., an
int *) the compiler deduces that third{0} is a Deduce<int *>.
This Deduce<int *> object could, e.g., be used to initialize a named
Deduce<int *> object:
auto x = third<int>; // x's full definition: Deduce<int *> x{0}
Deduce's member functions can be used by anonymous and named objects:
x.fun(); // OK: fun called by named object
third<int>.fun(); // OK: fun called by anonymous object
Here are some examples that won't compile:
extern Deduce object; // not an object definition
Deduce *pointer = 0; // any set of types could be intended
Deduce function(); // same.
When defining objects, either using function-type or curly-brace definitions template argument deduction is realized as follows:
Deduce::Deduce constructor the imaginary
function
template <class ...Types>
Deduce<Types ...> imaginary(Types ...params);
is formed.
Let's apply this process to the class Deduce. The set of imaginary
functions matching Deduce looks like this:
// already encountered: matching
template <class ...Types> // Deduce(Types ...params)
Deduce<Types ...> imaginary(Types ...params);
// the copy constructor: matching
template <class ...Types> // Deduce(Deduce<Types ...> const &)
Deduce<Types ...> imaginary(Deduce<Types ...> const &other);
// the move constructor, matching
template <class ...Types> // Deduce(Deduce<Types ...> &&)
Deduce<Types ...> imaginary(Deduce<Types ...> &&tmp);
For the construction Deduce first{1} the first imaginary function wins
the overload contest, resulting in the template argument deduction int for
class ...Types, and hence Deduce<int> first{1} is defined.
Note that when a class template is nested under a class template, the nested
class template's name depends on the outer class type. The outer class then
provides the name qualifier for the inner class template. In such cases
template argument deduction is used for the nested class, but (as it is not
used for name qualifiers) is not used for the outer class. Here is an example:
adding a nested class template to Deduce:
template <class OuterType>
class Outer
{
public:
template <class InnerType>
struct Inner
{
Inner(OuterType);
Inner(OuterType, InnerType);
template <typename ExtraType>
Inner(ExtraType, InnerType);
};
};
// defining:
Outer<int>::Inner inner{2.0, 1};
In this case, the compiler uses these imaginary functions:
template <typename InnerType>
Outer<int>::Inner<InnerType> // copy constructor
imaginary(Outer<int>::Inner<InnerType> const &);
template <typename InnerType>
Outer<int>::Inner<InnerType> // move constructor
imaginary(Outer<int>::Inner<InnerType> &&);
template <typename InnerType> // first declared constructor
Outer<int>::Inner<InnerType> imaginary(int);
template <typename InnerType> // second declared constructor
Outer<int>::Inner<InnerType> imaginary(int, InnerType);
template <typename InnerType> // third declared constructor
template <typename ExtraType>
Outer<int>::Inner<InnerType> imaginary(ExtraType, InnerType);
Template argument deduction for calling imaginary(2.0, 1) results in
double for its first argument and int for its second. Overload
resolution then favors the last imaginary function, and so ExtraType:
double and InnerType: int. Consequently,
Outer<int>::Inner inner{ 2.0, 1 };
is defined as:
Outer<int>::Inner<int> Inner{ 2.0, 1 };
template <class T>
struct Class
{
std::vector<T> d_data;
struct Iterator
{
using type = T;
bool operator!=(Iterator const &rhs);
Iterator operator++(int);
type const &operator*() const;
// ...
};
Class();
Class(T t);
Class(Iterator begin, Iterator end);
template <class Tp>
Class(Tp first, Tp second)
{}
Iterator begin();
Iterator end();
};
The implementation of the Class constructor expecting two
Class::Iterator arguments would probably be somewhat similar to the
following:
template <class T>
Class<T>::Class(Iterator begin, Iterator end)
{
while (begin != end)
d_data.push_back(*begin++);
}
where d_data is some container storing T values. A
Class object can now constructed from a pair of Class::Iterators:
Class<int> source;
...
Class<int> dest{source.begin(), source.end()};
Here, the simple template argument deduction procedure fails to deduce the
int template argument. This fails:
Class dest{source.begin(), source.end()};
When attempting to instantiate a Class object by passing it
Class::Iterators the compiler cannot directly deduce from the provided
arguments that a Class<Class::Iterator::type> is to be used: type
isn't directly available. Compare this to Class's third constructor,
where
Class intObject{12};
allows the compiler to create an imaginary function
template <class Type>
Class <Type> imaginary(Type param)
in which case Type clearly is an int, and so a Class<int>
object is constructed.
When we try to do this for Class(Iterator, Iterator) we get
template <class Iterator>
Class<???> imaginary(Iterator, Iterator);
and here Class's template argument isn't directly related to
Iterator: the compiler cannot deduce its type and consequently compilation
fails.
A similar argument applies to the fourth constructor, which receives two Tp
arguments, which are both independent from Class's template type.
In cases like these simple type template argument deduction procedure fails. Still, not everything is lost: explicit conversions, defined as explicitly specified deduction rules which are added (below) to the class's interface can be used.
An explicitly specified deduction rule connects a class template constructor signature to a class template type. It specifies the template arguments for the class template object that is constructed using the constructor whose signature is specified. The generic syntactical form of an explicitly specified deduction rule looks like this:
class template constructor signature -> resulting class type ;
Let's apply this to Class(Iterator begin, Iterator end). Its signature is
template <class Iterator>
Class(Iterator begin, Iterator end)
Requiring that Iterator defines a typename type, we can now formulate
a resulting class type:
Class<typename Iterator::type>
Now we can combine both in an explicitly specified deduction rule (which is
added as a separate line below Class's interface):
template <class Iterator>
Class(Iterator begin, Iterator end) -> Class<typename Iterator::type>;
After adding this deduction rule to Class's interface the following
constructor calls successfully compile:
Class src{12}; // already OK
Class dest1{src.begin(), src.end()};
// begin() and end() return Class<int>::Iterator
// objects. Typename Class<int>::Iterator::type
// is defined as int, so Class<int> dest1 is
// defined.
struct Double // used at the next construction
{
using type = double;
// ... members ...
};
Class dest2{Double{}, Double{}};
// Here the struct Double defines
// typename double type, so
// Class<double> dest2 is defined.
Within classes the compiler uses (as before) the class itself when merely
referring to the class name: when referring to Class in the class
Class, the compiler considers Class to be Class<T>. So the headers
of the declaration and definition of Class's copy constructor look like
this:
Class(Class const &other); // declaration
template <class T> // definition
Class<T>::Class(Class const &other)
{
// ...
}
Sometimes the default type is not what you want, in which case the required
type must explicitly be specified. Consider what happens if add a
member dup to Class:
template <typename T>
template <typename Tp>
auto Class<T>::dup(Tp first, Tp second)
{
return Class{ first, second }; // probably not what you want
} // (see the following text)
Here, because we're inside Class the compiler deduces that
Class<T> must be returned. But in the previous section we decided that,
when initializing Class from iterators, Class<typename Tp::type>
should be constructed and returned. To accomplish that, the required type is
explicitly specified:
template <typename T>
template <typename Tp>
auto Class<T>::dup(Tp first, Tp second)
{ // OK: explicitly specified Class tyoe.
return Class<typename Tp::type>{ first, second };
}
As shown in this example, simple (implicit) or explicit deduction rules do not have to be used: they can be used in many standard situations where explicitly specifying the class's template arguments appears to be superfluous. Template argument deduction was added to the language to simplify object construction when using class templates. But in the end you don't have to use these deduction rules: it's always still possible to explicitly specify template arguments.
The new class implements a circular queue. A circular queue has a fixed
number of max_size elements. New elements are inserted at its back and
only its head and tail elements can be accessed. Only the head element can be
removed from a circular queue. Once n elements have been appended the next
element is inserted again at the queue's (physical) first position. The
circular queue allows insertions until it holds max_size elements. As long
as a circular queue contains at least one element elements may be removed from
it. Trying to remove an element from an empty circular queue or to add another
element to a full circular queue results in exceptions being thrown. In
addition to other constructors a circular queue must offer a constructor
initializing its objects for max_size elements. This constructor must make
available the memory for the max_size elements but must not call those
elements default constructors (hinting at the use of the placement new
operator). A circular queue should offer value semantics as well as a move
constructor.
Please note that in the above description the actual data type that is used for the circular queue is nowhere mentioned. This is a clear indication that our class could very well be defined as a class template. Alternatively, the class could be defined for some concrete data type which is then abstracted when converting the class to a class template.
The actual construction of a class template is provided in the next section,
where the class template CirQue (circular queue) is developed.
CirQue (circular queue). This class
template has one template type parameter, Data, representing the data type
that is stored in the circular queue. The outline of the interface of this
class template looks like this:
template<typename Data>
class CirQue
{
// member declarations
};
A class template's definition starts like a function template's definition:
template, starting a template definition or
declaration.
template: a
list containing one or more comma-separated elements is called the
template parameter list. Template parameter lists may have multiple
elements, like this:
typename Type1, typename Type2, typename Type3
When a class template defines multiple template type parameters they are matched in sequence with the list of template type arguments provided when defining objects of such a class template. Example:
template <typename Type1, typename Type2, typename Type3>
class MultiTypes
{
...
};
MultiTypes<int, double, std::string> multiType;
// Type1 is int, Type2 is double, Type3 is std::string
Data for CirQue). It is a formal (type) name, like the formal types
used in function template parameter lists.
CirQue class template has been defined it can be used to
create all kinds of circular queues. As one of its constructors expects a
size_t argument defining the maximum number of elements that can be stored
in the circular queue, circular queues could be defined like this:
CirQue<int> cqi(10); // max 10 ints
CirQue<std::string> cqstr(30); // max 30 strings
As noted in the introductory section of this chapter the combination of
name of the class template and the data type for which it is instantiated
defines a data type. Also note the similarity between defining a
std::vector (of some data type) and a CirQue (of some data type).
Like std::map containers class templates may be defined with multiple
template type parameters.
Back to CirQue. A CirQue must be capable of storing max_size
Data elements. These elements are eventually stored in memory pointed at
by a pointer Data *d_data, initially pointing to raw memory. New elements
are added at the backside of the CirQue. A pointer Data *d_back is
used to point to the location where the next element is going to be
stored. Likewise, Data *d_front points to the location of the CirQue's
first element. Two size_t data members are used to monitor the filling
state of the CirQue: d_size represents the number of elements
currently stored in the CirQue, d_maxSize represents the maximum
number of elements that the CirQue can contain. Thus, the CirQue's
data members are:
size_t d_size;
size_t d_maxSize;
Data *d_data;
Data *d_front;
Data *d_back;
Class templates may also define non-type parameters. Like the function template non-type parameters they must be (integral) constants whose values must be known at object instantiation time.
Different from function template non-type parameters the values of class template non-type parameters are not deduced by the compiler using arguments passed to class template members.
Assume we extend our design of the class template CirQue so that it
defines a second (non-type) parameter size_t Size. Our intent is to use
this Size parameter in the constructor defining an array parameter of
Size elements of type Data.
The CirQue class template now becomes (only showing the relevant
constructor):
template <typename Data, size_t Size>
class CirQue
{
// ... data members
public:
CirQue(Data const (&arr)[Size]);
...
};
template <typename Data, size_t Size>
CirQue<Data, Size>::CirQue(Data const (&arr)[Size])
:
d_maxSize(Size),
d_size(0),
d_data(operator new(Size * sizeof(Data))),
d_front(d_data),
d_back(d_data),
{
std::copy(arr, arr + Size, back_inserter(*this));
}
Unfortunately, this setup doesn't satisfy our needs as the values of
template non-type parameters are not deduced by the compiler. When the
compiler is asked to compile the following main function it reports a
mismatch between the required and actual number of template parameters:
int main()
{
int arr[30];
CirQue<int> ap{ arr };
}
/*
Error reported by the compiler:
In function `int main()':
error: wrong number of template arguments (1, should be 2)
error: provided for `template<class Data, size_t Size>
class CirQue'
*/
Defining Size as a non-type parameter having a default value doesn't
work either. The compiler always uses the default unless its value is
explicitly specified. Reasoning that Size can be 0 unless we need another
value, we might be tempted to specify size_t Size = 0 in the template's
parameter type list. Doing so we create a mismatch between the default
value 0 and the actual size of the array arr as defined in the above
main function. The compiler, using the default value, reports:
In instantiation of `CirQue<int, 0>':
...
error: creating array with size zero (`0')
So, although class templates may use non-type parameters they must always be specified like type parameters when an object of that class is defined. Default values can be specified for those non-type parameters causing the compiler to use the default when the non-type parameter is left unspecified.
Default template parameter values (either type or non-type template parameters) may not be specified when defining template member functions. In general: function template definitions (and thus: class template member functions) may not be given default template (non) type arguments. If default template arguments are to be used for class template members, they have to be specified by the class interface.
Similar to non-type parameters of function templates default argument values for non-type class template parameters may only be specified as constants:
const pointer.
short can be used when an int is
called for, a long when a double is called for).
size_t parameter is specified, an int may be used as well.
const modifier, however, may be used as their values never change.
Although our attempts to define a constructor of the class CirQue
accepting an array as its argument has failed so far, we're not yet out of
options. In the next section a method is described that does allow us
to reach our goal.
In contrast, when function templates are used, the actual template parameters are deduced from the arguments used when calling the function. This opens up an alley leading to the solution of our problem. If the constructor itself is turned into a function template (having its own template header), then the compiler will be able to deduce the non-type parameter's value and there is no need anymore to specify it explicitly using a class template non-type parameter.
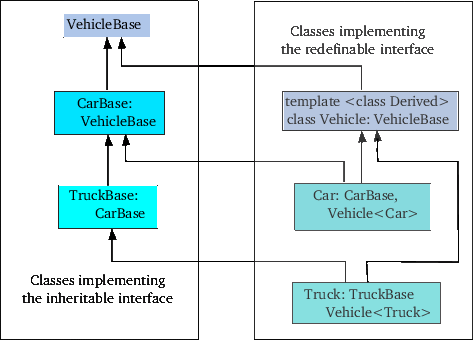
Members (functions or nested classes) of class templates that are themselves templates are called member templates.
Member templates are defined as any other template, including its own template header.
When converting our earlier CirQue(Data const (&array)[Size]) constructor
into a member template the class template's Data type parameter can still
be used, but we must provide the member template with a non-type parameter of
its own. Its declaration in the (partially shown) class interface looks like
this:
template <typename Data>
class CirQue
{
public:
template <size_t Size>
explicit CirQue(Data const (&arr)[Size]);
};
Its implementation becomes:
template <typename Data>
template <size_t Size>
CirQue<Data>::CirQue(Data const (&arr)[Size])
:
d_size(0),
d_maxSize(Size),
d_data(static_cast<Data *>(operator new(sizeof(arr)))),
d_front(d_data),
d_back(d_data)
{
std::copy(arr, arr + Size, std::back_inserter(*this));
}
The implementation uses the STL's copy algorithm and a
back_inserter adapter to insert the array's elements into the
CirQue. To use the back_inserter CirQue must provide two (public)
using-declarations (cf. section 18.2.2):
using value_type = Data;
using const_reference = const &value_type;
Member templates have the following characteristics:
template
headers must be used: the class template's template
header is specified first followed by the member template's template header;
CirQue object of a given data
type. As usual for class templates, the data type must be specified when the
object is constructed. To construct a CirQue object from the array
int array[30] we define:
CirQue<int> object(array);
CirQue,
instantiated for the formal template parameter type Data;
namespace SomeName
{
template <typename Type, ...> // class template definition
class ClassName
{
...
};
template <typename Type, ...> // non-inline member definition(s)
ClassName<Type, ...>::member(...)
{
...
}
} // namespace closes
A potentially occurring problem remains. Assume that in addition to the
above member template a CirQue<Data>::CirQue(Data const *data) has been
defined. Some (here not further elaborated) protocol could be defined allowing
the constructor to determine the number of elements that should be stored in
the CirQue object. When we now define
CirQue<int> object{ array };
it is this latter constructor, rather than the member template, that the compiler will use.
The compiler selects this latter constructor as it is a more specialized
version of a constructor of the class CirQue than the member template
(cf. section 21.14). Problems like these can be solved by
defining the constructor CirQue(Data const *data) into a member template
as well or by defining a constructor using two parameters, the second
parameter defining the number of elements to copy.
When using the former constructor (i.e., the member template) it must define a
template type parameter Data2. Here `Data' cannot be used as template
parameters of a member template may not shadow
template parameters of its
class. Using Data2 instead of Data takes care of this subtlety. The
following declaration of the constructor CirQue(Data2 const *) could
appear in CirQue's header file:
template <typename Data>
class CirQue
{
template <typename Data2>
explicit CirQue(Data2 const *data);
}
Here is how the two constructors are selected in code defining two
CirQue objects:
int main()
{
int array[30];
int *iPtr = array;
CirQue<int> ac{ array }; // calls CirQue(Data const (&arr)[Size])
CirQue<int> acPtr{ iPtr }; // calls CirQue(Data2 const *)
}
Cirque's design and construction again.
The class CirQue offers various member functions. Normal design
principles should be adhered to when constructing class template
members. Class template type parameters should preferably be defined as
Type const &, rather than Type, to prevent unnecessary copying of
large data structures. Template class constructors should use member
initializers rather than member assignment within the body of the
constructors. Member function definitions should preferably not be provided
in-class but below the class interface. Since class template member functions
are function templates their definitions should be provided in the header
file offering the class interface. They may be given the inline
attribute.
CirQue declares several constructors and (public) members (their
definitions are provided as well; all definitions are provided below the class
interface).
Here are the constructors and the destructor:
explicit CirQue(size_t maxSize = 0):CirQue capable of storing max_size Data elements. As the
constructor's parameter is given a default argument value this constructor can
also be used as a default constructor, allowing us to define, e.g., vectors of
CirQues. The constructor initializes the Cirque object's d_data
member to a block of raw memory and d_front and d_back are initialized
to d_data. As class template member functions are themselves function
templates their implementations outside of the class template's interface must
start with the class template's template header. Here is the implementation of
the CirQue(size_t) constructor:
template<typename Data>
CirQue<Data>::CirQue(size_t maxSize)
:
d_size(0),
d_maxSize(maxSize),
d_data(
maxSize == 0 ?
0
:
static_cast<Data *>(
operator new(maxSize * sizeof(Data)))
),
d_front(d_data),
d_back(d_data)
{}
CirQue(CirQue<Data> const &other):inc to increment
d_back (see below) and placement new to copy the other's Data elements
to the current object. The implementation of the copy constructor is
straightforward:
template<typename Data>
CirQue<Data>::CirQue(CirQue<Data> const &other)
:
d_size(other.d_size),
d_maxSize(other.d_maxSize),
d_data(
d_maxSize == 0 ?
0
:
static_cast<Data *>(
operator new(d_maxSize * sizeof(Data)))
),
d_front(d_data + (other.d_front - other.d_data))
{
Data const *src = other.d_front;
d_back = d_front;
for (size_t count = 0; count != d_size; ++count)
{
new(d_back) Data(*src);
d_back = inc(d_back);
if (++src == other.d_data + d_maxSize)
src = other.d_data;
}
}
CirQue(CirQue<Data> &&tmp):d_data pointer to 0 and swaps (see the
member swap, below) the temporary object with the current
object. CirQue's destructor inspects d_data and immediately
returns when it's zero. Implementation:
template<typename Data>
CirQue<Data>::CirQue(CirQue<Data> &&tmp)
:
d_data(0)
{
swap(tmp);
}
CirQue(Data const (&arr)[Size]):Size non-type parameter. It allocates
room for Size data elements and copies arr's content to the newly
allocated memory.Implementation:
template <typename Data>
template <size_t Size>
CirQue<Data>::CirQue(Data const (&arr)[Size])
:
d_size(0),
d_maxSize(Size),
d_data(static_cast<Data *>(operator new(sizeof(arr)))),
d_front(d_data),
d_back(d_data)
{
std::copy(arr, arr + Size, std::back_inserter(*this));
}
CirQue(Data const *data, size_t size):Data element and with a size_t providing the number of elements to
copy. In our current design the member template variant of this constructor is
left out of the design. As the implementation of this constructor is very
similar to that of the previous constructor, it is left as an exercise to the
reader.
~CirQue():d_data member. If it is
zero then nothing has been allocated and the destructor immediately
returns. This may occur in two situations: the circular queue contains no
elements or the information was grabbed from a temporary object by some move
operation, setting the temporary's d_data member to zero. Otherwise
d_size elements are destroyed by explicitly calling their destructors
followed by returning the element's raw memory to the common
pool. Implementation:
template<typename Data>
CirQue<Data>::~CirQue()
{
if (d_data == 0)
return;
for (; d_size--; )
{
d_front->~Data();
d_front = inc(d_front);
}
operator delete(d_data);
}
Here are Cirque's members:
CirQue &operator=(CirQue<Data> const &other): template<typename Data>
CirQue<Data> &CirQue<Data>::operator=(CirQue<Data> const &rhs)
{
CirQue<Data> tmp(rhs);
swap(tmp);
return *this;
}
CirQue &operator=(CirQue<Data> &&tmp):swap it is defined as an inline function template:
template<typename Data>
inline CirQue<Data> &CirQue<Data>::operator=(CirQue<Data> &&tmp)
{
swap(tmp);
return *this;
}
void pop_front():d_front from
the CirQue. Throws an exception if the CirQue is empty. The
exception is thrown as a CirQue<Data>::EMPTY value, defined by the
enum CirQue<Data>::Exception (see push_back). The
implementation is straightforward (explicitly calling the destructor
of the element that is removed):
template<typename Data>
void CirQue<Data>::pop_front()
{
if (d_size == 0)
throw EMPTY;
d_front->~Data();
d_front = inc(d_front);
--d_size;
}
void push_back(Data const &object):CirQue. Throws a CirQue<Data>::FULL exception if the
CirQue is full. The exceptions that can be thrown by a CirQue
are defined in its Exception enum:
enum Exception
{
EMPTY,
FULL
};
A copy of object is installed in the CirQue's raw memory using
placement new and its d_size is incremented.
template<typename Data>
void CirQue<Data>::push_back(Data const &object)
{
if (d_size == d_maxSize)
throw FULL;
new (d_back) Data(object);
d_back = inc(d_back);
++d_size;
}
void swap(CirQue<Data> &other):CirQue object
with another CirQue<Data> object;
template<typename Data>
void CirQue<Data>::swap(CirQue<Data> &other)
{
static size_t const size = sizeof(CirQue<Data>);
char tmp[size];
memcpy(tmp, &other, size);
memcpy(reinterpret_cast<char *>(&other), this, size);
memcpy(reinterpret_cast<char *>(this), tmp, size);
}
Data &back():d_back (undefined result if the CirQue is empty):
template<typename Data>
inline Data &CirQue<Data>::back()
{
return d_back == d_data ? d_data[d_maxSize - 1] : d_back[-1];
}
Data &front():d_front (undefined result if the CirQue is empty);
template<typename Data>
inline Data &CirQue<Data>::front()
{
return *d_front;
}
bool empty() const:true if the CirQue is empty;
template<typename Data>
inline bool CirQue<Data>::empty() const
{
return d_size == 0;
}
bool full() const:true if the CirQue is full;
template<typename Data>
inline bool CirQue<Data>::full() const
{
return d_size == d_maxSize;
}
size_t size() const:CirQue;
template<typename Data>
inline size_t CirQue<Data>::size() const
{
return d_size;
}
size_t maxSize() const:CirQue;
template<typename Data>
inline size_t CirQue<Data>::maxSize() const
{
return d_maxSize;
}
Finally, the class has one private member, inc, returning a
cyclically incremented pointer into CirQue's raw memory:
template<typename Data>
Data *CirQue<Data>::inc(Data *ptr)
{
++ptr;
return ptr == d_data + d_maxSize ? d_data : ptr;
}
That characteristic of templates could be refined to the point where each definition is stored in a separate function template definition file. In that case only the definitions of the function templates that are actually needed would have to be included. However, it is hardly ever done that way. Instead, the usual way to define class templates is to define the interface and to define the remaining function templates immediately below the class template's interface (defining some functions inline).
Now that the class CirQue has been defined, it can be used. To use the
class its object must be instantiated for a particular data type. In the
following example it is initialized for data type std::string:
#include "cirque.h"
#include <iostream>
#include <string>
using namespace std;
int main()
{
CirQue<string> ci(4);
ci.push_back("1");
ci.push_back("2");
cout << ci.size() << ' ' << ci.front() << ' ' << ci.back() << '\n';
ci.push_back("3");
ci.pop_front();
ci.push_back("4");
ci.pop_front();
ci.push_back("5");
cout << ci.size() << ' ' << ci.front() << ' ' << ci.back() << '\n';
CirQue<string> copy(ci);
copy.pop_front();
cout << copy.size() << ' ' << copy.front() << ' ' << copy.back() << '\n';
int arr[] = {1, 3, 5, 7, 9};
CirQue<int> ca(arr);
cout << ca.size() << ' ' << ca.front() << ' ' << ca.back() << '\n';
// int *ap = arr;
// CirQue<int> cap(ap);
}
This program produces the following output:
2 1 2
3 3 5
2 4 5
5 1 9
When defining defaults keep in mind that they should be suitable for the
majority of instantiations of the class. E.g., for the class template
CirQue the template's type parameter list could have been altered
by specifying int as its default type:
template <typename Data = int>
Even though default arguments can be specified, the compiler must still be
informed that object definitions refer to templates. When instantiating class
template objects using default template arguments the type specifications may
be omitted but the angle brackets must be retained. Assuming a default
type for the CirQue class, an object of that class may be defined
as:
CirQue<> intCirQue(10);
Default template arguments cannot be specified when defining template
members. So, the definition of, e.g., the push_back member must always
begin with the same template specification:
template <typename Data>
When a class template uses multiple template parameters, all may be given default values. Like default function arguments, once a default value is used all remaining template parameters must also use their default values. A template type specification list may not start with a comma, nor may it contain multiple consecutive commas.
template <typename Data>
class CirQue;
Default template arguments may also be specified when declaring class templates. However, default template arguments cannot be specified for both the declaration and the definition of a class template. As a rule of thumb default template arguments should be omitted from declarations, as class template declarations are never used when instantiating objects but are only occasionally used as forward references. Note that this differs from default parameter value specifications for member functions in ordinary classes. Such defaults are always specified when declaring the member functions in the class interface.
In other situations templates are instantiated when they are being used. If
this happens many times (i.e., in many different source files) then this may
slow down the compilation process considerably. Fortunately, C++ allows
programmers to prevent templates
from being instantiated, using the
extern template syntax. Example:
extern template class std::vector<int>;
Having declared the class template it can be used in its translation unit. E.g., the following function properly compiles:
#include <vector>
#include <iostream>
using namespace std;
extern template class vector<int>;
void vectorUser()
{
vector<int> vi;
cout << vi.size() << '\n';
}
But be careful:
vector header file still needs to be included to make
the features of the class vector known to the compiler. But due to the
extern template declaration none of the used members will be instantiated
for the current compilation unit;
extern template declaration. This not only holds
true for explicitly used members but hidden members (copy constructors, move
constructors, conversion operators, constructors called during promotions, to
name a few): all are assumed by the compiler to have been instantiated
elsewhere;
In a stand-alone program one might postpone defining the required members
and wait for the linker to complain about unresolved external
references. These may then be used to create a series of instantiation
declarations which are then linked to the program to satisfy the linker. Not
a very simple task, though, as the declarations must strictly match the way
the members are declared in the class interface. An easier approach is to
define an instantiation source file in which all facilities that
are used by the program are actually instantiated in a function that is never
called by the program. By adding this instantiation function to the source
file containing main we can be sure that all required members are
instantiated as well. Here is an example of how this can be done:
#include <vector>
#include <iostream>
extern void vectorUser();
int main()
{
vectorUser();
}
// this part is never called. It is added to make sure all required
// features of declared templates will also be instantiated.
namespace
{
void instantiator()
{
std::vector<int> vi;
vi.size();
}
}
std::vector<int>) looks like this:
template class std::vector<int>;
Adding this to a source file, however, will instantiate the full class, i.e., all its members are now instantiated. This may not what you want, as it might needlessly inflate your final executable.
// the compiler assumes that required members of
// vector<int> have already been instantiated elsewhere
extern template class std::vector<int>;
int main()
{
std::vector<int> vi(5); // constructor and operator[]
++vi[0]; // are NOT instantiated
}
auto to define
their parameters. When used, a lambda expression is instantiated by looking at
the actual types of arguments. Since auto is generic, different parameters
defined using auto can be instantiated to different types. Here is an
example (assuming all required headers and namespace declaration were
specified):
1: int main()
2: {
3: auto lambda = [](auto lhs, auto rhs)
4: {
5: return lhs + rhs;
6: };
7:
8: vector<int> values {1, 2, 3, 4, 5};
9: vector<string> text {"a", "b", "c", "d", "e"};
10:
11: cout <<
12: accumulate(values.begin(), values.end(), 0, lambda) << '\n' <<
13: accumulate(text.begin(), text.end(), string{}, lambda) << '\n';
14: }
The generic lambda function is defined in lines 3 through 6, and is
assigned to the lambda identifier. Then, lambda is passed to
accumulate in lines 12 and 13. In line 12 it is instantiated to add
int values, in line 13 to add std::string values: the same lambda
is instantiated to two completely different functors, which are only locally
available in main.
Generic lambda expressions are in fact class templates. To illustrate: the above example of a generic lambda expression could also have been implemented using the following class template:
struct Lambda
{
template <typename LHS, typename RHS>
auto operator()(LHS const &lhs, RHS const &rhs) const
{
return lhs + rhs;
}
};
auto lambda = Lambda{};
This identity implies that using auto in the lambda expression's
parameter list obeys the rules of template argument deduction (cf. section
21.4), which are somewhat different from the way auto normally
operates.
Another extension is the way generic lambda expressions capture outer scope variables. Previously variables could only be captured by value or by reference. As a consequence an outer scope variable of a type that only supports move construction could not be passed by value to a lambda function. This restriction was dropped, allowing variables to be initialized from arbitrary expressions. This not only allows move-initialization of variables in the lambda introducer, but with generic lambdas variables may also be initialized if they do not have a correspondingly named variable in the lambda expression's outer scope. In this case initializer expressions can be used as follows:
auto fun = [value = 1]
{
return value;
};
This lambda function (of course) returns 1: the declared capture deduces
the type from the initializer expression as if auto had been used.
To use move-initialization std::move should be used. E.g., a
unique_ptr only supports move-assignment. Here it is used to return one of
its values via a lambda function:
std::unique_ptr<int> ptr(new int(10));
auto fun = [value = std::move(ptr)]
{
return *value;
};
In generic lambda expressions the keyword auto indicates that the compiler
determines which types to use when the lambda function is instantiated. A
generic lambda expression therefore is a class template, even though it
doesn't look like one. As an example, the following lambda expression defines
a generic class template, which can be used as shown:
char const *target = "hello";
auto lambda =
[target](auto const &str)
{
return str == target;
};
vector<string> vs{stringVectorFactory()};
find_if(vs.begin(), vs.end(), lambda);
This works fine, but if you define lambda this way then you should be
prepared for complex error messages if the types of the derefenced iterators
and lambda's (silently assumed) str type don't match.
Here is a little program illustrating how generic lambda expressions can be
used in other generic lambda expressions: class templates could also have been
used. In lines 1 through 9 a generic lambda expression accumulate is
defined, defining a second paramater which is used as a function: its argument
therefore should be usable as a function. A functor definitely is, an the
second generic lambda expression lambda, defined in lines 11 through 14
provides it. In line 21 accumulate and lambda are instantiated so that
they operate on (a vector of) ints, in line 22 they are instantiated for
processing (a vector of) strings:
1: auto accumulate(auto const &container, auto function)
2: {
3: auto accu = decltype(container[0]){};
4:
5: for (auto &value: container)
6: accu = function(accu, value);
7:
8: return accu;
9: }
10:
11: auto lambda = [](auto lhs, auto rhs)
12: {
13: return lhs + rhs;
14: };
15:
16: int main()
17: {
18: vector<int> values = {1, 2, 3, 4, 5};
19: vector<string> text = {"a", "b", "c", "d", "e"};
20:
21: cout << accumulate(values, lambda) << '\n' <<
22: accumulate(text, lambda) << '\n';
23: }
In some situations generic lambdas are a bit too generic, resulting in verbose
implementations which are not required by templates in general. Consider a
generic lambda that specifies an auto &it parameter, but in addition it
should specify a parameter value of type ValueType that should be
defined by it's class. Such a parameter requires the use of a decltype
(and maybe also the use of std::decay_t) to retrieve it's actual
type. Inside the lambda's body a using declaration can be specified to
make the type available, but that again requires a verbose specification using
std::decay_t and decltype. Here is an example:
auto generic =
[](auto &it,
typename std::decay_t<decltype(it)>::ValueType value)
{
using Type = std::decay_t<decltype(it)>;
typename Type::ValueType val2{ value };
Type::staticMember();
};
To avoid this kind of verbosity generic lambda functions can also be
defined like ordinary tempates, in which case the template header immediately
follows the lambda-introducer. Using this alternative form the definition of
the generic generic lambda simply and straightforwardly becomes:
auto generic =
[]<typename Type>(Type &it, typename Type::ValueType value)
{
typename Type::ValueType val2{ value };
Type::staticMember();
};
template <typename Type>
class TheClass
{
static int s_objectCounter;
};
There will be one TheClass<Type>::objectCounter for each different
Type specification. The following object definitions result in the
instantiation of just one single static variable, shared among the two
objects:
TheClass<int> theClassOne;
TheClass<int> theClassTwo;
Mentioning static members in interfaces does not mean these members are
actually defined. They are only declared and must be defined
separately. With static members of class templates this is no different. The
definitions of static members
are usually provided immediately following (i.e., below) the template
class interface. For example, the static member
s_objectCounter's definition, positioned just below its class interface,
looks like this:
template <typename Type> // definition, following
int TheClass<Type>::s_objectCounter = 0; // the interface
Here s_objectCounter is an int and is thus independent of the
template type parameter Type. Multiple instantiations of
s_objectCounter for identical Types cause no problem, as the linker
will remove all but one instantiation from the final executable (cf. section
21.5).
In list-like constructions, where a pointer to objects of the class
itself is required, the template type parameter Type must be used when
defining the static variable. Example:
template <typename Type>
class TheClass
{
static TheClass *s_objectPtr;
};
template <typename Type>
TheClass<Type> *TheClass<Type>::s_objectPtr = 0;
As usual, the definition can be read from the variable name back to the
beginning of the definition: s_objectPtr of the class TheClass<Type>
is a pointer to an object of TheClass<Type>.
When a static variable of a template's type parameter's type is defined,
it should of course not be given the initial value 0. The default constructor
(e.g., Type()) is usually more appropriate. Example:
template <typename Type> // s_type's definition
Type TheClass<Type>::s_type = Type();
typename has been used to indicate a template type
parameter. However, it is also used to
disambiguate code inside templates. Consider the following function template:
template <typename Type>
Type function(Type t)
{
Type::Ambiguous *ptr;
return t + *ptr;
}
When this code is processed by the compiler, it complains with an -at first sight puzzling- error message like:
4: error: 'ptr' was not declared in this scope
The error message is puzzling as it was the programmer's intention to
declare a pointer to a type Ambiguous defined within the class template
Type. But the compiler, confronted with Type::Ambiguous may interpret
the statement in various ways. Clearly it cannot inspect Type itself
trying to uncover Type's true nature as Type is a template
type. Because of this Type's actual definition isn't available yet.
The compiler is confronted with two possibilities: either
Type::Ambiguous is a static member of the as yet mysterious template
Type, or it is a subtype of Type. As the standard
specifies that the compiler must assume the former, the statement
Type::Ambiguous *ptr;
is interpreted as a multiplication of the static member
Type::Ambiguous and the (now undeclared) entity ptr. The reason for
the error message should now be clear: in this context ptr is unknown.
To disambiguate code in which an identifier refers to a
subtype of a template type parameter the keyword typename must be
used. Accordingly, the above code is altered into:
template <typename Type>
Type function(Type t)
{
typename Type::Ambiguous *ptr;
return t + *ptr;
}
Classes fairly often define subtypes. When such subtypes appear inside
template definitions as subtypes of template type parameters the typename
keyword must be used to identify them as subtypes. Example: a class
template Handler defines a typename Container as its template type
parameter. It also defines a data member storing the iterator returned by the
container's begin member. In addition Handler offers a constructor
accepting any container supporting a begin member. Handler's class
interface could then look like this:
template <typename Container>
class Handler
{
Container::const_iterator d_it;
public:
Handler(Container const &container)
:
d_it(container.begin())
{}
};
What did we have in mind when designing this class?
Container represents any container supporting
iterators.
begin. The
initialization d_it(container.begin()) clearly depends on the
template's type parameter, so it's only checked for basic syntactic
correctness.
const_iterator, defined in the class Container.
typename is required. If
this is omitted and a Handler is instantiated the compiler produces a
peculiar compilation error:
#include "handler.h"
#include <vector>
using namespace std;
int main()
{
vector<int> vi;
Handler<vector<int> > ph{ vi };
}
/*
Reported error:
handler.h:4: error: syntax error before `;' token
*/
Clearly the line
Container::const_iterator d_it;
in the class Handler causes a problem. It is interpreted by the
compiler as a static member instead of a subtype. The problem is
solved using typename:
template <typename Container>
class Handler
{
typename Container::const_iterator d_it;
...
};
An interesting illustration that the compiler indeed assumes X::a to
be a member a of the class X is provided by the error message we get
when we try to compile main using the following implementation of
Handler's constructor:
Handler(Container const &container)
:
d_it(container.begin())
{
size_t x = Container::ios_end;
}
/*
Reported error:
error: `ios_end' is not a member of type `std::vector<int,
std::allocator<int> >'
*/
Now consider what happens if the function template introduced at the
beginning of this section doesn't return a Type value, but a
Type::Ambiguous value. Again, a subtype of a template type is referred to,
and typename must be used:
template <typename Type>
typename Type::Ambiguous function(Type t)
{
return t.ambiguous();
}
Using typename in the specification of a return type is further
discussed in section 23.1.1.
Typenames can be embedded in using declarations. As is often the case,
this
reduces the complexities of declarations and definitions appearing
elsewhere. In the next example the type Iterator is defined as a subtype
of the template type Container. Iterator may now be used without
requiring the use of the keyword typename:
template <typename Container>
class Handler
{
using Iterator = Container::const_iterator;
Iterator d_it;
...
};
CirQue can be used for many different types. Their common
characteristic is that they can simply be pointed at by the class's d_data
member. But this is not always as simple as it looks. What if Data turns
out to be a vector<int>? For such data types the vanilla CirQue
implementation cannot be used and a specialization could be considered. When
considering a specialization one should also consider inheritance. Often a
class derived from the class template accepting the incompatible data
structure as its argument but otherwise equal to the original class template
can easily be designed. The developmental advantage of inheritance over
specialization is clear: the inherited class inherits the members of its base
class while the specialization inherits nothing. All members defined by the
original class template must be implemented again by the class template's
specialization.
The specialization considered here is a true specialization in that the
data members and representation used by the specialization greatly differ from
the original CirQue class template. Therefore all members defined by the
orginal class template must be modified to fit the specialization's data
organization.
Like function template specializations class template specializations
start with a template header that may or may not have an empty template
parameter list. If the template parameters are directly specialized by the
specialization it remains empty (e.g., CirQue's template type parameter
Data is specialized for char * data). But the template parameter list
may show typename Data when specializing for a vector<Data>, i.e., a
vector storing any type of data. This leads to the following principle:
A template specialization is recognized by the template argument list following a function or class template's name and not by an empty template parameter list. Class template specializations may have non-empty template parameter lists. If so, a partial class template specialization is defined.
A completely specialized class has the following characteristics:
template <> header, but must immediately start with the member function's
header.
CirQue class, specialized
for a vector<int>. All members of the specialized class are declared, but
only non-trivial implementations of its members are provided. The specialized
class uses a copy of the vector passed to the constructor and implements a
circular queue using its vector data member:
#ifndef INCLUDED_CIRQUEVECTOR_H_
#define INCLUDED_CIRQUEVECTOR_H_
#include <vector>
#include "cirque.h"
template<>
class CirQue<std::vector<int>>
{
using IntVect = std::vector<int>;
IntVect d_data;
size_t d_size;
using iterator = IntVect::iterator;
iterator d_front;
iterator d_back;
public:
using value_type = int;
using const_reference = const &value_type;
enum Exception
{
EMPTY,
FULL
};
CirQue();
CirQue(IntVect const &iv);
CirQue(CirQue<IntVect> const &other);
CirQue &operator=(CirQue<IntVect> const &other);
int &back();
int &front();
bool empty() const;
bool full() const;
size_t maxSize() const;
size_t size() const;
void pop_front();
void push_back(int const &object);
void swap(CirQue<IntVect> &other);
private:
iterator inc(iterator const &iter);
};
CirQue<std::vector<int>>::CirQue()
:
d_size(0)
{}
CirQue<std::vector<int>>::CirQue(IntVect const &iv)
:
d_data(iv),
d_size(iv.size()),
d_front(d_data.begin()),
d_back(d_data.begin())
{}
CirQue<std::vector<int>>::CirQue(CirQue<IntVect> const &other)
:
d_data(other.d_data),
d_size(other.d_size),
d_front(d_data.begin() + (other.d_front - other.d_data.begin())),
d_back(d_data.begin() + (other.d_back - other.d_data.begin()))
{}
CirQue<std::vector<int>> &CirQue<std::vector<int>>::operator=(
CirQue<IntVect> const &rhs)
{
CirQue<IntVect> tmp(rhs);
swap(tmp);
}
void CirQue<std::vector<int>>::swap(CirQue<IntVect> &other)
{
char tmp[sizeof(CirQue<IntVect>)];
memcpy(tmp, &other, sizeof(CirQue<IntVect>));
memcpy(reinterpret_cast<char *>(&other), this, sizeof(CirQue<IntVect>));
memcpy(reinterpret_cast<char *>(this), tmp, sizeof(CirQue<IntVect>));
}
void CirQue<std::vector<int>>::pop_front()
{
if (d_size == 0)
throw EMPTY;
d_front = inc(d_front);
--d_size;
}
void CirQue<std::vector<int>>::push_back(int const &object)
{
if (d_size == d_data.size())
throw FULL;
*d_back = object;
d_back = inc(d_back);
++d_size;
}
inline int &CirQue<std::vector<int>>::back()
{
return d_back == d_data.begin() ? d_data.back() : d_back[-1];
}
inline int &CirQue<std::vector<int>>::front()
{
return *d_front;
}
CirQue<std::vector<int>>::iterator CirQue<std::vector<int>>::inc(
CirQue<std::vector<int>>::iterator const &iter)
{
iterator tmp(iter + 1);
tmp = tmp == d_data.end() ? d_data.begin() : tmp;
return tmp;
}
#endif
The next example shows how to use the specialized CirQue class:
static int iv[] = {1, 2, 3, 4, 5};
int main()
{
vector<int> vi(iv, iv + 5);
CirQue<vector<int>> ci(vi);
cout << ci.size() << ' ' << ci.front() << ' ' << ci.back() << '\n';
ci.pop_front();
ci.pop_front();
CirQue<vector<int>> cp;
cp = ci;
cout << cp.size() << ' ' << cp.front() << ' ' << cp.back() << '\n';
cp.push_back(6);
cout << cp.size() << ' ' << cp.front() << ' ' << cp.back() << '\n';
}
/*
Displays:
5 1 5
3 3 5
4 3 6
*/
Function templates cannot be partially specialized: there is no need for that, as a `partially specialized function template' merely is a function template that is tailored to particular types of some of its parameters. Since function templates can be overloaded, `partially specializing' a function template simply means that overloads have to be defined for those specialized parameter types.
With partial specializations a subset (any subset) of template type parameters are given specific values. It is also possible to use a class template partial specialization when the intent is to specialize the class template, but to parameterize the data type that is processed by the specialization.
To start our discussion with an example of the latter use of a partial class
template specialization consider the class CirQue<vector<int>>
developed in the previous section. When designing CirQue<vector<int>>
you may have asked yourself how many specializations you'd have to
implement. One for vector<int>, one for vector<string>, one for
vector<double>? As long as the data types handled by the vector used
by the class CirQue<vector<...>> behaves like an int (i.e., is a
value-type of class) the answer is: zero. Instead of defining full
specializations for each new data type the data type itself can be
parameterized, resulting in a partial specialization:
template <typename Data>
class CirQue<std::vector<Data>>
{
...
};
The above class is a specialization as a template argument list is
appended to the CirQue class name. But as the class template itself has a
non-empty template parameter list it is in fact recognized as a partial
specialization. There is one characteristic that distinguishes the
implementation (subsequent to the class template's interface) of a class
template member function of a partial specialization from the implementation
of a member function of a full specialization. Implementations of partially
specialized class template member functions receive a template header. No
template headers are used when implementing fully specialized class template
members.
Implementing the partial specialization for CirQue is not difficult and is
left as an exercise for the reader (hints: simply change int into Data
in the CirQue<vector<int>> specialization of the previous section).
Remember to prefix the type iterator by typename (as in using
iterator = DataVect::iterator) (as discussed in section 22.2.1).
In the next subsections we'll concentrate on specializing class template non-type template parameters. These partial specializations are now illustrated using some simple concepts defined in matrix algebra, a branch of linear algebra.
A matrix is commonly thought of as a table of some rows and columns,
filled with numbers. Immediately we recognize an opening for using templates:
the numbers might be plain double values, but they could also be complex
numbers, for which our complex container (cf. section 12.5) might
prove useful. Our class template is therefore provided with a DataType
template type parameter. It is specified when a
matrix is constructed. Some simple matrices using double values, are:
1 0 0 An identity matrix,
0 1 0 (a 3 x 3 matrix).
0 0 1
1.2 0 0 0 A rectangular matrix,
0.5 3.5 18 23 (a 2 x 4 matrix).
1 2 4 8 A matrix of one row
(a 1 x 4 matrix), also known as a
`row vector' of 4 elements.
(column vectors are analogously defined)
Various operations are defined on matrices. They may, for example be added, subtracted or multiplied. Here we will not focus on these operations. Rather, we concentrate on some simple operations: computing marginals and sums.
Marginals are the sums of row elements or the sums of column elements of a matrix. These two kinds of marginals are also known as, respectively, row marginals and column marginals.
Rows) sums in corresponding
elements of a (column) vector of Rows elements.
Columns) sums in corresponding elements of a (row) vector of
Columns elements.
-------------------------------------
row
matrix marginals
---------
1 2 3 6
4 5 6 15
---------
column 5 7 9 21 (sum)
marginals
-------------------------------------
Since matrices consist of well defined numbers of rows and columns (the
dimensions of the matrix), that normally do not change when matrices are
used, we might consider specifying their values as template non-type
parameters. The DataType = double will be used in the majority of
cases. Therefore, double can be selected as the template's default type
argument. Since it's a sensible default, the DataType template type
parameter is used last in the template type parameter list.
Our template class Matrix begins its life as:
template <size_t Rows, size_t Columns, typename DataType = double>
class Matrix
...
What do we want our class template to offer?
Rows' rows each containing `Columns' elements of type
DataType. It can be an array, rather than a pointer, since the matrix'
dimensions are known a priori. Since a vector of Columns elements (a
row of the matrix), as well as a vector of Row elements (a column
of the matrix) is often used, the class could specify using-declarations to
represent them. The class interface's initial section thus contains:
using MatrixRow = Matrix<1, Columns, DataType>;
using MatrixColumn = Matrix<Rows, 1, DataType>;
MatrixRow d_matrix[Rows];
template <size_t Rows, size_t Columns, typename DataType>
Matrix<Rows, Columns, DataType>::Matrix()
{
std::fill(d_matrix, d_matrix + Rows, MatrixRow());
}
template <size_t Rows, size_t Columns, typename DataType>
Matrix<Rows, Columns, DataType>::Matrix(std::istream &str)
{
for (size_t row = 0; row < Rows; row++)
for (size_t col = 0; col < Columns; col++)
str >> d_matrix[row][col];
}
operator[] member (and its const variant) only
handles the first index, returning a reference to a complete
MatrixRow. How elements in a MatrixRow can be retrieved is shortly
covered. To keep the example simple, no array bound check has been
implemented:
template <size_t Rows, size_t Columns, typename DataType>
Matrix<1, Columns, DataType>
&Matrix<Rows, Columns, DataType>::operator[](size_t idx)
{
return d_matrix[idx];
}
Matrix. We'll define the type MatrixColumn as the
type containing the row marginals of a matrix, and the type MatrixRow as
the type containing the column marginals of a matrix.
There is also the sum of all the elements of a matrix. This sum of all the
elements of a matrix is a number that itself can be thought of as a 1 x 1
matrix.
Marginals can be considered as special forms of matrices. To represent these
marginals we can construct partial specializations defining the class
templates MatrixRow and MatrixColumn objects; and we construct a
partial specialization handling 1 x 1 matrices. These partial
specializations are used to compute marginals and the sum of all the elements
of a matrix.
Before concentrating on these partial specializations themselves we'll use them here to implement the members computing the marginals and the sum of all elements of a matrix:
template <size_t Rows, size_t Columns, typename DataType>
Matrix<1, Columns, DataType>
Matrix<Rows, Columns, DataType>::columnMarginals() const
{
return MatrixRow(*this);
}
template <size_t Rows, size_t Columns, typename DataType>
Matrix<Rows, 1, DataType>
Matrix<Rows, Columns, DataType>::rowMarginals() const
{
return MatrixColumn(*this);
}
template <size_t Rows, size_t Columns, typename DataType>
DataType Matrix<Rows, Columns, DataType>::sum() const
{
return rowMarginals().sum();
}
Matrix, mainly (but not only) used for the
construction of column marginals. Here is how such a partial specialization is
designed:
DataType = double) since defaults were already specified by the generic
class template definition. The specialization must follow the definition
of the generic class template's definition, or the compiler complains that it
doesn't know what class is being specialized. Following the template header,
the class's interface starts. It's a class template (partial) specialization
so the class name must be followed by a template argument list specifying the
template arguments used by the partial specialization. The arguments specify
explicit types or values for some of the template's parameters. Remaining
types are simply copied from the class template partial specialization's
template parameter list. E.g., the MatrixRow specialization specifies 1
for the generic class template's Rows non-type parameter (as we're talking
here about a single row). Both Columns and DataType remain to be
specified. The MatrixRow partial specialization therefore starts as
follows:
template <size_t Columns, typename DataType> // no default allowed
class Matrix<1, Columns, DataType>
MatrixRow holds the data of a single row. So it needs a
data member storing Columns values of type DataType. Since Columns
is a constant value, the d_row data member can be defined as an array:
DataType d_column[Columns];
MatrixRow's data elements using DataType's default constructor:
template <size_t Columns, typename DataType>
Matrix<1, Columns, DataType>::Matrix()
{
std::fill(d_column, d_column + Columns, DataType());
}
Another constructor is needed initializing a MatrixRow object
with the column marginals of a generic Matrix object. This requires us to
provide the constructor with a non-specialized Matrix parameter.
The rule of thumb here is to define a member template that allows us to
keep the general nature of the parameter. The generic Matrix
template requires three template parameters. Two of these were already
provided by the template specialization. The third parameter is mentioned in
the member template's template header. Since this parameter refers to the
number of rows of the generic matrix it is simply called Rows.
Here then is the implementation of the second constructor, initializing the
MatrixRow's data with the column marginals of a generic Matrix object:
template <size_t Columns, typename DataType>
template <size_t Rows>
Matrix<1, Columns, DataType>::Matrix(
Matrix<Rows, Columns, DataType> const &matrix)
{
std::fill(d_column, d_column + Columns, DataType());
for (size_t col = 0; col < Columns; col++)
for (size_t row = 0; row < Rows; row++)
d_column[col] += matrix[row][col];
}
The constructor's parameter is a reference to a Matrix template using
the additional Row template parameter as well as the template parameters
of the partial specialization.
MatrixRow an overloaded
operator[]() is of course useful. Again, the const variant can be
implemented like the non-const variant. Here is its implementation:
template <size_t Columns, typename DataType>
DataType &Matrix<1, Columns, DataType>::operator[](size_t idx)
{
return d_column[idx];
}
Matrix class and the
partial specialization defining a single row the compiler selects the
row's specialization whenever a Matrix is defined using Row = 1. For
example:
Matrix<4, 6> matrix; // generic Matrix template is used
Matrix<1, 6> row; // partial specialization is used
MatrixColumn is constructed
similarly. Let's present its highlights (the full Matrix class template
definition as well as all its specializations are provided in the
cplusplus.yo.zip archive (that can be obtained from the C++ Annotations'
Gitlab website) in the
file yo/classtemplates/examples/matrix.h):
template <size_t Rows, typename DataType>
class Matrix<Rows, 1, DataType>
MatrixRow constructors were implemented. Their implementations are
left as an exercise to the reader (and they can be found in matrix.h).
sum is defined to compute the sum of the
elements of a MatrixColumn vector. It's simply implemented
using the accumulate generic algorithm:
template <size_t Rows, typename DataType>
DataType Matrix<Rows, 1, DataType>::sum()
{
return std::accumulate(d_row, d_row + Rows, DataType());
}
Matrix<1, 1> cell;
Is this a MatrixRow or a MatrixColumn specialization? The answer
is: neither.
It's ambiguous, precisely because both the columns and the rows could
be used with a (different) template partial specialization. If such a
Matrix is actually required, yet another specialized template must be
designed.
Since this template specialization can be useful to obtain the sum of the
elements of a Matrix, it's covered here as well.
DataType. The class definition specifies
two fixed values: 1 for the number of rows and 1 for the number of columns:
template <typename DataType>
class Matrix<1, 1, DataType>
Matrix type are again implemented as
member templates. For example:
template <typename DataType>
template <size_t Rows, size_t Columns>
Matrix<1, 1, DataType>::Matrix(
Matrix<Rows, Columns, DataType> const &matrix)
:
d_cell(matrix.rowMarginals().sum())
{}
template <typename DataType>
template <size_t Rows>
Matrix<1, 1, DataType>::Matrix(Matrix<Rows, 1, DataType> const &matrix)
:
d_cell(matrix.sum())
{}
Matrix<1, 1> is basically a wrapper around a DataType
value, we need members to access that latter value. A type conversion
operator might be useful, but we also defined a get member to obtain
the value if the conversion operator isn't used by the compiler (which
happens when the compiler is given a choice, see section
11.3). Here are the accessors (leaving out their const
variants):
template <typename DataType>
Matrix<1, 1, DataType>::operator DataType &()
{
return d_cell;
}
template <typename DataType>
DataType &Matrix<1, 1, DataType>::get()
{
return d_cell;
}
Finally, the main function shown below illustrates how the Matrix
class template and its partial specializations can be used:
#include <iostream>
#include "matrix.h"
using namespace std;
int main(int argc, char **argv)
{
Matrix<3, 2> matrix(cin);
Matrix<1, 2> colMargins(matrix);
cout << "Column marginals:\n";
cout << colMargins[0] << " " << colMargins[1] << '\n';
Matrix<3, 1> rowMargins(matrix);
cout << "Row marginals:\n";
for (size_t idx = 0; idx < 3; idx++)
cout << rowMargins[idx] << '\n';
cout << "Sum total: " << Matrix<1, 1>(matrix) << '\n';
}
/*
Generated output from input: 1 2 3 4 5 6
Column marginals:
9 12
Row marginals:
3
7
11
Sum total: 21
*/
Variadic templates are defined for function templates and for class templates. Variadic templates allow us to specify an arbitrary number of template arguments of any type.
Variadic templates were added to the language to prevent us from having to define many overloaded templates and to be able to create type safe variadic functions.
Although C (and C++) support variadic functions, their use has always been deprecated in C++ as those functions are notoriously type-unsafe. Variadic function templates can be used to process objects that until now couldn't be processed properly by C-style variadic functions.
Template headers of variadic templates use the phrase
typename ...Params (Params being a formal
name). A variadic class template Variadic could be declared as follows:
template<typename ...Params> class Variadic;
Assuming the class template's definition is available then this template can be instantiated using any number of template arguments. Example:
class Variadic<
int,
std::vector<int>,
std::map<std::string, std::vector<int>>
> v1;
The template argument list of a variadic template can also be empty. Example:
class Variadic<> empty;
If this is considered undesirable using an empty template argument list can be prevented by providing one or more fixed parameters. Example:
template<typename First, typename ...Rest>
class tuple;
C's function printf is a well-known example of a type-unsafe
function. It is turned into a type-safe function when it is implemented as a
variadic function template. Not only does this turn the function into a
type-safe function but it is also automatically extended to accept any type
that can be defined by C++. Here is a possible declaration of a variadic
function template printcpp:
template<typename ...Params>
void printcpp(std::string const &strFormat, Params ...parameters);
The ellipsis (...) used in the declaration serves two purposes:
sizeof operator:
template<typename ...Params>
struct StructName
{
enum: size_t { s_size = sizeof ...(Params) };
};
// StructName<int, char>::s_size -- initialized to 2
By defining a partial specialization of a variadic template, explicitly
defining an additional template type parameter, we can associate the first
template argument of a parameter pack with this additional (first) type
parameter. The setup of such a variadic function template (e.g., printcpp,
see the previous section) is as follows:
printcpp function receives at least a format
string. Following the format string any number of additional arguments may be
specified.
First. The types of any remaining
arguments are bound to the template function's second template parameter,
which is a parameter pack.
First parameter. As
this reduces the size of the recursive call's parameter pack the recursion
eventually stops.
The overloaded non-template function prints the remainder of the format string, en passant checking for any left-over format specifications:
void printcpp(string const &format)
{
size_t left = 0;
size_t right = 0;
while (true)
{
if ((right = format.find('%', right)) == string::npos)
break;
if (format.find("%%", right) != right)
throw std::runtime_error(
"printcpp: missing arguments");
++right;
cout << format.substr(left, right - left);
left = ++right;
}
cout << format.substr(left);
}
Here is the variadic function template's implementation:
template<typename First, typename ...Params>
void printcpp(std::string const &format, First value, Params ...params)
{
size_t left = 0;
size_t right = 0;
while (true)
{
if ((right = format.find('%', right)) == string::npos) // 1
throw std::runtime_error("printcpp: too many arguments");
if (format.find("%%", right) != right) // 2
break;
++right;
cout << format.substr(left, right - left);
left = ++right;
}
cout << format.substr(left, right - left) << value;
printcpp(format.substr(right + 1), params...);
}
%. If none is found then the function is called with too many arguments
and it throws an exception;
%%. If only a single
% has been seen the while-loop ends, the format string is inserted
into cout up to the % followed by value, and the recursive call
receives the remaing part of the format string as well as the remaining
parameter pack;
%% was seen the format string is inserted up to the second
%, which is ignored, and processing of the format string continues beyond
the %%.
printcpp when compiling the function
template.
Different from C's printf function printcpp only recognizes
% and %% as format specifiers. The above implementation does not
recognize, e.g., field widths. Type specifiers like %c and %x are of
course not needed as ostream's insertion operator is aware of the types of
the arguments that are inserted into the ostream. Extending the format
specifiers so that field widths etc. are recognized by this printcpp
implementation is left as an exercise to the reader. Here is an example
showing how printcpp can be called:
printcpp("Hello % with %%main%% called with % args"
" and a string showing %\n",
"world", argc, "A String"s);
string's member insert. String::insert has several
overloaded implementations. It can be used to insert text (completely or
partially) provided by a string or by a char const * argument; to
insert single characters a specified number of times; iterators can be used to
specify the range of characters to be inserted; etc., etc.. All in all,
string offers as many as five overloaded insert members.
Assume the existence of a class Inserter that is used to insert
information into all kinds of objects. Such a class could have a string
data member into which information can be inserted. Inserter's interface
only partially has to copy string's interface to realize this: only
string::insert's interfaces must be duplicated. The members duplicating
interfaces often contain one statement (calling the appropriate member
function of the object's data member) and are for this reason often
implemented in-line. Such wrapper functions merely forward their
parameters to the matching member functions of the object's data member.
Another example is found in factory functions that also frequently forward their parameters to the constructors of objects that they return.
C++ simplifies and generalizes forwarding of parameters by offering perfect forwarding, implemented through rvalue references and variadic templates. With perfect forwarding the arguments passed to functions are `perfectly forwarded' to nested functions. Forwarding is called perfect as the arguments are forwarded in a type-safe way. To use perfect forwarding nested functions must define parameter lists matching the forwarding parameters both in types and number.
Perfect forwarding is easily implemented:
Params &&...params);
std::forward is used to forward the forwarding function's
arguments to the nested function, keeping track of their types and
number. Before forward can be used the <utility> header file
must be included.
std::forward<Params>(params)....
In the next example perfect forwarding is used to implement one member
Inserter::insert that can be used to call any of the five overloaded
string::insert members. The insert function that's actually called now
simply depends on the types and number of arguments that are passed to
Inserter::insert:
class Inserter
{
std::string d_str; // somehow initialized
public:
// constructors not implemented,
// but see below
Inserter();
Inserter(std::string const &str);
Inserter(Inserter const &other);
Inserter(Inserter &&other);
template<typename ...Params>
void insert(Params &&...params)
{
d_str.insert(std::forward<Params>(params)...);
}
};
A factory function returning an Inserter can also easily be implemented
using perfect forwarding. Rather than defining four overloaded factory
functions a single one now suffices. By providing the factory function with an
additional template type parameter specifying the class of the object to
construct the factory function is turned into a completely general factory
function:
template <typename Class, typename ...Params>
Class factory(Params &&...params)
{
return Class(std::forward<Params>(params)...);
}
Here are some examples showing its use:
Inserter inserter(factory<Inserter>("hello"));
string delimiter(factory<string>(10, '='));
Inserter copy(factory<Inserter>(inserter));
The function std::forward is provided by the standard library. It
performs no magic, but merely returns params as a nameless object. That
way it acts like std::move that also removes the name from an object,
returning it as a nameless object. The unpack operator has nothing to do with
the use of forward but merely tells the compiler to apply forward to
each of the arguments in turn. Thus it behaves similarly to C's ellipsis
operator used by variadic functions.
Perfect forwarding was introduced in section 21.4.5: a template
function defining a Type &¶m, with Type being a template type
parameter converts Type && to Tp & if the function is called with
an argument of type Tp &. Otherwise it binds Type to Tp,
with param being defined as Tp &¶m. As a result an lvalue
argument binds to an lvalue-type (Tp &), while an rvalue argument
binds to an rvalue-type (Tp &&).
The function std::forward merely passes the argument (and its type) on to
the called function or object. Here is its simplified implementation:
typedef <type T>
T &&forward(T &&a)
{
return a;
}
Since T && turns into an lvalue reference when forward is called
with an lvalue (or lvalue reference) and remains an rvalue reference if
forward is called with an rvalue reference, and since forward (like
std::move) anonymizes the variable passed as argument to forward, the
argument value is forwarded while passing its type from the function's
parameter to the called function's argument.
This is called perfect forwarding as the nested function can only be
called if the types of the arguments that were used when calling the `outer'
function (e.g., factory) exactly match the types of the parameters of the
nested function (e.g., Class's constructor). Perfect forwarding therefore
is a tool to realize type safety.
A cosmetic improvement to forward requires users of forward to
specify the type to use rather than to have the compiler deduce the type as a
result of the function template parameter type deduction's process. This is
realized by a small support struct template:
template <typename T>
struct identity
{
using type = T;
};
This struct merely defines identity::type as T, but as it is a
struct it must be specified explicitly. It cannot be determined from the
function's argument itself. The subtle modification to the above
implementation of forward thus becomes (cf. section 22.2.1 for
an explanation of the use of typename):
typedef <type T>
T &&forward(typename identity<T>::type &&arg)
{
return arg;
}
Now forward must explicitly state arg's type, as in:
std::forward<Params>(params)
Using the std::forward function and the rvalue reference specification
is not restricted to the context of parameter packs. Because of the special
way rvalue references to template type parameters are treated (cf. section
21.4.5) they can profitably be used to forward individual function
parameters as well. Here is an example showing how an argument to a function
can be forwarded from a template to a function that is itself passed to the
template as a pointer to an (unspecified) function:
template<typename Fun, typename ArgType>
void caller(Fun fun, ArgType &&arg)
{
fun(std::forward<ArgType>(arg));
}
A function display(ostream &out) and increment(int &x) may now
both be called through caller. Example:
caller(display, cout);
int x = 0;
caller(increment, x);
The unpack operator can also be used to define template classes that are derived from any number of base classes. Here is how it's done:
template <typename ...BaseClasses>
class Combi: public BaseClasses... // derive from base classes
{
public:
// specify base class objects
// to its constructor using
// perfect forwarding
Combi(BaseClasses &&...baseClasses)
:
BaseClasses(baseClasses)... // use base class initializers
{} // for each of the base
}; // classes
This allows us to define classes that combine the features of any number
of other classes. If the class Combi is derived of classes A, B, and
C then Combi is-an A, B, and C. It should of course be given a
virtual destructor. A Combi object can be passed to functions expecting
pointers or references to any of its base class type objects. Here is an
example defining Combi as a class derived from a vector of complex
numbers, a string and a pair of ints and doubles (using uniform intializers in
a sequence matching the sequence of the types specified for the used Combi
type):
using MultiTypes = Combi<
vector<complex<double>>, string, pair<int, double> >;
MultiTypes mt = { {3.5, 4}, "mt", {1950, 1.72} };
The same construction can also be used to define template data members
supporting variadic type lists such as tuples (cf. section
22.6). Such a class could be designed along these lines:
template <typename ...Types>
struct Multi
{
std::tuple<Types...> d_tup; // define tuple for Types types
Multi(Types ...types)
: // initialize d_tup from Multi's
d_tup(std::forward<Types>(types)...) // arguments
{}
};
The ellipses that are used when forwarding parameter packs are
essential. The compiler considers their omission an error. In the following
struct definition it was the intent of the programmer to pass a parameter
pack on to a nested object construction but ellipses were omitted while
specifying the template parameters, resulting in a
parameter packs not expanded with `...' error message:
template <int size, typename ...List>
struct Call
{
Call(List &&...list)
{
Call<size - 1, List &&> call(std::forward<List>(list)...);
}
};
Instead of the above definition of the call object the programmer
should have used:
Call<size - 1, List &&...> call(std::forward<List>(list)...);
int values, forwarding these values to a class template. The class
template defines an enum value result which is returned by the
function, unless no int values were specified, in which case 0 is returned.
template <int ... Ints>
int forwarder()
{
return computer<Ints ...>::result; // forwarding the Ints
}
template <> // specialization if no ints are provided
int forwarder<>()
{
return 0;
}
// use as:
cout << forwarder<1, 2, 3>() << ' ' << forwarder<>() << '\n';
The sizeof operator can be used for variadic non-type parameters as
well: sizeof...(Ints) would return 3 when used in the first function
template for forwarder<1, 2, 3>().
Variadic non-type parameters are used to define variadic literal operators, introduced in section 23.3.
Sometimes the arguments must be combined using binary operators (like arg1
+ arg2 + ...). In those cases a folding expression can be used instead
of combining the arguments using a traditional variadic template.
All binary operators (including the assignment, compound assignment and comma operators) can be used in folding expressions.
(... op expr)
where op is the binary operator that is used in the fold expression, and expr is an expression formulated in terms of the function parameter representing the variadic arguments. Here is an example:
template <typename ReturnType, typename ...Params>
ReturnType sum(Params ...params)
{
return (... + params);
}
If a more elaborate expression than just the designator of the variadic arguments is used then the expression must be clearly demarcated, e.g., by surrounding in with parentheses:
return (... + (2 * params));
In a unary fold expression all the function's arguments matching the types of the parameter pack are combined using specified operator. E.g.,
sum<int>(1, 2, 3);
returns 6.
ostream), or when initializing a variable or object. Also,
the types of the arguments do not have to be identical: the only requirement
is that the fully expanded expression (in the example: 1 + 2 + 3 is a
valid expression).
params identifier:
(expr op ...)
Together, unary left folds and unary right folds are called unary folds.
(expr1 op ... op expr2)
Here, either expr1 is the identifier representing the variable
arguments or expr2 must be that identifier. The other one can be any other
valid expression (as with unary folds, both expressions must be clearly
demarcated). In addition, both operators must be identical.
If a binary operator has been overloaded, it will be used where applicable. A
well-known example is of course operator<< as defined for std::ostream
objects. A binary fold defined for operator<< will not only do shifts, but
can also be used to insert a series of arguments into cout:
template <class ...Pack>
ostream &out2(ostream &out, Pack &&...args)
{
return (out << ... << args);
};
Here is another interesting example: a fold expression for the comma operator:
template <class ...Pack>
void call(Pack &&...args)
{
... , args();
};
This unary fold calls each of its arguments in sequence. Arguments could
be function addresses, function object or lambda functions. Note the use of
the rvalue reference when defining the variadic parameter list which prevents
copying of function objects that might be passed to call. Assuming that
struct Functor defines a functor, and that void function() has been
defined, then call could be called this way:
Functor functor;
call(functor, function, functor,
[]()
{
// ...
}
);
Finally: don't forget the parentheses surrounding fold expressions: they are required!
<tuple> must be
included.
Whereas std::pair containers have limited functionality and only support
two members, tuples have slightly more functionality and may contain an
unlimited number of different data types. In that respect a tuple can be
considered the `template's answer to C's struct'.
A tuple's generic declaration (and definition) uses the variadic template notation:
template <class ...Types>
class tuple;
Here is an example of its use:
using tuple_idsc = std::tuple<int, double &, std::string, char const *>;
double pi = 3.14;
tuple_idsc idsc(59, pi, "hello", "fixed");
// access a field:
std::get<2>(idsc) = "hello world";
The std::get<idx>(tupleObject) function template returns a
reference to the idxth (zero based) field of the tuple
tupleObject. The index is specified as the function template's non-type
template argument.
Type-based tuple addressing () can be used for tuple types used once in a tuple definition (if the same type is used repeatedly referring to that type introduces an ambiguity). The next example shows how to refer to the elements in the above example by type:
get<int>(idsc) // 59
get<double &>(idsc) // 3.14
get<string>(idsc) // "hello"s
get<char const *>(idsc) // "fixed"
Tuples may be constructed without specifying initial values. Primitive types are initialized to zeroes; class type fields are initialized by their default constructors. Be aware that in some situations the construction of a tuple may succeed but its use may fail. Consider:
tuple<int &> empty;
cout << get<0>(empty);
Here the tuple empty cannot be used as its int & field is an
undefined reference. However, empty's construction succeeds.
Tuples may be assigned to each other if their type lists are identical; if supported by their constituent types copy constructors are available as well. Copy construction and assignment is also available if a right-hand type can be converted to its matching left-hand type or if the left-hand type can be constructed from the matching right-hand type. Tuples (matching in number and (convertible) types) can be compared using relational operators as long as their constituent types support comparisons. In this respect tuples are like pairs.
Tuples offer the following static elements (using compile-time initialization):
std::tuple_size<Tuple>::value returns the number of
types defined for the tuple type Tuple. Example:
cout << tuple_size<tuple_idsc>::value << '\n'; // displays: 4
std::tuple_element<idx, Tuple>::type
returns the type of element idx of Tuple. Example:
tuple_element<2, tuple_idsc>::type text; // defines std::string text
The unpack operator can also be used to forward the arguments of a
constructor to a tuple data member. Consider a class Wrapper that is
defined as a variadic template:
template <typename ...Params>
class Wrapper
{
...
public:
Wrapper(Params &&...params);
};
This class may be given a tuple data member which should be initialized by
the types and values that are used when initializing an object of the class
Wrapper using perfect
forwarding. Comparable to the way a class may inherit from its template types
(cf. section 22.5.3) it may forward its types and constructor arguments
to its tuple data member:
template <typename ...Params>
class Wrapper
{
std::tuple<Params...> d_tuple; // same types as used for
// Wrapper itself
public:
Wrapper(Params &&...params)
: // initialize d_tuple with
// Wrapper's arguments
d_tuple(std::forward<Params>(params)...)
{}
};
Structured bindings, however, can also be used in a much more generic way, by associating them with tuples. By doing so structured bindings don't have to be associated with data members, but they may hold values returned by class members.
The association between structured binding declarations and tuples is very strong. In fact it is so strong that the standard explicitly allows users to define tuple specializations, even though tuple specializations live in the standard namespace, which otherwise is off-limits to programmers (except, of course, when using its features).
In order to allow structured bindings to be associated with class members the following steps must be performed:
get member templates,
using int (or another integral type) specializations, where each
specialization returns a class element (e.g., a member function).
The availability of if constexpr clauses makes it easy to combine
all these specializations into a single member template.
Alternatively, a function template defined outside of the class can be
defined, which allows associating structured bindings with class
members even if you're not the class's author. In this case the
function defines a ClassType [cv] &object parameter.
std::tuple_size<Type> is provided, defining
static size_t const value as the number of index values that can
be specified with the get<idx> function. Although defining
entities in the standard namespace is normally
off limits to ordinary programs, in
this special case such specializations are allowed by the C++
standard.
std::tuple_element<idx, Type> is provided,
defining type as the type matching the return type of
get<idx>.
The flexibility that is achieved by being able to use structured bindings this way is enormous. As long as a class offers members returning values those members can be associated with structured binding variables. The member functions don't even have to return values that are immediately available (e.g, as data members accessors) but their return values could also be computed on the spot, by simply referring to the corresponding structured binding variable.
To illustrate the abovementioned steps for associating structured bindings with class members we use these classes:
class Euclid
{
size_t d_x;
size_t d_y;
public:
Euclid(size_t x = 0, size_t y = 0);
double distance() const; // sqrt(d_x * d_x + d_y * d_y)
};
class Data
{
std::string d_text{ "hello from Data" };
Euclid d_euclid;
public:
void setXY(size_t x, size_t y);
Euclid factory() const;
double distance() const;
std::string const &text() const;
};
The first step towards allowing structured bindings for Data consists of
defining a (member) termplate get. If Data is our own class we can
add a member template get. Alternatively, if we're only interested in
accessing Data's public members we could derive a class DataGet from
Data, and provide that class with the get member template. Yet another
possibility is to define a free get function template. The get
function must return whatever we're interested in. To make the appropriate
selection we use an integral type (int, size_t, ...) selector value, and
the function template thus only has a non-type template parameter. Rather than
defining several specializations using the if constexpr clause is advised,
as it greatly simplifies the function's definition.
Our get function defines selector 0 for factory, selector 1 for
distance and selector 2 for text. The distance member simply
returns d_euclid.distance(), and Euclid::distance is run-time
evaluated using its d_x and d_y values. Thus, distance is an
example of a function that will be run-time evaluated when we're referring,
later on, to the third structured bindings variable.
Here's the definition of the member template get:
template <size_t Nr>
auto get() const
{
if constexpr (Nr == 0)
return factory();
if constexpr (Nr == 1)
return distance();
if constexpr (Nr == 2)
return text();
static_assert(Nr >= 0 and Nr < 3);
}
This function is still suboptimal. Consider its specialization for value 2: it
returns Data::text(). As auto merely inspects the returned data type,
get<2>() returns a std::string, rather than (text's) return type,
which is a std::string const &. To use the return types that are actually
returned by Data's member functions, get's return type should be
defined as decltype(auto) rather than just auto:
template <size_t Nr>
decltype(auto) get() const
...
When defining get as a free function template it must be provided with a
parameter Data const &data (or Data &data if members are used that may
modify data's data members), returning the parameter's member
functions. E.g.,
// get as a free function template:
template <size_t Nr>
decltype(auto) get(Data const &data)
{
if constexpr (Nr == 0)
return data.factory();
if constexpr (Nr == 1)
return data.distance();
... // (etc)
}
Now that step 1 has been completed, we turn our attention to the
std::tuple specializations. These specializations
are defined inside the std namespace
(using namespace std { ... } or std::tuple...).
The specialization of std::tuple_size for Data defines
static size_t const value as the number of index values
that can be specified with the get<idx> function:
template<>
struct std::tuple_size<Data>
{
static size_t const value = 3;
};
The specialization of std::tuple_element for Data returns the types
matching the various return types of the get member template. Its
implementation also provides a nice example where declval is used: the
return type of the get<Nr> specialization must be determined. But to
obtain that return type a Data object is required, which isn't available
by just mentioning Data in tupe_element's specialization. However,
declval<Data>() defines an rvalue reference, which can be passed to
get<Nr>. But the function's return value isn't required, so the object
doesn't have to be constructed. Only its return type is needed. Hence, by
surrounding the get<Nr> call by decltype no object is constructed, and
merely its return type is used:
template<size_t Nr>
struct std::tuple_element<Nr, Data>
{
using type = decltype( declval<Data>().get<Nr>() );
// if get<Nr> is a free function use:
// decltype( get<Nr>( declval<Data>() ) );
};
As tuple_size and tuple_element are directly associated with the class
Data their definitions should be provided in Data's header file, below
Data's class interface.
Here's how this could be used in a main function, showing single object
access and access using a range-based for-loop:
int main()
{
Data data;
auto &[ ef, dist, txt ] = data;
// or maybe:
// auto &&[ ef, dist, txt ] = Data{};
cout << dist << ' ' << txt << '\n';
Data array[5];
for (auto &[ ef, dist, txt]: array)
cout << "for: " << dist << ' ' << txt << '\n';
}
operator()) of such classes define parameters
then the types of those parameters may also be abstracted by defining the
function call operators themselves as member templates. Example:
template <typename Class>
class Filter
{
Class obj;
public:
template <typename Param>
Param operator()(Param const ¶m) const
{
return obj(param);
}
};
The template class Filter is a wrapper around Class, filtering
Class's function call operator through its own function call operator. In
the above example the return value of Class's function call operator is
simply passed on, but any other manipulation is of course also possible.
A type that is specified as Filter's template type argument may of
course have multiple function call operators:
struct Math
{
int operator()(int x);
double operator()(double x);
};
Math objects can now be filtered using Filter<Math> fm using
Math's first or second function call operator, depending on the actual
argument type. With fm(5) the int-version is used, with fm(12.5)
the double-version is used.
However, this scheme doesn't work if the function call operators have
different return and argument types. Because of this the following class
Convert cannot be used with Filter:
struct Convert
{
double operator()(int x); // int-to-double
std::string operator()(double x); // double-to-string
};
This problem can be tackled successfully by the class template
std::result_of<Functor(Typelist)>. Before using std::result_of the
header file <functional> must be included.
The result_of class template offers a using declaration (type),
representing the type that is returned by Functor<TypeList>. It can be
used as follows to improve the implementation of Filter:
template <typename Class>
class Filter
{
Class obj;
public:
template <typename Arg>
typename std::result_of<Class(Arg)>::type
operator()(Arg const &arg) const
{
return obj(arg);
}
};
Using this definition, Filter<Convert> fc can be constructed. Now
fc(5) returns a double, while fc(4.5) returns a
std::string.
The class Convert must define the relationships between its function call
operators and their return types. Predefined function objects (like those in
the standard template library) already do so, but self-defined function
objects must do this explicitly.
If a function object class defines only one function call operator it can
specify its return type through a using-declaration. If the above class
Convert would only define the first of its two function call operators
then the using declaration (in the class's public section) should be:
using type = double;
If multiple function call operators are defined, each with its own signature
and return type, then the association between signature and return type is set
up as follows (all in the class's public section):
struct result like this:
template <typename Signature> struct result;
struct result. Convert's first function call operator gives rise to:
template <typename Class>
struct result<Class(int)>
{
using type = double;
};
and Convert's second function call operator to:
template <typename Class>
struct result<Class(double)>
{
using type = std::string;
};
int and a double, returning a size_t
gets:
template <typename Class>
struct result<Class(int, double)>
{
using type = size_t;
};
Template parameters are also specified when default template parameter
values are specified albeit that in that case the compiler provides the
defaults (cf. section 22.4 where double is used as the default
type to use for the template's DataType parameter). The actual values or
types of template parameters are
never deduced from arguments as is done with function template
parameters. So to define a Matrix of complex-valued elements, the
following syntax is used:
Matrix<3, 5, std::complex> complexMatrix;
Since the class template Matrix uses a default data type
a matrix of double-valued elements can be defined like this:
Matrix<3, 5> doubleMatrix;
A class template object may be declared using the keyword extern.
For example, to declare the matrix complexMatrix use:
extern Matrix<3, 5, std::complex> complexMatrix;
A class template declaration suffices to compile return values or
parameters that are of class template types. Example: the following source
file may be compiled, although the compiler hasn't seen the definition of the
Matrix class template. Generic classes and (partial) specializations may
all be declared. A function expecting or returning a class template object,
reference, or parameter automatically becomes a function template itself. This
is necessary to allow the compiler to tailor the function to the types of
various actual arguments that may be passed to the function:
#include <cstddef>
template <size_t Rows, size_t Columns, typename DataType = double>
class Matrix;
template <size_t Columns, typename DataType>
class Matrix<1, Columns, DataType>;
Matrix<1, 12> *function(Matrix<2, 18, size_t> &mat);
When class templates are used the compiler must first have seen their
implementations. So, template member functions must be known to the compiler
when the template is instantiated. This does not mean that all members of
a template class are instantiated or must have been seen when a class template
object is defined.
The compiler only instantiates those members that are actually used. This
is illustrated by the following simple class Demo that has two
constructors and two members. When we use one constructor and call one member
in main note the sizes of the resulting object file and executable
program. Next the class definition is modified in that the unused constructor
and member are commented out. Again we compile and link the program. Now
observe that these latter sizes are identical to the former sizes. There are
other ways to illustrate that only used members are instantiated. The nm
program could be used. It shows the symbolic content of object files. Using
nm we'll reach the same conclusion: only template member functions that
are actually used are instantiated. Here is the class template Demo that
was used for our little experiment. In main only the first constructor
and the first member function are called and thus only these members were
instantiated:
#include <iostream>
template <typename Type>
class Demo
{
Type d_data;
public:
Demo();
Demo(Type const &value);
void member1();
void member2(Type const &value);
};
template <typename Type>
Demo<Type>::Demo()
:
d_data(Type())
{}
template <typename Type>
void Demo<Type>::member1()
{
d_data += d_data;
}
// the following members should be commented out before
// compiling for the 2nd time:
template <typename Type>
Demo<Type>::Demo(Type const &value)
:
d_data(value)
{}
template <typename Type>
void Demo<Type>::member2(Type const &value)
{
d_data += value;
}
int main()
{
Demo<int> demo;
demo.member1();
}
Code not depending on template parameters is verified by the compiler when
the template is defined. If a member function in a class template uses a
qsort function, then qsort does not depend on a template
parameter. Consequently, qsort must be known to the compiler when it
encounters qsort's function call. In practice this implies that the
<cstdlib> header file must have been read by the compiler before it
is able to compile the class template definition.
On the other hand, if a template defines a <typename Ret> template
type parameter to parameterize the return type of some template member
function as in:
Ret member();
then the compiler may encounter member or the class to which
member belongs in the following locations:
member. It won't accept a definition or declaration like Ret &&
*member, because C++ does not support functions returning pointers to
rvalue references. Furthermore, it checks whether the actual type name
that is used for instantiating the object is valid. This type name must be
known to the compiler at the object's point of instantiation.
Ret parameter must have been specified (or deduced) and at this point
member's
statements that depend on the Ret template parameter are checked for
syntactic correctness. For example, if member contains a statement
like
Ret tmp(Ret(), 15);
then this is in principle a syntactically valid statement. However, when
Ret = int the statement fails to compile as int does not have a
constructor expecting two int arguments. Note that this is not a
problem when the compiler instantiates an object of member's class. At
the point of instantiation of the object its member function `member' is
not instantiated and so the invalid int construction remains undetected.
Like ordinary classes, class templates may declare other functions and
classes as their friends. Conversely, ordinary classes may declare template
classes as their friends. Here too, the friend is constructed as a special
function or class augmenting or supporting the functionality of the declaring
class. Although the friend keyword can be used by any type of class
(ordinary or template) when using class templates the following cases
should be distinguished:
ostream objects.
If the actual values of the friend's template parameters must be equal
to the template parameters of the class declaring the friend, the friend is
said to be a bound friend class or function template. In
this case the template parameters of the template specifying the friend
declaration determine (bind) the values of the template parameters of the
friend class or function. Bound friends result in a one-to-one correspondence
between the template's parameters and the friend's template parameters.
In this case an unbound friend class or function template is declared. The template parameters of the friend class or function template remain to be specified and are not related in some predefined way to the template parameters of the class declaring the friend. If a class template has data members of various types, specified by its template parameters and another class should be allowed direct access to these data members we want to specify any of the current template arguments when specifying such a friend. Rather than specifying multiple bound friends, a single generic (unbound) friend may be declared, specifying the friend's actual template parameters only when this is required.
Concrete classes and ordinary functions can be declared as friends, but before a single member function of a class can be declared as a friend, the compiler must have seen the class interface declaring that member. Let's consider the various possibilities:
void function(std::vector<Type> &vector)
unless function itself is a template, it is not immediately clear how
and why such a friend should be constructed. One reason could be to allow the
function access to the class's private static members. In addition such
friends could instantiate objects of classes that declare them as their
friends. This would allow the friend functions direct access to such object's
private members. For example:
template <typename Type>
class Storage
{
friend void basic();
static size_t s_time;
std::vector<Type> d_data;
public:
Storage();
};
template <typename Type>
size_t Storage<Type>::s_time = 0;
template <typename Type>
Storage<Type>::Storage()
{}
void basic()
{
Storage<int>::s_time = time(0);
Storage<double> storage;
std::sort(storage.d_data.begin(), storage.d_data.end());
}
template <typename Type>
class Composer
{
friend class Friend;
std::vector<Type> d_data;
public:
Composer();
};
class Friend
{
Composer<int> d_ints;
public:
Friend(std::istream &input);
};
inline::Friend::Friend(std::istream &input)
{
std::copy(std::istream_iterator<int>(input),
std::istream_iterator<int>(),
back_inserter(d_ints.d_data));
}
sorter is declared as a friend of the class
Composer:
template <typename Type>
class Composer;
class Friend
{
Composer<int> *d_ints;
public:
Friend(std::istream &input);
void sorter();
};
template <typename Type>
class Composer
{
friend void Friend::sorter();
std::vector<Type> d_data;
public:
Composer(std::istream &input)
{
std::copy(std::istream_iterator<int>(input),
std::istream_iterator<int>(),
back_inserter(d_data));
}
};
inline Friend::Friend(std::istream &input)
:
d_ints(new Composer<int>{ input })
{}
inline void Friend::sorter()
{
std::sort(d_ints->d_data.begin(), d_ints->d_data.end());
}
In this example Friend::d_ints is a pointer member. It
cannot be a Composer<int> object as the Composer class interface
hasn't yet been seen by the compiler when it reads Friend's class
interface. Disregarding this and defining a data member Composer<int>
d_ints results in the compiler generating the error
error: field `d_ints' has incomplete type
`Incomplete type', as the compiler at this points knows of the existence
of the class Composer, but as it hasn't seen Composer's interface it
doesn't know what size the d_ints data member has.
!key1.find(key2) is probably more useful. For
the current example, operator== is acceptable:
template <typename Key, typename Value>
class Dictionary
{
friend Dictionary<Key, Value>
subset<Key, Value>(Key const &key,
Dictionary<Key, Value> const &dict);
std::map<Key, Value> d_dict;
public:
Dictionary();
};
template <typename Key, typename Value>
Dictionary<Key, Value>
subset(Key const &key, Dictionary<Key, Value> const &dict)
{
Dictionary<Key, Value> ret;
std::remove_copy_if(dict.d_dict.begin(), dict.d_dict.end(),
std::inserter(ret.d_dict, ret.d_dict.begin()),
std::bind2nd(std::equal_to<Key>(), key));
return ret;
}
Iterator is
declared as a friend of a class Dictionary. Thus, the Iterator is able
to access Dictionary's private data. There are some interesting points to
note here:
template <typename Key, typename Value>
class Iterator;
template <typename Key, typename Value>
class Dictionary
{
friend class Iterator<Key, Value>;
template <typename Key, typename Value>
template <typename Key2, typename Value2>
Iterator<Key2, Value2> Dictionary<Key, Value>::begin()
{
return Iterator<Key, Value>(*this);
}
template <typename Key, typename Value>
template <typename Key2, typename Value2>
Iterator<Key2, Value2> Dictionary<Key, Value>::subset(Key const &key)
{
return Iterator<Key, Value>(*this).subset(key);
}
Dictionary it can safely
define a std::map data member that is initialized by the friend class's
constructor. The constructor may then access the Dictionary's private data
member d_dict:
template <typename Key, typename Value>
class Iterator
{
std::map<Key, Value> &d_dict;
public:
Iterator(Dictionary<Key, Value> &dict)
:
d_dict(dict.d_dict)
{}
Iterator member begin may return a map
iterator. Since the compiler does not know what the instantiation of the map
looks like, a map<Key, Value>::iterator is a template subtype. So it
cannot be used as-is, but it must be prefixed by
typename (see the function begin's return type in the next example):
template <typename Key, typename Value>
typename std::map<Key, Value>::iterator Iterator<Key, Value>::begin()
{
return d_dict.begin();
}
Dictionary
should be able to construct an Iterator (maybe because we conceptually
consider Iterator to be a sub-type of Dictionary). This is easily
accomplished by defining Iterator's constructor in its private section,
and by declaring Dictionary to be a friend of Iterator. Consequently,
only a Dictionary can create an Iterator. By declaring the constructor
of a specific Dictionary type as a friend of Iterator's we declare
a bound friend. This ensures that only that particular type of
Dictionary can create Iterators using template parameters identical to
its own. Here is how it's done:
template <typename Key, typename Value>
class Iterator
{
friend Dictionary<Key, Value>::Dictionary();
std::map<Key, Value> &d_dict;
Iterator(Dictionary<Key, Value> &dict);
public:
In this example, Dictionary's constructor is Iterator's
friend. The friend is a template member. Other members can be declared as
a class's friend as well. In those cases their prototypes must be used, also
specifying the types of their return values. Assuming that
std::vector<Value> sortValues()
is a member of Dictionary then the matching bound friend declaration
is:
friend std::vector<Value> Dictionary<Key, Value>::sortValues();
operator==
must be available. If this is required for a template ClassTemplate,
requiring a typename Type template type argument, then
a free member
template<typename Type>
bool operator==(ClassTemplate<Type> const &lhs,
ClassTemplate<Type> const &rhs);
must have been declared prior to ClassTemplate's interface
itself. Within the class interface operator== may then be declared as a
friend, specifying operator== as a specialized function template (note the
<> following the function name) like this:
template <typename Type>
class ClassTemplate
{
friend bool operator==<>(ClassTemplate<Type> const &lhs,
ClassTemplate<Type> const &rhs);
...
};
Now that the class has been declared, operator=='s implementation may
follow.
Finally, the following example can be used as a prototype for situations where bound friends are useful:
template <typename T> // a function template
void fun(T *t)
{
t->not_public();
};
template<typename X> // a free member function template
bool operator==(A<X> const &lhs, A<X> const &rhs);
template <typename X> // a class template
class A
{ // fun() is used as friend bound to A,
// instantiated for X, whatever X may be
friend void fun<A<X>>(A<X> *);
// operator== is a friend for A<X> only
friend bool operator==<>(A<X> const &lhs, A<X> const &rhs);
int d_data = 10;
public:
A();
private:
void not_public();
};
template <typename X>
A<X>::A()
{
fun(this);
}
template <typename X>
void A<X>::not_public()
{}
template<typename X> // may access lhs/rhs's private data
bool operator==(A<X> const &lhs, A<X> const &rhs)
{
return lhs.d_data == rhs.d_data;
}
int main()
{
A<int> a;
fun(&a); // fun instantiated for A<int>.
}
operator==(iterator const &lhs, iterator const &rhs) operator is
preferred over a member operator==(iterator const &rhs) const, as the
member does not allow promotions of the lhs operand.
It is possible to define the free operator== as friend in the nested
class, which then automatically becomes a bound friend. E.g.,
#include <string>
template <typename Type>
struct String
{
struct iterator
{
std::string::iterator d_iter;
friend bool operator==(iterator const &lhs, iterator const &rhs)
{
return lhs.d_iter == rhs.d_iter;
}
};
iterator begin()
{
return iterator{};
}
};
int main()
{
String<int> str;
return str.begin() == str.begin();
}
However, this requires an in-class implementation, which should be avoided
as it combines interfaces and implementations which reduces clarity.
But when moving the implementation out of the interface we run into the
problem that operator== is a function template, which must be declared as
such in the class interface. The compiler suggests to make sure the
function template has already been declared and add '<>' after the function
name. But declaring
template <typename Type>
bool operator==(Type const &lhs, Type const &rhs);
before the struct String class template, and then implementing
operator== as
template <typename Type>
inline bool operator==(String<Type>::iterator const &lhs,
String<Type>::iterator const &rhs)
{
return lhs.d_iter == rhs.d_iter;
}
the compiler still complains, reporting declaration of 'operator==' as
non-function.
So how to solve this issue? There are two known ways to solve this problem. One was suggested by Radu Cosma (teaching assistant of our C++ course in the 2021-2022 academic year), the other solution is provided in section 23.13.7.2.
Radu proposed using an application of SFINAE: by defining a free operator
provided with a type uniquely defined by the nested class, which is then
provided with a default value in the free function's implementation, the
compiler automatically selects the appropriate overloaded function. This works
for multiple classes declaring nested classes and for classes defining
multiple nested classes alike. Here is an example of two classes each
declaring a nested class iterator:
template <typename Type>
struct String
{
struct iterator
{
using StringType_iterator = int;
friend bool operator==<>(iterator const &lhs, iterator const &rhs);
std::string::iterator d_iter;
};
iterator begin()
{
return iterator{};
}
};
template <typename Type>
struct Container
{
struct iterator
{
using ContainerType_iterator = int;
friend bool operator==<>(iterator const &lhs, iterator const &rhs);
int *d_ptr;
};
iterator begin()
{
return iterator{};
}
};
Note that the nested classes declare the free functions as function
template specializations.
Then, for each nested class an implementation of the free operator is
provided. These implementations are function templates
provided with a template type Type and a second type which is the uniquely
named int type of the nested class for which the free operator is
implemented:
template <typename Type, Type::StringType_iterator = 0>
inline bool operator==(Type const &lhs, Type const &rhs)
{
return lhs.d_iter == rhs.d_iter;
}
template <typename Type, Type::ContainerType_iterator = 0>
inline bool operator==(Type const &lhs, Type const &rhs)
{
return lhs.d_ptr == rhs.d_ptr;
}
The main function illustrates the use of both free operators:
int main()
{
String<int> str;
Container<int> cnt;
return str.begin() == str.begin() and cnt.begin() == cnt.begin();
}
Here are the syntactic conventions declaring unbound friends:
template <typename Iterator, typename Class, typename Data>
Class &ForEach(Iterator begin, Iterator end, Class &object,
void (Class::*member)(Data &));
This function template can be declared as an unbound friend in the
following class template Vector2:
template <typename Type>
class Vector2: public std::vector<std::vector<Type> >
{
template <typename Iterator, typename Class, typename Data>
friend Class &ForEach(Iterator begin, Iterator end, Class &object,
void (Class::*member)(Data &));
...
};
If the function template is defined inside some namespace this namespace
must be mentioned as well. Assuming that ForEach is defined in the
namespace FBB its friend declaration becomes:
template <typename Iterator, typename Class, typename Data>
friend Class &FBB::ForEach(Iterator begin, Iterator end, Class &object,
void (Class::*member)(Data &));
The following example illustrates the use of an unbound friend. The class
Vector2 stores vectors of elements of template type parameter
Type. Its process member allows ForEach to call its private
rows member. The rows member, in turn, uses another ForEach to
call its private columns member. Consequently, Vector2 uses two
instantiations of ForEach which is a clear hint for using an unbound
friend. It is assumed that Type class objects can be inserted into
ostream objects (the definition of the ForEach function template can
be found in the cplusplus.yo.zip archive that can be retrieved from
https://fbb-git.gitlab.io/cppannotations/). Here is the program:
template <typename Type>
class Vector2: public std::vector<std::vector<Type> >
{
using iterator = typename Vector2<Type>::iterator;
template <typename Iterator, typename Class, typename Data>
friend Class &ForEach(Iterator begin, Iterator end, Class &object,
void (Class::*member)(Data &));
public:
void process();
private:
void rows(std::vector<Type> &row);
void columns(Type &str);
};
template <typename Type>
void Vector2<Type>::process()
{
ForEach<iterator, Vector2<Type>, std::vector<Type> >
(this->begin(), this->end(), *this, &Vector2<Type>::rows);
}
template <typename Type>
void Vector2<Type>::rows(std::vector<Type> &row)
{
ForEach(row.begin(), row.end(), *this,
&Vector2<Type>::columns);
std::cout << '\n';
}
template <typename Type>
void Vector2<Type>::columns(Type &str)
{
std::cout << str << " ";
}
using namespace std;
int main()
{
Vector2<string> c;
c.push_back(vector<string>(3, "Hello"));
c.push_back(vector<string>(2, "World"));
c.process();
}
/*
Generated output:
Hello Hello Hello
World World
*/
template <typename Type>
class PtrVector
{
template <typename Iterator, typename Class>
friend class Wrapper; // unbound friend class
};
All members of the class template Wrapper may now instantiate
PtrVectors using any actual type for its Type parameter. This allows
the Wrapper instantiation to access all of PtrVector's private
members.
PtrVector
declares Wrapper::begin as its friend. Note the forward declaration of
the class Wrapper:
template <typename Iterator>
class Wrapper;
template <typename Type>
class PtrVector
{
template <typename Iterator> friend
PtrVector<Type> Wrapper<Iterator>::begin(Iterator const &t1);
...
};
friend makes sense, like int. In those cases the
friend declaration is simply ignored.
Consider the following class template, declaring Friend as a friend:
template <typename Friend>
class Class
{
friend Friend;
void msg(); // private, displays some message
};
Now, an actual Friend class may access all of Class's members
class Concrete
{
Class<Concrete> d_class;
Class<std::string> d_string;
public:
void msg()
{
d_class.msg(); // OK: calls private Class<Concrete>::msg()
//d_string.msg(); // fails to compile: msg() is private
}
};
A declaration like Class<int> intClass is also OK, but here the friend
declaration is simply ignored. After all, there are no `int members' to access
Class<int>'s private members.
Consider the following base class:
template<typename T>
class Base
{
T const &t;
public:
Base(T const &t);
};
The above class is a class template that can be used as a base class for
the following derived class template Derived:
template<typename T>
class Derived: public Base<T>
{
public:
Derived(T const &t);
};
template<typename T>
Derived<T>::Derived(T const &t)
:
Base(t)
{}
Other combinations are also possible. The base class may be instantiated by specifying template arguments, turning the derived class into an ordinary class (showing a class object's definition as well):
class Ordinary: public Base<int>
{
public:
Ordinary(int x);
};
inline Ordinary::Ordinary(int x)
:
Base(x)
{}
Ordinary ordinary{ 5 };
This approach allows us to add functionality to a class template, without the need for constructing a derived class template.
Class template derivation pretty much follows the same rules as ordinary
class derivation, not involving class templates. Some subtleties that are
specific for class template derivation may easily cause confusion like the use
of this when members of a template base class are called from a derived
class. The reasons for using this are discussed in section 23.1. In
the upcoming sections the focus will be on the class derivation proper.
map can
easily be used in combination with the find_if() generic algorithm
(section 19.1.17), it requires the construction of a class and at least
two additional function objects of that class. If this is considered too much
overhead then extending a class template with tailor-made functionality
might be considered.
Example: a program executing commands entered at the keyboard might accept all
unique initial abbreviations of the commands it defines. E.g., the command
list might be entered as l, li, lis or list. By deriving a class
Handler from
map<string, void (Handler::*)(string const &cmd)>
and by defining a member function process(string const &cmd) to do the
actual command processing a program might simply execute the following
main() function:
int main()
{
string line;
Handler cmd;
while (getline(cin, line))
cmd.process(line);
}
The class Handler itself is derived from a std::map, in which
the map's values are pointers to Handler's member functions, expecting the
command line entered by the user. Here are Handler's characteristics:
std::map, expecting the command
associated with each command-processing member as its keys. Since
Handler uses the map merely to define associations between
the commands and the processing
member functions and to make map's types available, private derivation is
used:
class Handler: private std::map<std::string,
void (Handler::*)(std::string const &cmd)>
s_cmds is an array of Handler::value_type values, and
s_cmds_end is a constant pointer pointing beyond the array's last element:
static value_type s_cmds[];
static value_type *const s_cmds_end;
inline Handler::Handler()
:
std::map<std::string,
void (Handler::*)(std::string const &cmd)>
(s_cmds, s_cmds_end)
{}
process iterates along the map's elements. Once the
first word on the command line matches the initial characters of the command,
the corresponding command is executed. If no such command is found, an error
message is issued:
void Handler::process(std::string const &line)
{
istringstream istr(line);
string cmd;
istr >> cmd;
for (iterator it = begin(); it != end(); it++)
{
if (it->first.find(cmd) == 0)
{
(this->*it->second)(line);
return;
}
}
cout << "Unknown command: " << line << '\n';
}
The class template SortVector presented below is derived from the
existing class template std::vector. It allows us to perform a
hierarchic sort of its elements using any ordering of any data members
its data elements may contain. To accomplish this there is but one
requirement. SortVector's data type must offer dedicated member
functions comparing its members.
For example, if SortVector's data type is an object of class
MultiData, then MultiData should implement member functions having the
following prototypes for each of its data members which can be compared:
bool (MultiData::*)(MultiData const &rhv)
So, if MultiData has two data members, int d_value and
std::string d_text and both may be used by a hierarchic sort, then
MultiData should offer the following two members:
bool intCmp(MultiData const &rhv); // returns d_value < rhv.d_value
bool textCmp(MultiData const &rhv); // returns d_text < rhv.d_text
Furthermore, as a convenience it is assumed that operator<< and
operator>> have been defined for MultiData objects.
The class template SortVector is directly derived from the template
class std::vector. Our implementation inherits all members from that base
class. It also offers two simple constructors:
template <typename Type>
class SortVector: public std::vector<Type>
{
public:
SortVector()
{}
SortVector(Type const *begin, Type const *end)
:
std::vector<Type>(begin, end)
{}
Its member hierarchicSort is the true raison d'être for the
class. It defines the hierarchic sort criteria. It expects
a pointer to a series of pointers to member functions of the class
Type as well as a size_t representing the size of the array.
The array's first element indicates Type's most significant sort
criterion, the array's last element indicates the class's least significant
sort criterion. Since the stable_sort generic algorithm was designed
explicitly to support hierarchic sorting, the member uses this generic
algorithm to sort SortVector's elements. With hierarchic sorting, the
least significant criterion should be sorted first. hierarchicSort's
implementation is therefore easy. It requires a support class SortWith
whose objects are initialized by the addresses of the member functions passed
to the hierarchicSort() member:
template <typename Type>
void SortVector<Type>::hierarchicSort(
bool (Type::**arr)(Type const &rhv) const,
size_t n)
{
while (n--)
stable_sort(this->begin(), this->end(), SortWith<Type>(arr[n]));
}
The class SortWith is a simple wrapper class around a pointer to
a predicate function. Since it depends on SortVector's actual data
type the class SortWith must also be a class template:
template <typename Type>
class SortWith
{
bool (Type::*d_ptr)(Type const &rhv) const;
SortWith's constructor receives a pointer to a predicate function and
initializes the class's d_ptr data member:
template <typename Type>
SortWith<Type>::SortWith(bool (Type::*ptr)(Type const &rhv) const)
:
d_ptr(ptr)
{}
Its binary predicate member (operator()) must return true if its
first argument should eventually be placed ahead of its second argument:
template <typename Type>
bool SortWith<Type>::operator()(Type const &lhv, Type const &rhv) const
{
return (lhv.*d_ptr)(rhv);
}
The following examples, which can be embedded in a main
function, provides an illustration:
SortVector object is created for MultiData objects.
It uses the copy generic algorithm to fill the SortVector object from
information appearing at the program's standard input stream. Having
initialized the object its elements are displayed to the standard output
stream:
SortVector<MultiData> sv;
copy(istream_iterator<MultiData>(cin),
istream_iterator<MultiData>(),
back_inserter(sv));
bool (MultiData::*arr[])(MultiData const &rhv) const =
{
&MultiData::textCmp,
&MultiData::intCmp,
};
sv.hierarchicSort(arr, 2);
MultiData's
member functions are swapped, and the previous step is repeated:
swap(arr[0], arr[1]);
sv.hierarchicSort(arr, 2);
echo a 1 b 2 a 2 b 1 | a.out
This results in the following output:
a 1 b 2 a 2 b 1
====
a 1 a 2 b 1 b 2
====
a 1 b 1 a 2 b 2
====
This approach may be used for all class templates having member functions whose implementations do not depend on template parameters. These members may be defined in a separate class which is then used as a base class of the class template derived from it.
As an illustration of this approach we'll develop such a class template
below. We'll develop a class Table derived from an ordinary class
TableType. The class Table displays elements of some type in a
table having a configurable number of columns. The elements are either
displayed horizontally (the first k elements occupy the first row) or
vertically (the first r elements occupy a first column).
When displaying the table's elements they are inserted into a stream. The
table is handled by a separate class (TableType), implementing the table's
presentation. Since the table's elements are inserted into a stream, the
conversion to text (or string) is implemented in Table, but the
handling of the strings themselves is left to TableType. We'll cover some
characteristics of TableType shortly, concentrating on Table's
interface first:
Table is a class template, requiring only one template
type parameter: Iterator referring to an iterator to some data type:
template <typename Iterator>
class Table: public TableType
{
Table doesn't need any data members. All data manipulations are
performed by TableType.
Table has two constructors. The constructor's first two
parameters are Iterators used to iterate over the elements that must be
entered into the table. The constructors require us to specify the number of
columns we would like our table to have as well as a
FillDirection. FillDirection is an enum, defined by TableType,
having values HORIZONTAL and VERTICAL. To allow Table's users to
exercise control over headers, footers, captions, horizontal and vertical
separators, one constructor has a TableSupport reference parameter. The
class TableSupport is developed at a later stage as a virtual class
allowing clients to exercise this control. Here are the class's constructors:
Table(Iterator const &begin, Iterator const &end,
size_t nColumns, FillDirection direction);
Table(Iterator const &begin, Iterator const &end,
TableSupport &tableSupport,
size_t nColumns, FillDirection direction);
Table's only two public members. Both
constructors use a base class initializer to initialize their TableType
base class and then call the class's private member fill to insert data
into the TableType base class object. Here are the constructor's
implementations:
template <typename Iterator>
Table<Iterator>::Table(Iterator const &begin, Iterator const &end,
TableSupport &tableSupport,
size_t nColumns, FillDirection direction)
:
TableType(tableSupport, nColumns, direction)
{
fill(begin, end);
}
template <typename Iterator>
Table<Iterator>::Table(Iterator const &begin, Iterator const &end,
size_t nColumns, FillDirection direction)
:
TableType(nColumns, direction)
{
fill(begin, end);
}
fill member iterates over the range of elements
[begin, end), as defined by the constructor's first two parameters.
As we will see shortly, TableType defines a protected data member
std::vector<std::string> d_string. One of the requirements of the data
type to which the iterators point is that this data type can be inserted into
streams. So, fill uses an ostringstream object to obtain the textual
representation of the data, which is then appended to d_string:
template <typename Iterator>
void Table<Iterator>::fill(Iterator it, Iterator const &end)
{
while (it != end)
{
std::ostringstream str;
str << *it++;
d_string.push_back(str.str());
}
init();
}
This completes the implementation of the class Table. Note that this
class template only has three members, two of them being
constructors. Therefore, in most cases only two function templates must be
instantiated: a constructor and the class's fill member. For example, the
following defines a table having four columns, vertically filled by
strings extracted from the standard input stream:
Table<istream_iterator<string> >
table(istream_iterator<string>(cin), istream_iterator<string>(),
4, TableType::VERTICAL);
The fill-direction is specified as
TableType::VERTICAL. It could also have been specified using Table,
but since Table is a class template its specification would have been
slightly more complex: Table<istream_iterator<string> >::VERTICAL.
Now that the Table derived class has been designed, let's turn our
attention to the class TableType. Here are its essential characteristics:
Table's base
class.
d_colWidth, a
vector storing the width of the widest element per column and d_indexFun,
pointing to the class's member function returning the element in
table[row][column], conditional to the table's fill
direction. TableType also uses a TableSupport pointer and a
reference. The constructor not requiring a TableSupport object uses the
TableSupport * to allocate a (default) TableSupport object and then
uses the TableSupport & as the object's alias. The other constructor
initializes the pointer to 0 and uses the reference data member to refer to
the TableSupport object provided by its parameter. Alternatively, a static
TableSupport object could have been used to initialize the reference data
member in the former constructor. The remaining private data members are
probably self-explanatory:
TableSupport *d_tableSupportPtr;
TableSupport &d_tableSupport;
size_t d_maxWidth;
size_t d_nRows;
size_t d_nColumns;
WidthType d_widthType;
std::vector<size_t> d_colWidth;
size_t (TableType::*d_widthFun)
(size_t col) const;
std::string const &(TableType::*d_indexFun)
(size_t row, size_t col) const;
string objects populating the table are stored in a
protected data member:
std::vector<std::string> d_string;
TableSupport object:
#include "tabletype.ih"
TableType::TableType(TableSupport &tableSupport, size_t nColumns,
FillDirection direction)
:
d_tableSupportPtr(0),
d_tableSupport(tableSupport),
d_maxWidth(0),
d_nRows(0),
d_nColumns(nColumns),
d_widthType(COLUMNWIDTH),
d_colWidth(nColumns),
d_widthFun(&TableType::columnWidth),
d_indexFun(direction == HORIZONTAL ?
&TableType::hIndex
:
&TableType::vIndex)
{}
d_string has been filled, the table is initialized by
Table::fill. The init protected member resizes d_string so
that its size is exactly rows x columns, and it determines the maximum
width of the elements per column. Its implementation is straightforward:
#include "tabletype.ih"
void TableType::init()
{
if (!d_string.size()) // no elements
return; // then do nothing
d_nRows = (d_string.size() + d_nColumns - 1) / d_nColumns;
d_string.resize(d_nRows * d_nColumns); // enforce complete table
// determine max width per column,
// and max column width
for (size_t col = 0; col < d_nColumns; col++)
{
size_t width = 0;
for (size_t row = 0; row < d_nRows; row++)
{
size_t len = stringAt(row, col).length();
if (width < len)
width = len;
}
d_colWidth[col] = width;
if (d_maxWidth < width) // max. width so far.
d_maxWidth = width;
}
}
insert is used by the insertion operator
(operator<<) to insert a Table into a stream. First it informs the
TableSupport object about the table's dimensions. Next it displays the
table, allowing the TableSupport object to write headers, footers and
separators:
#include "tabletype.ih"
ostream &TableType::insert(ostream &ostr) const
{
if (!d_nRows)
return ostr;
d_tableSupport.setParam(ostr, d_nRows, d_colWidth,
d_widthType == EQUALWIDTH ? d_maxWidth : 0);
for (size_t row = 0; row < d_nRows; row++)
{
d_tableSupport.hline(row);
for (size_t col = 0; col < d_nColumns; col++)
{
size_t colwidth = width(col);
d_tableSupport.vline(col);
ostr << setw(colwidth) << stringAt(row, col);
}
d_tableSupport.vline();
}
d_tableSupport.hline();
return ostr;
}
cplusplus.yo.zip archive contains TableSupport's full
implementation. This implementation is found in the directory
yo/classtemplates/examples/table. Most of its remaining members are
private. Among those, these two members return table element
[row][column] for, respectively, a horizontally filled table and a
vertically filled table:
inline std::string const &TableType::hIndex(size_t row, size_t col) const
{
return d_string[row * d_nColumns + col];
}
inline std::string const &TableType::vIndex(size_t row, size_t col) const
{
return d_string[col * d_nRows + row];
}
The support class TableSupport is used to display headers, footers,
captions and separators. It has four virtual members to perform those tasks
(and, of course, a virtual constructor):
hline(size_t rowIndex): called just before displaying
the elements in row
rowIndex.
hline(): called immediately after displaying the final row.
vline(size_t colIndex): called just before displaying the element in
column colIndex.
vline(): called immediately after displaying all elements in a row.
cplusplus.yo.zip archive for the full
implementation of the classes Table, TableType and TableSupport.
Here is a little program showing their use:
/*
table.cc
*/
#include <fstream>
#include <iostream>
#include <string>
#include <iterator>
#include <sstream>
#include "tablesupport/tablesupport.h"
#include "table/table.h"
using namespace std;
using namespace FBB;
int main(int argc, char **argv)
{
size_t nCols = 5;
if (argc > 1)
{
istringstream iss(argv[1]);
iss >> nCols;
}
istream_iterator<string> iter(cin); // first iterator isn't const
Table<istream_iterator<string> >
table(iter, istream_iterator<string>(), nCols,
argc == 2 ? TableType::VERTICAL : TableType::HORIZONTAL);
cout << table << '\n';
}
/*
Example of generated output:
After: echo a b c d e f g h i j | demo 3
a e i
b f j
c g
d h
After: echo a b c d e f g h i j | demo 3 h
a b c
d e f
g h i
j
*/
In many cases, however, dynamic polymorphism isn't really required. Usually
the derived class objects that are passed to functions expecting base class
references are invariants: at fixed locations in programs fixed class types
are used to create objects. The polymorphic nature of these objects is used
inside the functions that receive these objects, expecting references to their
base classes. As an example consider reading information from a network
socket. A class SocketBuffer is derived from std::streambuf, and the
std::stream receiving a pointer to the SocketBuffer merely uses
std::streambuf's interface. However, the implementation, by using
polymorphism, in fact communicates with functions defined in SocketBuffer.
The disadvantages of this scheme are that, firstly, inside the functions expecting references to polymorphic base classes execution is somewhat slowed down precisely because of late-binding. Member functions aren't directly called, but are called indirectly via the object's vpointer and their derived class's Vtable. Secondly, programs using dynamic polymorphism tend to become somewhat bloated compared to programs using static binding. The code bloat is caused by the requirement to satisfy at link-time all the references that are mentioned in all the object files comprising the final program. This requirement forces the linker to link all the functions whose addresses are stored in the Vtables of all polymorphic classes, even if these functions are never actually called.
Static polymorphism allows us to avoid these disadvantages. It can be used instead of dynamic polymorphism in cases where the abovementioned invariant holds. Static polymorphism, also called the curiously recurring template pattern (CRTP), is an example of template meta programming (see also chapter 23 for additional examples of template meta programming).
Whereas dynamic polymorphism is based on the concepts of vpointers, Vtables, and function overriding, static polymorphism capitalizes on the fact that function templates (c.q., member templates) are only compiled into executable code when they are actually called. This allows us to write code in which functions are called which are completely non-existent at the time we write our code. This, however, shouldn't worry us too much. After all, we use a comparable approach when calling a purely virtual function of an abstract base class. The function is really called, but which function is eventually called is determined later in time. With dynamic polymorphism it is determined run-time, with static polymorphism it is determined compile-time.
There's no need to consider static and dynamic polymorphism as mutually exclusive variants of polymorphism. Rather, both can be used together, combining their strengths.
This section contains several subsections.
In the context of dynamic polymorphism these overridable members are the base class's virtual members. In the context of static polymorphism there are no virtual members. Instead, the statically polymorphic base class (referred to as the `base class' below) declares a template type parameter (referred to as the `derived class type' below). Next, the base class's interfacing members call members of the derived class type.
Here is a simple example: a class template acting as a base class. Its public interface consists of one member. But different from dynamic polymorphism there's no reference in the class's interface to any member showing polymorphic behavior (i.e, no `virtual' members are declared):
template <class Derived>
struct Base
{
void interface();
}
Let's have a closer look at the member `interface'. This member is called
by functions receiving a reference or pointer to the base class, but it may
call members that must be available in the derived class type at the point
where interface is called. Before we can call members of the derived class
type an object of the derived class type must be available. This object is
obtained through inheritance. The derived class type is going to be derived
from the base class. Thus Base's this pointer is also Derived's this
pointer.
Forget about polymorphism for a second: when we have a class Derived:
public Base then (because of inheritance) a static_cast<Derived *> can be
used to cast a Base * to a Derived object. A dynamic_cast of
course doesn't apply, as we don't use dynamic polymorphism. But a
static_cast is appropriate since our Base * does in fact point to
a Derived class object.
So, to call a Derived class member from inside interface we
can use the following implementation (remember that Base is a base class
of Derived):
template<class Derived>
void Base<Derived>::interface()
{
static_cast<Derived *>(this)->polymorphic();
}
It's remarkable that, when the compiler is given this implementation it
cannot determine whether Derived is really derived from
Base. Neither can it determine whether the class Derived indeed offers
a member polymorphic. The compiler simply assumes this to be true. If
so, then the provided implementation is syntactically correct. One of the
key characteristics of using templates is that the implementation's viability
is eventually determined at the function's point of instantiation (cf. section
21.6). At that point the compiler will verify that, e.g., the
function polymorphic really is available.
Thus, in order to use the above scheme we must ensure that
polymorphic'.
class First: public Base<First>
In this curious pattern the class First is derived from Base,
which itself is instantiated for First. This is acceptable, as the
compiler already has determined that the type First exists. At this point
that is all it needs.
The second requirement is simply satisfied by defining the member
polymorphic. In chapter 14 we saw that virtual and
overriding members belong to the class's private interface. We can apply the
same philosophy here, by placing polymorphic in First's private
interface, allowing it to be accessed from the base class by declaring
friend void Base<First>::interface();
First's complete class interface can now be designed, followed by
polymorphic's implementation:
class First: public Base<First>
{
friend void Base<First>::interface();
private:
void polymorphic();
};
void First::polymorphic()
{
std::cout << "polymorphic from First\n";
}
Note that the class First itself is not a class template: its members
can be separately compiled and stored in, e.g., a library. Also, as is the
case with dynamic polymorphism, the member polymorphic has full access to
all of First's data members and member functions.
Multiple classes can now be designed like First, each offering their
own implementation of polymorphic. E.g., the member
Second::polymorphic of the class Second, designed like First,
could be implemented like this:
void Second::polymorphic()
{
std::cout << "polymorphic from Second\n";
}
The polymorphic nature of Base becomes apparent once a function
template is defined in which Base::interface is called. Again, the
compiler simply assumes a member interface exists when it reads the
definition of the following function template:
template <class Class>
void fun(Class &object)
{
object.interface();
}
Only where this function is actually called will the compiler verify the
viability of the generated code. In the following main function a
First object is passed to fun: First declares interface
through its base class, and First::polymorphic is called by
interface. The compiler will at this point (i.e., where fun is called)
check whether first indeed has a member polymorphic. Next a Second
object is passed to fun, and here again the compiler checks whether
Second has a member Second::polymorphic:
int main()
{
First first;
fun(first);
Second second;
fun(second);
}
There are also downsides to using static polymorphism:
Second object is passed to fun'
formally isn't correct, since fun is a function template the functions
fun called as fun(first) and fun(second) are
different functions, not just calls of one function with different
arguments. With static polymorphism every instantiation using its own template
parameters results in completely new code which is generated when the template
(e.g., fun) is instantiated. This is something to consider when creating
statically polymorphic base classes. If the base class defines data members
and member functions, and if these additional members are used by derived
class types, then each member has its own instantiation for each derived class
type. This also results in code bloat, albeit of a different kind than
observed with dynamic polymorphism. This kind of code bloat can often be
somewhat reduced by deriving the base class from its own (ordinary,
non-template) base class, encapsulating all elements of the statically
polymorphic base class that do not depend on its template type parameters.
new operator) then the types of the
returned pointers are all different. In addition, the types of the pointers to
their statically polymorphic base classes differ from each other. These
latter pointers are different because they are pointers to Base<Derived>,
representing different types for different Derived types. Consequently,
and different from dynamic polymorphism, these pointers cannot be collected
in, e.g., a vector of shared pointers to base class pointers. There simply
isn't one base class pointer type. Thus, because of the different base class
types, there's no direct statically polymorphic equivalent to virtual
destructors.
In chapter 14 the base class Vehicle and some derived
classes were introduced. Vehicle, Car and Truck's interfaces look like
this (regarding the members that are involved in their polymorphic behaviors):
class Vehicle
{
public:
int mass() const;
private:
virtual int vmass() const;
};
class Car: public Vehicle
{
private:
int vmass() const override;
};
class Truck: public Car
{
private:
int vmass() const override;
};
When converting dynamically polymorphic classes to statically polymorphic classes we must realize that polymorphic classes show two important characteristics:
Vecicle::mass) (i.e., the inheritable
interface), and
Truck::vmass).
With statically polymorphic classes these two characteristics should completely be separated. As we've seen in the previous section, a statically polymorphic derived class derives from its base class by using its own class type as argument to the base class's type parameter. This works fine if there's only one level of inheritance (i.e., one base class, and one or more classes that are directly derived from that base class).
With multiple levels of inheritance (e.g., Truck -> Car -> Vehicle)
Truck's inheritance specification becomes a problem. Here's an intial
attempt to use atatic polymorphism and multiple levels of inheritance:
template <class Derived>
class Vehicle
{
public:
void mass()
{
static_cast<Derived *>(this)->vmass();
}
};
class Car: public Vehicle<Car>
{
friend void Vehicle<Car>::mass();
void vmass();
};
class Truck: public Car
{
void vmass();
};
Truck inherits from Car, then Truck implicitly
derives from Vehicle<Car>, as Car derives from
Vehicle<Car>. Consequently, when Truck{}.mass() is called it is not
Truck::vmass that's activated, but Car's vmass function. But
Truck must derive from Car in order to use Car's protected
features and to add Car's public features to its own public
interface.
Truck from Vehicle<Truck> and from Car
results in a class Truck that also inherits from
Vehicle<Car> (through Truck's Car base class), and compilation fails
as the compiler encounters an ambiguity when instantiating Vehicle::mass:
should it call Class::vmass or should it call Truck::vmass?
Truck{}.mass() calls
Truck::vmass) the redefinable interface must be separated
from the inheritable interface.
In derived classes the protected and public interfaces of (direct or indirect) base classes are made available using standard inheritance. This is shown in the left-hand side of figure 28.

The left-hand side classes are used as base classes for the next level of
inheritance (except for TruckBase, but TruckBase could be used as base
class for yet another level of class inheritance). This line of inheritance
declares the inheritable interface of the classes.
Each of the classes to the left is a base class of a single class to the
right: VehicleBase is a base class for Vehicle, TruckBase for
Truck. The classes to the left contain all members that are completely
independent of the elements that are involved in realizing the static
polymorphism. As that's a mere design principle to realize multiple levels of
static polymorphism the common data hiding principles are relaxed, and the
left-hand side classes declare their matching right-hand side derived class
templates as friend, to allow full access to all members of a left-hand side
class, including the private members, from the matching derived class template
to the right. E.g., VehicleBase declares Vechicle as its friend:
class VehicleBase
{
template <class Derived>
friend class Vehicle;
// all members originally in Vehicle, but not involved
// in realizing static polymorphism are declared here. E.g.,
size_t d_massFactor = 1;
};
The top level class to the left (VehicleBase) lays the foundation of
static polymorphism, by defining that part of the interface that uses the
statically redefinable functions. E.g, using the curiously recurring template
pattern it defines a class member mass that calls the function vmass
of its derived class (in addition it can use all members of its non-class
template base class). E.g,:
template <class Derived>
class Vehicle: public VehicleBase
{
public:
int mass() const
{
return d_massFactor *
static_cast<Derived const *>(this)->vmass();
}
};
Which function actually is called when vmass is called depends on the
implementation in the class Derived, which is handled by the remaining
classes, shown below Vehicle, which are all derived from Vehicle (as
well as from their own ...Base class). These classes use the curiously
recurring template pattern. E.g.,
class Car: public CarBase, public Vehicle<Car>
So, if Car now implements its own vmass function, which can use
any of its own (i.e., CarBase's members), then that function is called
when calling a Vehicle's mass function. E.g.,
template <class Vehicle>
void fun(Vehicle &vehicle)
{
cout << vehicle.mass() << '\n';
}
int main()
{
Car car;
fun(car); // Car's vmass is called
Truck truck;
fun(truck); // Truck's vmass is called
}
Now that we've analyzed the design of statically polymorphic classes using multiple levels of inheritance let's summarize the steps that took to implement static polymorphism
Vehicle. Vehicle's non-redefinable interface is moved
to a class VehicleBase, and Vehicle itself is turned into a statically
polymorphic base class. In general all members of the original
polymorphic base class that do not use or implement virtual members should be
moved to the XBase class.
VehicleBase declares Vehicle to be a friend, to allow
Vehicle full access to its former members, that are now in
VehicleBase.
Vehicle's members refer to the redefinable interface. I.e., its
members call members of its Derived template type parameter. In this
implementation Vehicle does not implement its own vmass member. We
cannot define Vehicle<Vehicle>, and with static polymorphism the base
class is essentially comparable to an abstract base class. If this is
inconvenient then a default class can be specified for Vehicle's Derived
class, implementing the redefinable interface of the original
polymorphic base class (allowing for definitions like Vehicle<> vehicle).
Car moves these members to CarBase and
Truck moves those members to TruckBase.
VehicleBase to
CarBase and from there to TruckBase.
Car and Truck) is a
class template that derives from its base classes, and also, using the
curiously recurrent template pattern, from Vehicle.
Vehicle.
This design pattern can be extended to any level of inheritance: for each
new level a base class is constructed, deriving from the most deeply nested
XXXBase class so far, and deriving from Vehicle<XXX>, implementing its
own ideas about the redefinable interface.
Functions that are used in combination with statically polymorphic classes themselves must be function templates. E.g.,
template <class Vehicle>
void fun(Vehicle &vehicle)
{
cout << vehicle.mass() << '\n';
}
Here, Vehicle is just a formal name. When an object is passed to
fun it must offer a member mass, or compilation will fail. If the
object is in fact a Car or Truck, then their Vehicle<Type> static
base class member mass is called, which in turn uses static polymorphism
to call the member vmass as implemented by the actually passed class
type. The following main function displays, respectively, 1000 and 15000:
int main()
{
Car car;
fun(car);
Truck truck;
fun(truck);
}
Note that this program implements fun twice, rather than once in the
case of dynamic polymorphism. The same holds true for the Vehicle class
template: two implementations, one for the Car type, and one for the
Truck type. The statically polymorphic program will be slightly faster,
though.
(A compilable example using static polymorphism is found in the
C++ Annotations's source distribution's file
yo/classtemplates/examples/staticpolymorphism/polymorph.cc.)
Consider the situation where we have a class containing a container of
pointers to some polymorphic base class type (like the class Vehicle from
chapter 14). How to copy such a container to another container?
We're not hinting at using shared pointers here, but would like to make a full
copy. Clearly, we'll need to duplicate the objects the pointers point at, and
assign these new pointers to the copied object's container.
The prototype design patttern is commonly used to create copies of objects of polymorphic classes, given pointers to their base classes.
To apply the prototype design pattern we have to implement newCopy in all
derived classes. Not by itself a big deal, but static polymorphism can nicely
be used here to avoid having to reimplement this function for each derived
class.
We start off with an abstract base class VehicleBase declaring a pure
virtual member newCopy:
struct VehicleBase
{
virtual ~VehicleBase();
VehicleBase *clone() const; // calls newCopy
// declare any additional members defining the
// public user interface here
private:
VehicleBase *newCopy() const = 0;
};
Next we define a static polymorphic class CloningVehicle which is derived
from VehicleBase (note that we thus combine dynamic and static
polymorphism). This class provides the generic implementation of
newCopy. This is possible because all derived classes can use this
implementation. Also, CloningVehicle will be re-implemented for each
concrete type of vehicle that is eventually used: a Car, a Truck, an
AmphibiousVehicle, etc, etc. CloningVehicle thus isn't shared (like
VehicleBase), but instantiated for each new type of vehicle.
The core characteristic of a statically polymorphic class is that it can use
its class template type parameter via a static_cast of its own type. A
member function like newCopy is implemented always the same way, viz.,
by using the derived class's copy constructor. Here is the class
CloningVehicle:
template <class Derived>
class CloningVehicle: public VehicleBase
{
VehicleBase *newCopy() const
{
return new Derived(*static_cast<Derived const *>(this));
}
};
And we're done. All types of vehicles should now be derived from
CloningVehicle, which automatically provides them with their own
implementation of newCopy. E.g., a class Car looks like this:
class Car: public CloningVehicle<Car>
{
// Car's interface, no need to either
// declare or implement newCopy,
// but a copy constructor is required.
};
Having defined a std::vector<VehicleBase *> original we could create a
copy of original like this:
for(auto pointer: original)
duplicate.push_back(pointer->clone());
Irrespective of the actual type of vehicle to which the pointers point,
their clone members will return pointers to newly allocated copies of
objects of their own types.
PtrVector, a class iterator is defined. The nested class receives its
information from its surrounding class, a PtrVector<Type> class. Since
this surrounding class should be the only class constructing its iterators,
iterator's constructor is made private and the surrounding class is
given access to the private members of iterator using a
bound friend declaration.
Here is the initial section of PtrVector's class interface:
template <typename Type>
class PtrVector: public std::vector<Type *>
This shows that the std::vector base class stores pointers to Type
values, rather than the values themselves. Of course, a destructor is now
required as the (externally allocated) memory for the Type objects must
eventually be freed. Alternatively, the allocation might be part of
PtrVector's tasks, when it stores new elements. Here it is assumed that
PtrVector's clients do the required allocations and that the destructor is
implemented later on.
The nested class defines its constructor as a private member, and allows
PtrVector<Type> objects access to its private members. Therefore only
objects of the surrounding PtrVector<Type> class type are allowed to
construct their iterator objects. However, PtrVector<Type>'s clients
may construct copies of the PtrVector<Type>::iterator objects they
use.
Here is the nested class iterator, using a (required) friend
declaration. Note the use of the typename keyword: since
std::vector<Type *>::iterator depends on a template parameter, it is not
yet an instantiated class. Therefore iterator becomes an implicit
typename. The compiler issues a warning if typename has been
omitted. Here is the class interface:
class iterator
{
friend class PtrVector<Type>;
typename std::vector<Type *>::iterator d_begin;
iterator(PtrVector<Type> &vector);
public:
Type &operator*();
};
The implementation of the members shows that the base class's begin
member is called to initialize d_begin. PtrVector<Type>::begin's
return type must again be preceded by typename:
template <typename Type>
PtrVector<Type>::iterator::iterator(PtrVector<Type> &vector)
:
d_begin(vector.std::vector<Type *>::begin())
{}
template <typename Type>
Type &PtrVector<Type>::iterator::operator*()
{
return **d_begin;
}
The remainder of the class is simple. Omitting all other functions that
might be implemented, the function begin returns a newly constructed
PtrVector<Type>::iterator object. It may call the constructor since the
class iterator declared its surrounding class as its friend:
template <typename Type>
typename PtrVector<Type>::iterator PtrVector<Type>::begin()
{
return iterator(*this);
}
Here is a simple skeleton program, showing how the nested class
iterator might be used:
int main()
{
PtrVector<int> vi;
vi.push_back(new int(1234));
PtrVector<int>::iterator begin = vi.begin();
std::cout << *begin << '\n';
}
Nested enumerations and
nested typedefs and using declarations can also be defined
by class templates. The class Table, mentioned before (section
22.11.3) inherited the enumeration TableType::FillDirection. Had
Table been implemented as a full class template, then this enumeration
would have been defined in Table itself as:
template <typename Iterator>
class Table: public TableType
{
public:
enum FillDirection
{
HORIZONTAL,
VERTICAL
};
...
};
In this case, the actual value of the template type parameter must be
specified when referring to a FillDirection value or to its type. For
example (assuming iter and nCols are defined as in section
22.11.3):
Table<istream_iterator<string> >::FillDirection direction =
argc == 2 ?
Table<istream_iterator<string> >::VERTICAL
:
Table<istream_iterator<string> >::HORIZONTAL;
Table<istream_iterator<string> >
table(iter, istream_iterator<string>(), nCols, direction);
To ensure that an object of a class is interpreted as a particular type of
iterator, the class must be designed so that it satisfies the requirements of
that type of iterator. The interface of a class implementing an iterator uses
iterator_tags, which are available when including the
<iterator> header file.
Iterator classes should provide the following using declarations:
iterator_category, specifying the iterator's tag, as in
using iterator_category = std::random_access_iterator_tag;
differenct_type, defining the type representing differences between
pointers, commonly:
using difference_type = std::ptrdiff_t;
value_type, defining the data type of a dereferenced iterator. E.g.,
using value_type = std::string;
pointer, defining the iterator's pointer type which can also be
defined as a const pointer. E.g.,
using pointer = value_type *; // or maybe:
using pointer = value_type const *;
reference, defining the iterator's pointer type which can also be
defined as a const pointer. E.g.,
using reference = value_type &; // or maybe:
using reference = value_type const &;
These using declarations are commonly encountered in the public sections of iterators, which therefore might be defined as structs. Here's an example of how an iterator's interface could be designed:
struct Iterator
{
using iterator_category = std::random_access_iterator_tag;
using difference_type = std::ptrdiff_t;
using value_type = std::string;
using pointer = value_type *;
using reference = value_type &;
friend bool operator==(iterator const &lhs, iterator const &rhs);
friend auto operator<=>(Iterator const &lhs, Iterator const &rhs);
friend int operator-(Iterator const &lhs, Iterator const &rhs);
friend Iterator operator+(Iterator const &lhs, int step);
friend Iterator operator-(Iterator const &lhs, int step);
private:
// private data members
public:
// public members
private:
// private support members
}
In section 18.2 the characteristics of iterators were
discussed. All iterators
should support (using Iterator as the generic name of the designed
iterator class and Type to represent the (possibly const, in which
case the associated operator should be a const member as well) data type to
which Iterator objects refer):
Iterator &operator++());
Type &operator*());
Type *operator->());
bool operator==(Iterator const &lhs,
Iterator const &rhs), bool operator!=((Iterator const &lhs,
Iterator const &rhs))). Instead of operator!= the `spaceship
operator (operator<=>) can also be used, allowing ordering of the
iterators.
When iterators are used in the context of generic algorithms they must meet additional requirements. These are required because generic algorithms perform checks on the types of the iterators they receive. Simple pointers are usually accepted, but if an iterator-object is used the generic algorithm might require the iterator to specify what type of iterator it represents.
The type of iterator that is implemented is indicated by the class's
iterator_category. The six standard iterator categories are:
std::input_iterator_tag. This tag is used when
the iterator class defines an InputIterator. Iterators of this type allow
reading operations, iterating from the first to the last element of the series
to which the iterator refers.
The InputIterator dereference operator could be declared as follows:
value_type const &operator*() const;or, in a concrete implementation the data type specified at
using
value_type = ... could be used instead to value_type. Except for the
standard operators there are no further requirements for InputIterators.
std::output_iterator_tag. This tag is used when
the iterator class defines an OutputIterator. Iterators of this type allow
assignments to their dereferenced iterators. Therefore, the OutputIterator
dereference operator is usually declared as:
value_type &operator*();Except for the standard operators there are no further requirements for OutputIterators.
std::forward_iterator_tag. This tag is used
when the iterator class defines a ForwardIterator. Iterators of this type
allow reading and assignment operations, iterating from the first to the
last element of the series to which the iterator refers. Therefore, the
ForwardIterator dereference operator should be declared as follows:
value_type &operator*();and it could also declare an overloaded
operator*() const:
value_type const &operator*() const;Except for the standard operators there are no further requirements for ForwardIterators.
std::bidirectional_iterator_tag. This
tag is used when the iterator class defines a
BidirectionalIterator. Iterators of this type allow reading and
assignment operations, iterating step by step, possibly in either direction,
over all elements of the series to which the iterator refers.
The Bidirectional dereference operator should allow assignment to the data its dereference operator refers to and it should allow stepping backward. BidirectionalIterator should therefore, in addition to the standard operators required for iterators, offer the following operators:
value_type &operator*(); // any maybe its const-overload
Iterator &operator--();
std::random_access_iterator_tag. This tag is
used when the iterator class defines a RandomAccessIterator. These
iterators are like Bidirectional iterators, but in addition allow stepping to
the next iterator using int step sizes (the resulting iterator may point
to a location outside of the valid iterator range. Like other iterators,
RandomAccessIterators do not check the validity of the obtained iterator).
In addition to the members offered by the BidirectionalIterator, RandomAccessIterators provide the following operators:
Type operator-(Iterator const &rhs) const, returning the number of
data elements between the current and rhs iterator (returning a negative
value if rhs refers to a data element beyond the data element this
iterator refers to);
Iterator operator+(int step) const, returning an iterator referring
to a data element step data elements beyond the data element this
iterator refers to;
Iterator operator-(int step) const, returning an iterator referring
to a data element step data elements before the data element this
iterator refers to;
bool operator<(Iterator const &rhs) const, returning true if
the data element this iterator refers to is located before the data
element the rhs iterator refers to.
std::contiguous_iterator_tag. This tag is
used when the iterator class defines a ContiguousIterator. These iterators
offer the same facilities as the RandomAccessIterators, but it is the
responsibility of the software engineer to ensure that the elements to which
the iterators refer are stored contiguously in memory.
Each iterator tag assumes that a certain set of operators is
available. The RandomAccessIterators ant ContiguousIterators are the
most complex, as other iterators only offer subsets of their facilities.
Note that iterators are always defined over a certain range
([begin, end)). Increment and decrement operations may result in
undefined behavior of the iterator if the resulting iterator value would refer
to a location outside of this range.
Normally iterators of classes merely accesses the data elements of those classes. Internally, an iterator might use an ordinary pointer but it is hardly ever necessary for the iterator to allocate memory. Therefore, iterators normally don't need to define copy constructors and assignment operators. For the same reason iterators usually don't require destructors.
Most classes offering members returning iterators do so by having members construct the required iterators that are thereupon returned as objects. As the caller of these member functions only has to use or sometimes copy the returned iterator objects, there is usually no need to provide publicly available constructors, except for the copy constructor (which is available by default). Therefore additional constructors are usually defined as private or protected members. To allow an outer class to create iterator objects, the iterator class usually declares the outer class as its friend.
In the following sections a RandomAccessIterator, and a reverse RandomAccessIterator is covered. The container class for which a random access iterator must be developed may actually store its data elements in many different ways (e.g., using containers or pointers to pointers). Section 25.5 contains an example of a self-made template iterator class.
The random access iterator developed in the next sections reaches data elements that are only accessible through pointers. The iterator class is designed as an inner class of a class derived from a vector of string pointers.
unique_ptr and
shared_ptr type objects may be used, though). Although discouraged, we
might be able to use pointer data types in specific contexts. In the following
class StringPtr, an ordinary class is derived from the std::vector
container that uses std::string * as its data type:
This class needs a destructor: as the object stores string pointers, a
destructor is required to destroy the strings once the StringPtr object
itself is destroyed. Similarly, a copy constructor and an overloaded
assignment operator are required. Other members (in particular: constructors)
are not explicitly declared here as they are not relevant to this section's
topic.
Assume that we want to use the sort generic algorithm with
StringPtr objects. This algorithm (see section 19.1.59) requires two
RandomAccessIterators. Although these iterators are available (via
std::vector's begin and end members), they return iterators to
std::string *s. When comparing string * values the pointer values
instead of the content of the strings are compared, which is not what we want.
To remedy this, an internal type StringPtr::iterator is defined,
not returning iterators to pointers, but iterators to the objects these
pointers point to. Once this iterator type is available, we can add the
following members to our StringPtr class interface, hiding the identically
named, but useless members of its base class:
StringPtr::iterator begin(); // returns iterator to the first element
StringPtr::iterator end(); // returns iterator beyond the last
// element
Since these two members return the (proper) iterators, the elements in a
StringPtr object can easily be sorted:
int main()
{
StringPtr sp; // assume sp is somehow filled
sort(sp.begin(), sp.end()); // sp is now sorted
}
To make this work, a type StringPtr::iterator is defined. As suggested by
its type name, iterator is a nested type of StringPtr. To use a
StringPtr::iterator in combination with the sort generic algorithm it
must be a RandomAccessIterator, whose value_type is a
std::string. Therefore, the iterator specifies:
using iterator_category = std::random_access_iterator_tag;
using difference_type = std::ptrdiff_t;
using value_type = std::string;
using pointer = value_type *;
using reference = value_type &;
Now we're ready to redesign StringPtr's class interface. It offers
members returning (reverse) iterators, and a nested iterator class. Here
is its interface:
struct StringPtr: public std::vector<std::string *>
{
class iterator;
using reverse_iterator = std::reverse_iterator<iterator>;
iterator begin();
iterator end();
reverse_iterator rbegin();
reverse_iterator rend();
};
struct StringPtr::iterator
{
//USING
using iterator_category = std::random_access_iterator_tag;
using difference_type = std::ptrdiff_t;
using value_type = std::string;
using pointer = value_type *;
using reference = value_type &;
Next we have a look at StringPtr::iterator's characteristics:
iterator defines StringPtr as its friend, so iterator's
constructor can be private. Only the StringPtr class itself should be able
to construct iterators. Copy construction and iterator-assignment should be
possible, but that's possible by default and needs no specific declaration or
implementation. Furthermore, since an iterator is already provided by
StringPtr's base class, we can use that iterator to access the information
stored in the StringPtr object.
StringPtr::begin and StringPtr::end may simply return
iterator objects. They are implemented like this:
inline StringPtr::iterator StringPtr::begin()
{
return iterator(std::vector<std::string *>::begin());
}
inline StringPtr::iterator StringPtr::end()
{
return iterator(std::vector<std::string *>::end());
}
iterator's remaining members are public. It's very easy to
implement them, mainly manipulating and dereferencing the available iterator
d_current. A RandomAccessIterator requires a series of operators. They
usually have very simple implementations, and can often very well be
implemented inline:
iterator &operator++(); the pre-increment operator:
inline StringPtr::iterator &StringPtr::iterator::operator++()
{
++d_current;
return *this;
}
iterator operator++(int); the post-increment operator:
inline StringPtr::iterator StringPtr::iterator::operator++(int)
{
return iterator(d_current++);
}
iterator &operator--(); the pre-decrement operator:
inline StringPtr::iterator &StringPtr::iterator::operator--()
{
--d_current;
return *this;
}
iterator operator--(int); the post-decrement operator:
inline StringPtr::iterator StringPtr::iterator::operator--(int)
{
return iterator(d_current--);
}
iterator &operator=(iterator const &other); the overloaded
assignment operator. Since iterator objects do not allocate
any memory themselves, the default assignment operator can be
used.
bool operator==(iterator const &rhv) const; testing the equality
of two iterator objects:
inline bool operator==(StringPtr::iterator const &lhs,
StringPtr::iterator const &rhs)
{
return lhs.d_current == rhs.d_current;
}
autol operator<=>(iterator const &rhv) const; comparing
two iterator objects:
inline auto operator<=>(StringPtr::iterator const &lhs,
StringPtr::iterator const &rhs)
{
return lhs.d_current <=> rhs.d_current;
}
int operator-(iterator const &rhv) const; returning the number of
elements between the element pointed to by the left-hand side
iterator and the right-hand side iterator (i.e., the value to add
to the left-hand side iterator to make it equal to the value of
the right-hand side iterator):
inline int operator-(StringPtr::iterator const &lhs,
StringPtr::iterator const &rhs)
{
return lhs.d_current - rhs.d_current;
}
Type &operator*() const; returning a reference to the object to
which the current iterator points. With an InputIterator and
with all const_iterators, the return type of this overloaded
operator should be Type const &. This operator returns a
reference to a string. This string is obtained by dereferencing
the dereferenced d_current value. As d_current is an
iterator to string * elements, two dereference operations are
required to reach the string itself:
inline std::string &StringPtr::iterator::operator*() const
{
return **d_current;
}
iterator operator+(int stepsize) const; this operator
advances the current iterator by stepsize:
inline StringPtr::iterator operator+(StringPtr::iterator const &lhs,
int step)
{
StringPtr::iterator ret{ lhs };
ret.d_current += step; // avoids ambiguity
return ret;
}
iterator operator-(int stepsize) const; this operator
decreases the current iterator by stepsize:
inline StringPtr::iterator operator-(StringPtr::iterator const &lhs,
int step)
{
StringPtr::iterator ret{ lhs };
ret.d_current -= step; // avoids ambiguity
return ret;
}
std::string *operator->() const is an additionally added
operator. Here only one dereference operation is required,
returning a pointer to the string, allowing us to access the
members of a string via its pointer.
inline std::string *StringPtr::iterator::operator->() const
{
return *d_current;
}
operator+= and
operator-=. They are not formally required by
RandomAccessIterators, but they come in handy anyway:
inline StringPtr::iterator &StringPtr::iterator::operator+=(int step)
{
d_current += step;
return *this;
}
inline StringPtr::iterator &StringPtr::iterator::operator-=(int step)
{
d_current -= step;
return *this;
}
operator+(int step) can be omitted from the interface. Of course, the tag
to use would then be std::forward_iterator_tag. The tags (and the set of
required operators) vary accordingly for the other iterator types.
std::reverse_iterator is used, which nicely
implements the reverse iterator once we have defined an iterator. Its
constructor merely requires an object of the iterator type for which we want
to construct a reverse iterator.
To implement a reverse iterator for StringPtr we only need to define
the reverse_iterator type in its interface. This requires us to specify
only one line of code, which must be inserted after the interface of the class
iterator:
using reverse_iterator = std::reverse_iterator<iterator>;
Also, the well known members rbegin and rend are added to
StringPtr's interface. Again, they can easily be implemented inline:
inline StringPtr::reverse_iterator StringPtr::rbegin()
{
return reverse_iterator(end());
}
inline StringPtr::reverse_iterator StringPtr::rend()
{
return reverse_iterator(begin());
}
Note the arguments the reverse_iterator constructors receive: the
begin point of the reversed iterator is obtained by providing
reverse_iterator's constructor with the value returned by the member
end: the endpoint of the normal iterator range; the endpoint of
the reversed iterator is obtained by providing reverse_iterator's
constructor with the value returned by the member begin: the begin
point of the normal iterator range.
The following program illustrates the use of StringPtr's
RandomAccessIterator:
#include <iostream>
#include <algorithm>
#include "stringptr.h"
using namespace std;
int main(int argc, char **argv)
{
StringPtr sp;
while (*argv)
sp.push_back(new string{ *argv++ });
sort(sp.begin(), sp.end());
copy(sp.begin(), sp.end(), ostream_iterator<string>(cout, " "));
cout << "\n======\n";
sort(sp.rbegin(), sp.rend());
copy(sp.begin(), sp.end(), ostream_iterator<string>(cout, " "));
cout << '\n';
}
/*
when called as:
a.out bravo mike charlie zulu quebec
generated output:
a.out bravo charlie mike quebec zulu
======
zulu quebec mike charlie bravo a.out
*/
Although it is thus possible to construct a reverse iterator from a normal
iterator, the opposite does not hold true: it is not possible to
initialize a normal iterator from a reverse iterator.
Assume we would like to process all lines stored in vector<string>
lines up to any trailing empty lines (or lines only containing blanks) it
might contain. How should we proceed? One approach is to start the processing
from the first line in the vector, continuing until the first of the trailing
empty lines. However, once we encounter an empty line it does of course not
have to be the first line of the set of trailing empty lines. In that case,
we'd better use the following algorithm:
rit = find_if(lines.rbegin(), lines.rend(), NonEmpty());
to obtain a reverse_iterator rit pointing to the last non-empty
line.
for_each(lines.begin(), --rit, Process());
to process all lines up to the first empty line.
reverse_iterator? The solution is not very difficult, as an iterator may
be initialized from a pointer. Although the reverse iterator rit is not a
pointer, &*(rit - 1) or &*--rit is. So we use
for_each(lines.begin(), &*--rit, Process());to process all the lines up to the first of the set of trailing empty lines. In general, if
rit is a reverse_iterator pointing to some
element and we need an iterator to point to that element, we may use
&*rit to initialize the iterator. Here, the dereference operator is
applied to reach the element the reverse iterator refers to. Then the address
operator is applied to obtain its address with which we can initialize the
iterator.
When defining a const_reverse_iterator (e.g., matching a
const_iterator class), then the const_iterator's operator* member
should be a member returning a non-modifiable value or object. Since a
const_reverse_iterator uses the iterator's operator-- member,
we're running against a small conceptual conflict. On the one hand, a
std::input_iterator_tag is inappropriate, since we must allow decrementing
the iterator. On the other hand, a std::bidirectional_iterator is
inappropriate, since we don't allow modification of the data.
Iterator tags are primarily conceptual. If const_iterators and
const_reverse_iterators only allow increment operations, then an
input_iterator_tag is the best match for the iterator's intended
use. Hence this tag is used below.
Furthermore, in line with the nature of a input_iterator_tag our
const_iterator should not offer an operator--. This, of course,
causes problems: a reverse iterator must be able to use the iterator's
operator-- member. This can easily be solved by stashing the iterator's
operator-- in the iterator's private section, and declaring
std::reverse_iterator<(const_)iterator> its friend (note that declaring a
(const_)reverse_iterator that is derived from std::reverse_iterator
doesn't solve the issue: it is std::reverse_iterator that calls the
iterator's operator--, not a class that is derived from it).
To keep the const-ness of dereferencing const_iterator iterators
using specification can added to the const_iterator class. The
using specifications provided by Data::iterator are inherited by
Data::const_iterator, but Data::const_iterator may also specify:
using const_pointer = value_type const *;
using const_reference = value_type const &;
whereafter its operator *() can return a const_reference.
The elements involved in defining an iterator, const_iterator,
reverse_iterator and const_reverse_iterator for a class Data is
illustrated in the following example, which only requires the definitions of
the iterator and const_iterator classes, as these types can be passed
to the reverse_iterator template to obtain the corresponding
reverse-iterators:
// compile only: members only declared, not implemented
#include <string>
#include <iterator>
#include <iostream>
struct Data
{
class iterator;
class const_iterator;
using reverse_iterator = std::reverse_iterator<iterator>;
using const_reverse_iterator = std::reverse_iterator<const_iterator>;
private:
std::string *d_data;
size_t d_n;
public:
// ...
};
struct Data::iterator
{
using iterator_category = std::bidirectional_iterator_tag;
using difference_type = std::ptrdiff_t;
using value_type = std::string;
using pointer = value_type *;
using reference = value_type &;
friend class Data;
iterator() = default;
iterator &operator++();
iterator &operator--();
std::string &operator*();
private:
iterator(std::string *data, size_t idx);
friend class std::reverse_iterator<iterator>;
};
bool operator==(Data::iterator const &lhs, Data::iterator const &rhs);
struct Data::const_iterator: public Data::iterator
{
using const_pointer = value_type const *;
using const_reference = value_type const &;
friend class Data;
friend class std::reverse_iterator<const_iterator>;
const_iterator() = default;
const_iterator &operator++();
const_iterator &operator--();
const_reference operator*() const;
// or, in this case: std::string const &operator*() const;
private:
const_iterator(std::string const *data, size_t idx);
};
bool operator==(Data::const_iterator const &lhs,
Data::const_iterator const &rhs);
void demo()
{
Data::iterator iter;
Data::reverse_iterator riter(iter);
std::cout << *riter << '\n';
Data::const_iterator citer;
Data::const_reverse_iterator criter(citer);
std::cout << *criter << '\n';
};