Composable cycles¶
- Version
0.11.0
- Date
Nov 04, 2021
Docs |
|
PyPI |
|
GitHub |
cycler API¶
|
Create a new |
|
Composable cycles. |
|
Concatenate |
The public API of cycler consists of a class Cycler, a
factory function cycler(), and a concatenation function
concat(). The factory function provides a simple interface for
creating ‘base’ Cycler objects while the class takes care of the
composition and iteration logic.
Cycler Usage¶
Base¶
A single entry Cycler object can be used to easily
cycle over a single style. To create the Cycler use the cycler()
function to link a key/style/kwarg to series of values. The key must be
hashable (as it will eventually be used as the key in a dict).
In [1]: from __future__ import print_function
In [2]: from cycler import cycler
In [3]: color_cycle = cycler(color=['r', 'g', 'b'])
In [4]: color_cycle
Out[4]: cycler('color', ['r', 'g', 'b'])
The Cycler knows it’s length and keys:
In [5]: len(color_cycle)
Out[5]: 3
In [6]: color_cycle.keys
Out[6]: {'color'}
Iterating over this object will yield a series of dict objects keyed on
the label
In [7]: for v in color_cycle:
...: print(v)
...:
{'color': 'r'}
{'color': 'g'}
{'color': 'b'}
Cycler objects can be passed as the argument to cycler()
which returns a new Cycler with a new label, but the same values.
In [8]: cycler(ec=color_cycle)
Out[8]: cycler('ec', ['r', 'g', 'b'])
Iterating over a Cycler results in the finite list of entries, to
get an infinite cycle, call the Cycler object (a-la a generator)
In [9]: cc = color_cycle()
In [10]: for j, c in zip(range(5), cc):
....: print(j, c)
....:
0 {'color': 'r'}
1 {'color': 'g'}
2 {'color': 'b'}
3 {'color': 'r'}
4 {'color': 'g'}
Composition¶
A single Cycler can just as easily be replaced by a single for
loop. The power of Cycler objects is that they can be composed to easily
create complex multi-key cycles.
Addition¶
Equal length Cycler s with different keys can be added to get the
‘inner’ product of two cycles
In [11]: lw_cycle = cycler(lw=range(1, 4))
In [12]: wc = lw_cycle + color_cycle
The result has the same length and has keys which are the union of the
two input Cycler’s.
In [13]: len(wc)
Out[13]: 3
In [14]: wc.keys
Out[14]: {'color', 'lw'}
and iterating over the result is the zip of the two input cycles
In [15]: for s in wc:
....: print(s)
....:
{'lw': 1, 'color': 'r'}
{'lw': 2, 'color': 'g'}
{'lw': 3, 'color': 'b'}
As with arithmetic, addition is commutative
In [16]: lw_c = lw_cycle + color_cycle
In [17]: c_lw = color_cycle + lw_cycle
In [18]: for j, (a, b) in enumerate(zip(lw_c, c_lw)):
....: print('({j}) A: {A!r} B: {B!r}'.format(j=j, A=a, B=b))
....:
(0) A: {'lw': 1, 'color': 'r'} B: {'color': 'r', 'lw': 1}
(1) A: {'lw': 2, 'color': 'g'} B: {'color': 'g', 'lw': 2}
(2) A: {'lw': 3, 'color': 'b'} B: {'color': 'b', 'lw': 3}
For convenience, the cycler() function can have multiple
key-value pairs and will automatically compose them into a single
Cycler via addition
In [19]: wc = cycler(c=['r', 'g', 'b'], lw=range(3))
In [20]: for s in wc:
....: print(s)
....:
{'c': 'r', 'lw': 0}
{'c': 'g', 'lw': 1}
{'c': 'b', 'lw': 2}
Multiplication¶
Any pair of Cycler can be multiplied
In [21]: m_cycle = cycler(marker=['s', 'o'])
In [22]: m_c = m_cycle * color_cycle
which gives the ‘outer product’ of the two cycles (same as
itertools.product() )
In [23]: len(m_c)
Out[23]: 6
In [24]: m_c.keys
Out[24]: {'color', 'marker'}
In [25]: for s in m_c:
....: print(s)
....:
{'marker': 's', 'color': 'r'}
{'marker': 's', 'color': 'g'}
{'marker': 's', 'color': 'b'}
{'marker': 'o', 'color': 'r'}
{'marker': 'o', 'color': 'g'}
{'marker': 'o', 'color': 'b'}
Note that unlike addition, multiplication is not commutative (like matrices)
In [26]: c_m = color_cycle * m_cycle
In [27]: for j, (a, b) in enumerate(zip(c_m, m_c)):
....: print('({j}) A: {A!r} B: {B!r}'.format(j=j, A=a, B=b))
....:
(0) A: {'color': 'r', 'marker': 's'} B: {'marker': 's', 'color': 'r'}
(1) A: {'color': 'r', 'marker': 'o'} B: {'marker': 's', 'color': 'g'}
(2) A: {'color': 'g', 'marker': 's'} B: {'marker': 's', 'color': 'b'}
(3) A: {'color': 'g', 'marker': 'o'} B: {'marker': 'o', 'color': 'r'}
(4) A: {'color': 'b', 'marker': 's'} B: {'marker': 'o', 'color': 'g'}
(5) A: {'color': 'b', 'marker': 'o'} B: {'marker': 'o', 'color': 'b'}
Integer Multiplication¶
Cycler s can also be multiplied by integer values to increase the length.
In [28]: color_cycle * 2
Out[28]: cycler('color', ['r', 'g', 'b', 'r', 'g', 'b'])
In [29]: 2 * color_cycle
Out[29]: cycler('color', ['r', 'g', 'b', 'r', 'g', 'b'])
Concatenation¶
Cycler objects can be concatenated either via the Cycler.concat() method
In [30]: color_cycle.concat(color_cycle)
Out[30]: cycler('color', ['r', 'g', 'b', 'r', 'g', 'b'])
or the top-level concat() function
In [31]: from cycler import concat
In [32]: concat(color_cycle, color_cycle)
Out[32]: cycler('color', ['r', 'g', 'b', 'r', 'g', 'b'])
Slicing¶
Cycles can be sliced with slice objects
In [33]: color_cycle[::-1]
Out[33]: cycler('color', ['b', 'g', 'r'])
In [34]: color_cycle[:2]
Out[34]: cycler('color', ['r', 'g'])
In [35]: color_cycle[1:]
Out[35]: cycler('color', ['g', 'b'])
to return a sub-set of the cycle as a new Cycler.
Inspecting the Cycler¶
To inspect the values of the transposed Cycler use
the Cycler.by_key method:
In [36]: c_m.by_key()
Out[36]:
{'marker': ['s', 'o', 's', 'o', 's', 'o'],
'color': ['r', 'r', 'g', 'g', 'b', 'b']}
This dict can be mutated and used to create a new Cycler with
the updated values
In [37]: bk = c_m.by_key()
In [38]: bk['color'] = ['green'] * len(c_m)
In [39]: cycler(**bk)
Out[39]: (cycler('marker', ['s', 'o', 's', 'o', 's', 'o']) + cycler('color', ['green', 'green', 'green', 'green', 'green', 'green']))
Examples¶
We can use Cycler instances to cycle over one or more kwarg to
plot :
from cycler import cycler
from itertools import cycle
fig, (ax1, ax2) = plt.subplots(1, 2, tight_layout=True,
figsize=(8, 4))
x = np.arange(10)
color_cycle = cycler(c=['r', 'g', 'b'])
for i, sty in enumerate(color_cycle):
ax1.plot(x, x*(i+1), **sty)
for i, sty in zip(range(1, 5), cycle(color_cycle)):
ax2.plot(x, x*i, **sty)
(Source code, png, hires.png, pdf)
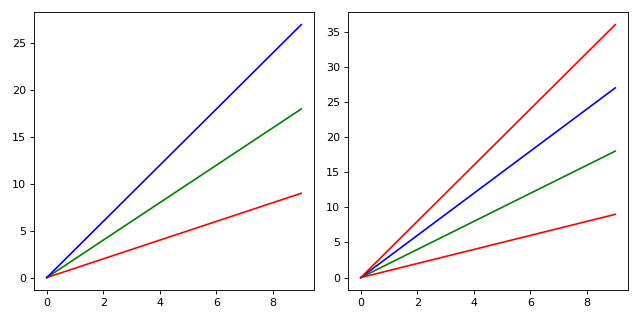
from cycler import cycler
from itertools import cycle
fig, (ax1, ax2) = plt.subplots(1, 2, tight_layout=True,
figsize=(8, 4))
x = np.arange(10)
color_cycle = cycler(c=['r', 'g', 'b'])
ls_cycle = cycler('ls', ['-', '--'])
lw_cycle = cycler('lw', range(1, 4))
sty_cycle = ls_cycle * (color_cycle + lw_cycle)
for i, sty in enumerate(sty_cycle):
ax1.plot(x, x*(i+1), **sty)
sty_cycle = (color_cycle + lw_cycle) * ls_cycle
for i, sty in enumerate(sty_cycle):
ax2.plot(x, x*(i+1), **sty)
(Source code, png, hires.png, pdf)
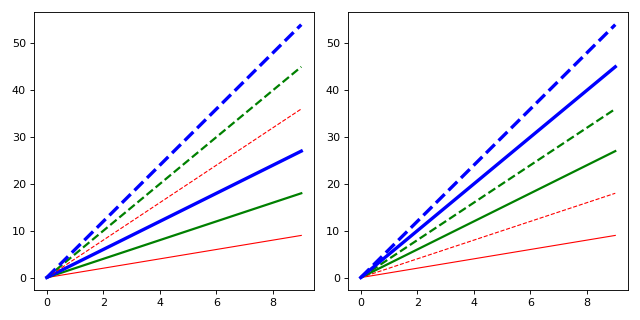
Persistent Cycles¶
It can be useful to associate a given label with a style via
dictionary lookup and to dynamically generate that mapping. This
can easily be accomplished using a defaultdict
In [40]: from cycler import cycler as cy
In [41]: from collections import defaultdict
In [42]: cyl = cy('c', 'rgb') + cy('lw', range(1, 4))
To get a finite set of styles
In [43]: finite_cy_iter = iter(cyl)
In [44]: dd_finite = defaultdict(lambda : next(finite_cy_iter))
or repeating
In [45]: loop_cy_iter = cyl()
In [46]: dd_loop = defaultdict(lambda : next(loop_cy_iter))
This can be helpful when plotting complex data which has both a classification and a label
finite_cy_iter = iter(cyl)
styles = defaultdict(lambda : next(finite_cy_iter))
for group, label, data in DataSet:
ax.plot(data, label=label, **styles[group])
which will result in every data with the same group being plotted with
the same style.
Exceptions¶
A ValueError is raised if unequal length Cycler s are added together
In [47]: cycler(c=['r', 'g', 'b']) + cycler(ls=['-', '--'])
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-47-8d89d25d1b2f> in <module>
----> 1 cycler(c=['r', 'g', 'b']) + cycler(ls=['-', '--'])
/build/python-cycler-QRjsEH/python-cycler-0.11.0/.pybuild/cpython3_3.9_cycler/build/cycler.py in __add__(self, other)
257 """
258 if len(self) != len(other):
--> 259 raise ValueError("Can only add equal length cycles, "
260 f"not {len(self)} and {len(other)}")
261 return Cycler(self, other, zip)
ValueError: Can only add equal length cycles, not 3 and 2
or if two cycles which have overlapping keys are composed
In [48]: color_cycle = cycler(c=['r', 'g', 'b'])
In [49]: color_cycle + color_cycle
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-49-c3f07b28cc3d> in <module>
----> 1 color_cycle + color_cycle
/build/python-cycler-QRjsEH/python-cycler-0.11.0/.pybuild/cpython3_3.9_cycler/build/cycler.py in __add__(self, other)
259 raise ValueError("Can only add equal length cycles, "
260 f"not {len(self)} and {len(other)}")
--> 261 return Cycler(self, other, zip)
262
263 def __mul__(self, other):
/build/python-cycler-QRjsEH/python-cycler-0.11.0/.pybuild/cpython3_3.9_cycler/build/cycler.py in __init__(self, left, right, op)
157 self._right = None
158
--> 159 self._keys = _process_keys(self._left, self._right)
160 self._op = op
161
/build/python-cycler-QRjsEH/python-cycler-0.11.0/.pybuild/cpython3_3.9_cycler/build/cycler.py in _process_keys(left, right)
69 r_key = set(r_peek.keys())
70 if l_key & r_key:
---> 71 raise ValueError("Can not compose overlapping cycles")
72 return l_key | r_key
73
ValueError: Can not compose overlapping cycles
Motivation¶
When plotting more than one line it is common to want to be able to cycle over one or more artist styles. For simple cases than can be done with out too much trouble:
fig, ax = plt.subplots(tight_layout=True)
x = np.linspace(0, 2*np.pi, 1024)
for i, (lw, c) in enumerate(zip(range(4), ['r', 'g', 'b', 'k'])):
ax.plot(x, np.sin(x - i * np.pi / 4),
label=r'$\phi = {{{0}}} \pi / 4$'.format(i),
lw=lw + 1,
c=c)
ax.set_xlim([0, 2*np.pi])
ax.set_title(r'$y=\sin(\theta + \phi)$')
ax.set_ylabel(r'[arb]')
ax.set_xlabel(r'$\theta$ [rad]')
ax.legend(loc=0)
(Source code, png, hires.png, pdf)
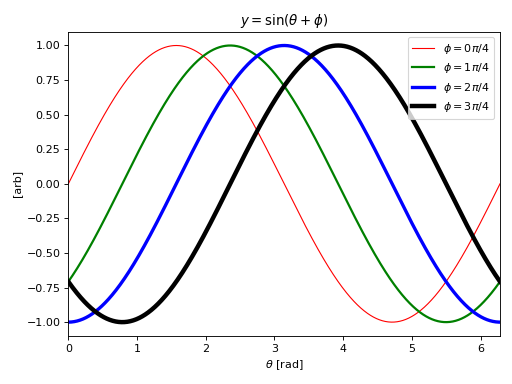
However, if you want to do something more complicated:
fig, ax = plt.subplots(tight_layout=True)
x = np.linspace(0, 2*np.pi, 1024)
for i, (lw, c) in enumerate(zip(range(4), ['r', 'g', 'b', 'k'])):
if i % 2:
ls = '-'
else:
ls = '--'
ax.plot(x, np.sin(x - i * np.pi / 4),
label=r'$\phi = {{{0}}} \pi / 4$'.format(i),
lw=lw + 1,
c=c,
ls=ls)
ax.set_xlim([0, 2*np.pi])
ax.set_title(r'$y=\sin(\theta + \phi)$')
ax.set_ylabel(r'[arb]')
ax.set_xlabel(r'$\theta$ [rad]')
ax.legend(loc=0)
(Source code, png, hires.png, pdf)
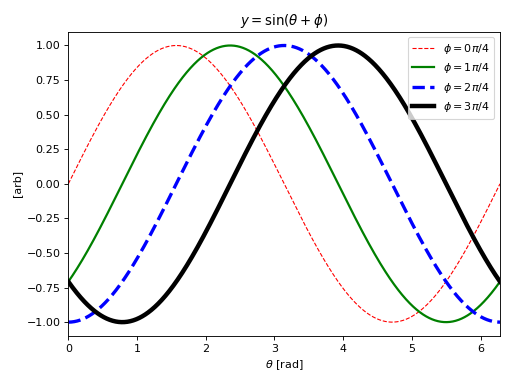
the plotting logic can quickly become very involved. To address this and allow easy
cycling over arbitrary kwargs the Cycler class, a composable
kwarg iterator, was developed.