The interesting part is that the kind of data that can be stored inside these containers has been left unspecified at the time the containers were constructed. That's why they are spoken of as abstract containers.
Abstract containers rely heavily on templates, covered in chapter
21 and beyond. To use abstract containers, only a minimal grasp of
the template concept is required. In C++ a template is in fact a recipe
for constructing a function or a complete class. The recipe tries to abstract
the functionality of the class or function as much as possible from the data
on which the class or function operates. As the data types on which the
templates operate were not known when the template was implemented, the
datatypes are either inferred from the context in which a function template is
used, or they are mentioned explicitly when a class template is used (the term
that's used here is instantiated). In situations where the types are
explicitly mentioned, the angle bracket notation is used to indicate
which data types are required. For example, below (in section 12.2) we'll
encounter the pair container, which requires the
explicit mentioning of two data types. Here is a pair object
containing both an int and a string:
pair<int, string> myPair;
The object myPair is defined as an object holding both an int and
a string.
The angle bracket notation is used intensively in the upcoming discussion of abstract containers. Actually, understanding this part of templates is the only real requirement for using abstract containers. Now that we've introduced this notation, we can postpone the more thorough discussion of templates to chapter 21, and concentrate on their use in this chapter.
Most abstract containers are sequential containers: they contain
data that can be stored and retrieved in some sequential
way. Examples are the array, implementing a fixed-sized array; a
vector, implementing an extendable array; the
list, implementing a data structure that allows for the easy insertion or
deletion of data; the queue, also called a FIFO
(first in, first out) structure, in which the first element that is
entered is the first element to be retrieved again; and the stack,
which is a
first in, last out (FILO or LIFO) structure.
In addition to sequential containers several special containers are
available. The pair is a basic container in which a pair of values (of
types that are left open for further specification) can be stored, like two
strings, two ints, a string and a double, etc.. Pairs are often used to return
data elements that naturally come in pairs. For example, the map is an
abstract container storing keys and their associated values. Elements
of these maps are returned as pairs.
A variant of the pair is the complex container, implementing
operations that are defined on complex numbers.
A tuple (cf. section 22.6) generalizes the pair container to a
data structure accommodating any number of different data types.
All abstract containers described in this chapter as well as the string
and stream datatypes (cf. chapters 5 and 6) are part of
the Standard Template Library.
All but the unordered containers support the following basic set of operators:
== and !=
The equality operator applied to two containers returns true if the two
containers have the same number of elements, which are pairwise equal
according to the equality operator of the contained data type. The
inequality operator does the opposite;
<, <=, > and
>=. The < operator returns true if each element in the
left-hand side container is less than each corresponding element in the
right-hand side container. Additional elements in either the left-hand side
container or the right-hand side container are ignored.
container left;
container right;
left = {0, 2, 4};
right = {1, 3}; // left < right
right = {1, 3, 6, 1, 2}; // left < right
class-type) can be stored in a container, the
user-defined type should at least support:
Sequential containers can also be initialized using initializer lists.
Most containers (exceptions are the stack (section 12.3.11), priority_queue (section 12.3.5), and queue (section 12.3.4) containers) support members to determine their maximum sizes (through their member function max_size).
Virtually all containers support copy construction. If the container supports copy construction and the container's data type supports move construction, then move construction is automatically used for the container's data elements when a container is initialized with an anonymous temporary container.
Closely linked to the standard template library are the
generic algorithms. These algorithms may be used to perform
frequently occurring tasks or more complex tasks than is possible with the
containers themselves, like counting, filling, merging, filtering etc.. An
overview of generic algorithms and their applications is given in chapter
19. Generic algorithms usually rely on the availability of
iterators, representing begin and
end-points for processing data stored inside containers. The abstract
containers usually support constructors and members expecting iterators, and
they often have members returning iterators (comparable to the
string::begin and string::end members). In this chapter the
iterator concept is not further investigated. Refer to chapter 18 for
this.
Containers often collect data during their lifetimes. When a container
goes out of scope, its destructor tries to destroy its data elements. This
only succeeds if the data elements themselves are stored inside the
container. If the data elements of containers
are pointers to dynamically allocated memory then the memory pointed to by
these pointers is not destroyed, resulting in a memory leak. A consequence
of this scheme is that the data stored in a container should often be
considered the `property' of the container: the container should be able to
destroy its data elements when the container's destructor is called. So,
normally containers should not contain pointers to data. Also, a container
should not be required
to contain const data, as const data
prevent the use of many of the container's members, like the assignment
operator.
std:: is usually omitted.
pair may represent pair<string,
int>.
Type represents the generic type. Type could
be int, string, etc.
object and container represent objects of the
container type under discussion.
value represents a value of the type that is
stored in the container.
n represent unsigned
values.
pos, from, beyond
map container, contain pairs of
values, usually called `keys' and `values'. For such containers the following
notational convention is used in addition:
key indicates a value of the used key-type
keyvalue indicates a value of the `value_type'
used with the particular container.
pair container is a rather basic container. It is
used to store two elements, called first and second, and that's about
it. Before using pair containers the header file <utility> must be
included.
The pair's data types are specified when the pair object is
defined (or declared) using the template's angle bracket notation (cf. chapter
21). Examples:
pair<string, string> piper("PA28", "PH-ANI");
pair<string, string> cessna("C172", "PH-ANG");
here, the variables piper and cessna are defined as pair
variables containing two strings. Both strings can be retrieved using the
first and second fields of the pair type:
cout << piper.first << '\n' << // shows 'PA28'
cessna.second << '\n'; // shows 'PH-ANG'
The first and second members can also be used to reassign values:
cessna.first = "C152";
cessna.second = "PH-ANW";
If a pair object must be completely reassigned, an anonymous
pair object can be used as the right-hand operand of
the assignment. An anonymous variable defines a temporary variable (which
receives no name) solely for the purpose of (re)assigning another variable of
the same type. Its generic form is
type(initializer list)
Note that when a pair object is used the type specification is not
completed by just mentioning the containername pair. It also requires the
specification of the data types which are stored within the pair. For this the
(template) angle bracket notation is used again. E.g., the reassignment
of the cessna pair variable could have been accomplished as follows:
cessna = pair<string, string>("C152", "PH-ANW");
In cases like these, the type specification can become quite
elaborate, in which case using declarations can be used to improve
readability. If many pair<type1, type2> clauses are
used in a source, the typing effort may be reduced and readability might be
improved by first defining a name for the clause, and then using the defined
name later. E.g.,
using pairStrStr = pair<string, string>;
cessna = pairStrStr("C152", "PH-ANW");
All abstract containers are class templates, and the types for which class templates are initialized are commonly specified between pointed brackets following the class template's name. However, the compiler may be able to deduce the container's types from the types of arguments that are specified when constructing the container. E.g., when defining
pair values{ 1, 1.5 };
the compiler deduces that values.first is an int and
values.second is a double. Sometimes the class template's types cannot
be deduced. In those cases the intended types must explicitly be specified:
pair<int, double> values;
Although the compiler will deduce types whenever it can, it might not deduce the types we had in mind. Had we defined
pair cessna{ "C172", "PH-BVL" };
then the compilation would succeed, but an expression like
cout << cessna.first.length() would not compile, as "C172" is
a NTBS, and hence cessna.first is a char *. In this case simply
appending an s to the NTBSs fixes the problem, but such a simple fix might
not always be available. Section 12.3.2 has contains more information
about deducing template parameter types.
Apart from this (and the basic set of operations (assignment and
comparisons)) the pair offers no further functionality. It is, however,
a basic ingredient of the upcoming abstract containers map, multimap and
hash_map.
C++ also offers a generalized pair container: the tuple, covered in section 22.6.
array class implements a
fixed-size array. Before using the array
container the <array> header file must be included.
To define a std::array both the data type of its elements and its size
must be specified: the data type is given after an opening angle bracket,
immediately following the `array' container name. The array's size is
provided after the data type specification. Finally, a closing angle bracket
completes the array's type. Specifications like this are common practice with
containers. The combination of array, type and size defines a
type. As a result, array<string, 4> defines another type than
array<string, 5>, and a function explicitly defining an array<Type, N>
parameter will not accept an array<Type, M> argument if N and M
are unequal.
The array's size may may be defined as 0 (although such an array probably has
little use as it cannot store any element). The elements of an array are
stored contiguously. If array<Type, N> arr has been defined, then
&arr[n] + m == &arr[n + m], assuming than 0 <= n < N and 0 <= n + m
< N.
The following constructors, operators, and member functions are available:
array may be constructed with a fixed number N of
default elements:
array<string, N> object;
array<double, 4> dArr = {1.2, 2.4};
Here dArr is defined as an array of 4 element, with dArr[0] and
dArr[1] initialized to, respectively 1.2 and 2.4, and dArr[2] and
dArr[3] initialized to 0. An attractive characteristic of arrays (and
other containers) is that containers initialize
their data elements to the data type's default value. The data type's
default constructor is used for this initialization. With non-class
data types the value 0 is used. So, for an array<double, 4> array we know
that all but its explicitly initialized elements are initialized to
zero.
array
supports the index operator, which can be used to retrieve or reassign
individual elements of the array. Note that the elements which are indexed
must exist. For example, having defined an empty array a statement like
iarr[0] = 18 produces an error, as the array is empty. Note that
operator[] does not respect its
array bounds. If you want run-time array bound checking, use the array's
at member.
array class offers the following
member functions:
Type &at(size_t idx):idx. If idx exceeds the array's size a
std::out_of_range exception is thrown.
Type &back():array::iterator begin():end if the array is empty.
array::const_iterator cbegin():cend if the array is empty.
array::const_iterator cend():array::const_reverse_iterator crbegin():crend if the array is empty.
array::const_reverse_iterator crend():value_type *data():value_type const * is returned.
bool empty():true if the array contains no elements.
array::iterator end():void fill(Type const &item):item
Type &front():array::reverse_iterator rbegin():array::reverse_iterator rend():constexpr size_t size():void swap(array<Type, N> &other):swap.
array rather than a standard C style array offers several
advantages:
size can be used);
array container can be used in the context of templates,
there code is developed that operates on data types that become
available only after the code itself has been developed;
array supports reverse iterators, it can immediately be
used with generic algorithms performing `reversed' operations (e.g.,
to perform a descending rather than ascending sort (cf. section
19.1.54))
array or
vector (introduced in the next section) should be your `weapon of
choice'. Only if these containers demonstrably do not fit the problem at hand
you should use another type of container.
vector class implements an
expandable array. Before using the vector
container the <vector> header file must be included.
The following constructors, operators, and member functions are available:
vector may be constructed empty:
vector<string> object;
vector<string> object(5, "Hello"s); // initialize to 5 Hello's,
vector<string> container(10); // and to 10 empty strings
vector<string> names = {"george", "frank", "tony", "karel"};
Note the difference between vector<int> first(5) and vector<int>
second{ 5 }. The vector first contains five elements, initialized to 0,
while the vector second contains one element, initialized to 5. Referring
back to section 12.2: with the latter definition the compiler is able to
deduce
the vector's template parameter
type (int), so the latter definition could also have been written as
vector second{ 5 }.
An ambiguity might be observed when looking at
vector object{ vector{ 1 } };
Did we define a vector<int> or a vector<vector<int>>? The standard
considers this a vector<int>: it is initialized using the vector's move
constructor from an abstract vector<int>.
vector<string> the following construction may be used:
extern vector<string> container; vector<string> object(&container[5], &container[11]);
Note here that the last element pointed to by the second iterator
(&container[11]) is not stored in object. This is a simple
example of the use of iterators, in which the used
range of values starts at the first value, and includes all elements up
to but not including the element to which the second iterator refers. The
standard notation for this is [begin, end).
vector
supports the index operator, which can be used to retrieve or reassign
individual elements of the vector. Note that the elements which are indexed
must exist. For example, having defined an empty vector a statement like
ivect[0] = 18 produces an error, as the vector is empty. So, the vector
is not automatically
expanded, and operator[] does not respect its
array bounds. In this case the vector should be resized first, or
ivect.push_back(18) should be used (see below). If you need run-time array
bound checking, use the vector's at member.
vector class offers the following
member functions:
void assign(...):assign(iterator begin, iterator end) assigns the values at
the iterator range [begin, end) to the vector;
assign(size_type n, value_type const &val) assigns n
copies of val to the vector;
assign(initializer_list<value_type> values) assigns the
values in the initializer list to the vector.
Type &at(size_t idx):idx. If idx exceeds the vector's size a
std::out_of_range exception is thrown.
Type &back():vector::iterator begin():end if the vector is empty.
size_t capacity():size
vector::const_iterator cbegin():cend if the vector is empty.
vector::const_iterator cend():void clear():vector::const_reverse_iterator crbegin():crend if the vector is empty.
vector::const_reverse_iterator crend():value_type *data():iterator emplace(const_iterator position, Args &&...args):value_type object is constructed from the arguments
specified after position, and the newly created element is inserted at
position. Different from insert, which expects an existing object of
the container's value type (and inserts
the provided argument into the container) using copy or move construction or
assignment, emplace uses its arguments to
construct such an object immediately at the intended location of the
container, without requiring copy or move construction or assignment.
constexpr &emplace_back(Args &&...args):value_type object is constructed from the member's
arguments, and the newly created element is inserted beyond the vector's last
element, returning a reference to the newly added element.
bool empty():true if the vector contains no
elements.
vector::iterator end():vector::iterator erase():erase(pos) erases the element pointed to by the iterator
pos. The iterator ++pos is returned.
erase(first, beyond) erases elements indicated by the iterator
range [first, beyond), returning beyond.
Type &front():allocator_type get_allocator() const:vector object.
... insert():insert() that is called:
vector::iterator insert(pos) inserts a default value of type
Type at pos, pos is returned.
vector::iterator insert(pos, value) inserts value at
pos, pos is returned.
void insert(pos, first, beyond) inserts the elements in the
iterator range [first, beyond).
void insert(pos, n, value) inserts n elements having value
value at position pos.
size_t max_size():vector may contain.
void pop_back():size() member to return the (when cast to int) value -1, and
then -2, etc., etc.
void push_back(value):value to the end of the vector.
vector::reverse_iterator rbegin():vector::reverse_iterator rend():void reserve(size_t request):request is less than or equal to capacity, this
call has no effect. Otherwise, it is a request to allocate additional
memory. If the call is successful, then capacity returns a value of at
least request. Otherwise, capacity is unchanged. In either case,
size's return value won't change, until a function like resize is
called, actually changing the number of accessible elements.
void resize():resize(n, value) may be used to resize the vector to a size
of n. Value is optional. If the vector is expanded and value is
not provided, the additional elements are initialized to the default value
of the used data type, otherwise value is used to initialize extra
elements.
void shrink_to_fit():vector<Type>(vectorObject).swap(vectorObject)
idiom can be used.
size_t size():void swap(vector<Type> &other):
#include <iostream>
#include <vector>
using namespace std;
int main()
{
vector<int> v1(7);
vector<int> v2(10);
v1.swap(v2);
cout << v1.size() << " " << v2.size() << '\n';
}
/*
Produced output:
10 7
*/
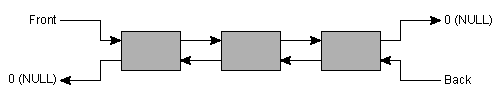
list container implements a list data structure.
Before using a list container the header file <list> must be included.
The organization of a list is shown in figure 10.

As a subtlety note that the representation given in figure 10 is not necessarily used in actual implementations of the list. For example, consider the following little program:
int main()
{
list<int> l;
cout << "size: " << l.size() << ", first element: " <<
l.front() << '\n';
}
When this program is run it might actually produce the output:
size: 0, first element: 0
Its front element can even be assigned a value. In this case the implementor has chosen to provide the list with a hidden element. The list actually is a circular list, where the hidden element serves as terminating element, replacing the 0-pointers in figure 10. As noted, this is a subtlety, which doesn't affect the conceptual notion of a list as a data structure ending in 0-pointers. Note also that it is well known that various implementations of list-structures are possible (cf. Aho, A.V., Hopcroft J.E. and Ullman, J.D., (1983) Data Structures and Algorithms (Addison-Wesley)).
Both lists and vectors are often appropriate data structures in situations where an unknown number of data elements must be stored. However, there are some rules of thumb to follow when selecting the appropriate data structure.
vector is the preferred data
structure. Example: in a program counting character frequencies in
a textfile, a vector<int> frequencies(256) is the
datastructure of choice, as the values of the received characters
can be used as indices into the frequencies vector.
vector: if the number of elements is known in
advance (and does not notably change during the lifetime of the
program), the vector is also preferred over the list.
vector should be the preferred container; even when
implementing algorithms traditionally using lists.
Other considerations related to the choice between lists and vectors should also be given some thought. Although it is true that the vector is able to grow dynamically, the dynamic growth requires data-copying. Clearly, copying a million large data structures takes a considerable amount of time, even on fast computers. On the other hand, inserting a large number of elements in a list doesn't require us to copy non-involved data. Inserting a new element in a list merely requires us to juggle some pointers. In figure 11 this is shown: a new element is inserted between the second and third element, creating a new list of four elements.
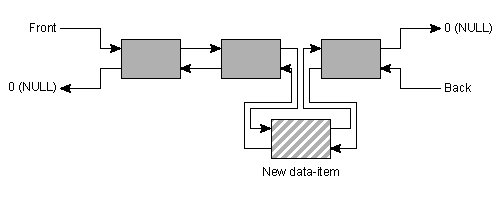
The list container offers the following constructors, operators, and
member functions:
list may be constructed empty:
list<string> object;
As with the vector, it is an error to refer to an element of an
empty list.
list<string> object(5, "Hello"s); // initialize to 5 Hello's list<string> container(10); // and to 10 empty strings
vector<string> the following construction may be used:
extern vector<string> container; list<string> object(&container[5], &container[11]);
list does not offer specialized operators, apart from the
standard operators for containers.
void assign(...):
assigns new content to the list:
assign(iterator begin, iterator end) assigns the values at
the iterator range [begin, end) to the list;
assign(size_type n, value_type const &val) assigns n
copies of val to the list;
Type &back():list::iterator begin():end if the list is
empty.
void clear():value_type &emplace_back(Args &&...args):value_type object is constructed from the member's
arguments, and the newly created element is inserted beyond the
last element of the list, returning a reference to the newly added
element.
value_type &emplace_front(Args &&...args):value_type object is constructed from the member's
arguments, and the newly created element is inserted before the
first element of the list, returning a reference to the newly added
element.
bool empty():true if the list contains no
elements.
list::iterator end():list::iterator erase():erase(pos) erases the element pointed to by pos. The
iterator ++pos is returned.
erase(first, beyond) erases elements indicated by the iterator
range [first, beyond). Beyond is returned.
Type &front():allocator_type get_allocator() const:list object.
... insert():insert that is called:
list::iterator insert(pos) inserts a default value of type
Type at pos, pos is returned.
list::iterator insert(pos, value) inserts value at
pos, pos is returned.
void insert(pos, first, beyond) inserts the elements in the
iterator range [first, beyond).
void insert(pos, n, value) inserts n elements having value
value at position pos.
size_t max_size():list may contain.
void merge(list<Type> other):sort). Based on that assumption, it inserts the
elements of other into the current list in such a way that the
modified list remains sorted. If both list are not sorted, the
resulting list will be ordered `as much as possible', given the
initial ordering of the elements in the two
lists. list<Type>::merge uses Type::operator< to sort the
data in the list, which operator must therefore be available. The
next example illustrates the use of the merge member: the list
`object' is not sorted, so the resulting list is ordered 'as
much as possible'.
#include <iostream>
#include <string>
#include <list>
using namespace std;
void showlist(list<string> &target)
{
for
(
list<string>::iterator from = target.begin();
from != target.end();
++from
)
cout << *from << " ";
cout << '\n';
}
int main()
{
list<string> first;
list<string> second;
first.push_back("alpha"s);
first.push_back("bravo"s);
first.push_back("golf"s);
first.push_back("quebec"s);
second.push_back("oscar"s);
second.push_back("mike"s);
second.push_back("november"s);
second.push_back("zulu"s);
first.merge(second);
showlist(first);
}
// shows:
// alpha bravo golf oscar mike november quebec zulu
A subtlety is that merge doesn't alter the list if the list
itself is used as argument: object.merge(object) won't change
the list `object'.
void pop_back():void pop_front():void push_back(value):value to the end of
the list.
void push_front(value):value before the
first element of the list.
list::reverse_iterator rbegin():void remove(value):value
from the list. In the following example, the two strings
`Hello' are removed from the list object:
#include <iostream>
#include <string>
#include <list>
using namespace std;
int main()
{
list<string> object;
object.push_back("Hello"s);
object.push_back("World"s);
object.push_back("Hello"s);
object.push_back("World"s);
object.remove("Hello"s);
while (object.size())
{
cout << object.front() << '\n';
object.pop_front();
}
}
/*
Generated output:
World
World
*/
void remove_if(Predicate pred):pred returns true. For each of the objects
stored in the list the predicate is called as pred(*iter),
where iter represents the iterator used internally by
remove_if. If a function pred is used, its prototype
should be bool pred(value_type const &object).
list::reverse_iterator rend():void resize():void reverse():back becomes front and vice
versa.
size_t size():void sort():unique member function
below. list<Type>::sort uses Type::operator< to sort the
data in the list, which must therefore be available.
void splice(pos, object):object to the current list, starting the insertion at the
iterator position pos of the object using the splice
member. Following splice, object is empty. For example:
#include <iostream>
#include <string>
#include <list>
using namespace std;
int main()
{
list<string> object;
object.push_front("Hello"s);
object.push_back("World"s);
list<string> argument(object);
object.splice(++object.begin(), argument);
cout << "Object contains " << object.size() << " elements, " <<
"Argument contains " << argument.size() <<
" elements,\n";
while (object.size())
{
cout << object.front() << '\n';
object.pop_front();
}
}
Alternatively, argument may be followed by an iterator of
argument, indicating the first element of argument that
should be spliced, or by two iterators begin and end
defining the iterator-range [begin, end) on argument
that should be spliced into object.
void swap():void unique():list<Type>::unique uses Type::operator== to identify
identical data elements, which operator must therefore be
available. Here's an example removing all multiply occurring
words from the list:
#include <iostream>
#include <string>
#include <list>
using namespace std;
// see the merge() example
void showlist(list<string> &target)
{
for
(
list<string>::iterator from = target.begin();
from != target.end();
++from
)
cout << *from << " ";
cout << '\n';
}
int main()
{
string
array[] =
{
"charlie",
"alpha",
"bravo",
"alpha"
};
list<string>
target
(
array, array + sizeof(array)
/ sizeof(string)
);
cout << "Initially we have:\n";
showlist(target);
target.sort();
cout << "After sort() we have:\n";
showlist(target);
target.unique();
cout << "After unique() we have:\n";
showlist(target);
}
/*
Generated output:
Initially we have:
charlie alpha bravo alpha
After sort() we have:
alpha alpha bravo charlie
After unique() we have:
alpha bravo charlie
*/
queue class implements a queue data structure. Before using a
queue container the header file <queue> must be included.
A queue is depicted in figure 13.
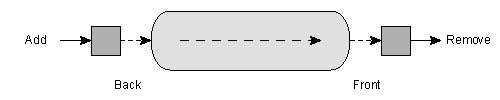
queue is therefore
also called a FIFO data structure, for first in, first out. It is
most often used in situations where events should be handled in the same order
as they are generated.
The following constructors, operators, and member functions are available
for the queue container:
queue may be constructed empty:
queue<string> object;
As with the vector, it is an error to refer to an element of an
empty queue.
queue container only supports the basic container operators.
Type &back():
value_type &emplace(Args &&...args):value_type object is constructed from the member's
arguments, and the newly created element is inserted beyond the
end of the queue, returning a reference to (or copy of) the newly
added element.
bool empty():true if the queue contains no elements.
Type &front():void pop():size() member to return the (when cast to int)
value -1, and then -2, etc., etc. One might wonder why
pop returns void, instead of a value of type Type
(cf. front). One reason is found in the principles of good software
design: functions should perform one task. Combining the removal and return of
the removed element breaks this principle. Moreover, when this principle is
abandoned pop's implementation is always flawed. Consider the
prototypical implementation of a pop member that is expected to return the
queue's front-value:
Type queue::pop()
{
Type ret{ front() };
erase_front();
return ret;
}
Since queue has no control over Type's behavior the first statement
(Type ret{ front() }) might throw. Although this still supports the
'commit or roll-back' principle, queue cannot guarantee that Type
offers copy-construction. Hence, pop does not return the queue's
front-value, but simply erases that element:
Type queue::pop()
{
erase_front();
}
Note that push doesn't require copy construction: push can also be
implemented when move-construction is supported. E.g.,
void queue::push(Type &&tmp)
{
d_data.push_back(std::move(tmp)); // uses move construction
}
Because of all this, we must first use front and then pop to
obtain and remove the queue's front element.
void push(value):value to the back of the queue.
size_t size():priority_queue class implements a priority queue data structure.
Before using a priority_queue container the <queue> header file must
have been included.
A priority queue is identical to a queue, but allows the entry of data
elements according to priority rules. A real-life priority queue is
found, e.g., at airport check-in terminals. At a terminal the passengers
normally stand in line to wait for their turn to check in, but late passengers
are usually allowed to jump the queue: they receive a higher priority than
other passengers.
The priority queue uses operator< of the data type stored in the
priority queue to decide about the priority of the data elements. The
smaller the value, the lower the priority. So, the priority queue
could be used to sort values while they arrive. A simple example of such
a priority queue application is the following program: it reads words from
cin and writes a sorted list of words to cout:
#include <iostream>
#include <string>
#include <queue>
using namespace std;
int main()
{
priority_queue<string> q;
string word;
while (cin >> word)
q.push(word);
while (q.size())
{
cout << q.top() << '\n';
q.pop();
}
}
Unfortunately, the words are listed in reversed order: because of the
underlying <-operator the words appearing later in the ASCII-sequence
appear first in the priority queue. A solution to that problem is to define a
wrapper class around the string datatype, reversing string's
operator<. Here is the modified program:
#include <iostream>
#include <string>
#include <queue>
class Text
{
std::string d_s;
public:
Text(std::string const &str)
:
d_s(str)
{}
operator std::string const &() const
{
return d_s;
}
bool operator<(Text const &right) const
{
return d_s > right.d_s;
}
};
using namespace std;
int main()
{
priority_queue<Text> q;
string word;
while (cin >> word)
q.push(word);
while (q.size())
{
word = q.top();
cout << word << '\n';
q.pop();
}
}
Other possibilities to achieve the same exist. One would be to store the content of the priority queue in, e.g., a vector, from which the elements can be read in reversed order.
The following constructors, operators, and member functions are available
for the priority_queue container:
priority_queue may be constructed empty:
priority_queue<string> object;
priority_queue only supports the basic operators of
containers.
bool empty():true if the
priority queue contains no elements.
void pop():queue avoid calling this member on an empty priority queue (cf. section
12.3.4.)
void push(value):value at the
appropriate position in the priority queue.
size_t size():Type &top():Note that the priority queue does not support iterators or an index operator. The only element that can be accessed is its top element. A priority queue can be emptied by:
deque (pronounce: `deck') class implements a
doubly ended queue data structure (deque). Before using a deque
container the header file <deque> must be included.
A deque is comparable to a queue, but it allows for reading and
writing at both ends. Actually, the deque data type supports a lot more
functionality than the queue, as illustrated by the following overview of
available member functions. A deque is a combination of a vector and
two queues, operating at both ends of the vector. In situations where random
insertions and the addition and/or removal of elements at one or both sides of
the vector occurs frequently using a deque should be considered.
The following constructors, operators, and member functions are available for deques:
deque may be constructed empty:
deque<string> object;
As with the vector, it is an error to refer to an element of an
empty deque.
deque<string> object(5, "Hello"s), // initialize to 5 Hello's deque<string> container(10); // and to 10 empty strings
vector<string> the following construction may be used:
extern vector<string> container; deque<string> object(&container[5], &container[11]);
void assign(...):
assigns new content to the deque:
assign(iterator begin, iterator end) assigns the values at
the iterator range [begin, end) to the deque;
assign(size_type n, value_type const &val) assigns n
copies of val to the deque;
Type &at(size_t idx):
returns a reference to the deque's element at index positionidx. Ifidxexceeds the deque's size astd::out_of_rangeexception is thrown.
Type &back():deque::iterator begin():deque::const_iterator cbegin():
returns a const_iterator pointing to the first
element in the deque, returning cend if the deque is empty.
deque::const_iterator cend():
returns a const_iterator pointing just beyond the deque's last element.
void clear():deque::const_reverse_iterator crbegin():
returns a const_reverse_iterator pointing to the last
element in the deque, returning crend if the deque is empty.
deque::const_reverse_iterator crend():
returns a const_reverse_iterator pointing just before the deque's first element.
iterator emplace(const_iterator position, Args &&...args)
avalue_typeobject is constructed from the arguments specified afterposition, and the newly created element is inserted atposition.
void emplace_back(Args &&...args)
a value_type object is constructed from the member's
arguments, and the newly created element is inserted beyond the deque's last
element.
void emplace_front(Args &&...args)
a value_type object is constructed from the member's
arguments, and the newly created element is inserted before the deque's first
element.
bool empty():true if the deque contains no elements.
deque::iterator end():deque::iterator erase():erase(pos) erases the element pointed to by pos. The
iterator ++pos is returned.
erase(first, beyond) erases elements indicated by the iterator
range [first, beyond). Beyond is returned.
Type &front():allocator_type get_allocator() const:deque object.
... insert():insert that is
called:
deque::iterator insert(pos) inserts a default value of type
Type at pos, pos is returned.
deque::iterator insert(pos, value) inserts value at
pos, pos is returned.
void insert(pos, first, beyond) inserts the elements in the
iterator range [first, beyond).
void insert(pos, n, value) inserts n elements having value
value starting at iterator position pos.
size_t max_size():deque may contain.
void pop_back():size() member to return the (when cast to
int) value -1, and then -2, etc., etc.
void pop_front():pop_back() its
internally maintained count of number of available elements is reduced
void push_back(value):value to the end of
the deque.
void push_front(value):value before the
first element of the deque.
deque::reverse_iterator rbegin():deque::reverse_iterator rend():void resize():resize(n, value) may be used to resize the deque to a size of
n. Value is optional. If the deque is expanded and value is not
provided, the additional elements are initialized to the default value of the
used data type, otherwise value is used to initialize extra elements.
void shrink_to_fit():deque<Type>(dequeObject).swap(dequeObject) idiom
can be used.
size_t size():void swap(argument):
map class offers a (sorted) associative array. Before using a
map container the <map> header file must be included.
A map is filled with key, value pairs, which may be of any
container-accepted type. Since types are associated with both the key and the
value, we must specify two types in the angle bracket notation, comparable
to the specification we've seen with the pair container (cf. section
12.2). The first type represents the key's type, the second type
represents the value's type. The key is used to access its associated
information. The map sorts the keys using their operator<, where the
smallest key values appears as first element in the map. For example, a
map in which the key is a string and the value is a double can be
defined as follows:
map<string, double> object;
That information is called the value. For example, a phone book uses the
names of people as the key, and uses the telephone number and maybe other
information (e.g., the zip-code, the address, the profession) as value. Since
a map sorts its keys, the key's operator< must be defined, and it
must be sensible to use it. For example, it is generally a bad idea to use
pointers for keys, as sorting pointers is something different than sorting the
values pointed at by those pointers. In addition to the key, value types,
a third type defines the comparison class, used to compare two keys. By
default, the comparison class is std::less<KeyType> (cf. section
18.1.2), using the key type's operator< to compare two key
values. For key type KeyType and value type ValueType the map's type
definition, therefore, looks like this:
map<KeyType, ValueType, std::less<KeyType>>
The two fundamental operations on maps are the storage of key, value
combinations, and the retrieval of values, given their keys. The index
operator using a key as the index, can be used for both. If the index operator
is used as lvalue, the expression's rvalue is inserted into the
map. If it is used as rvalue, the key's associated value is retrieved.
Each key can be stored only once in a map. If the same key is entered
again, the new value replaces the formerly stored value, which is lost.
A specific key, value combination can implicitly or explicitly be inserted
into a map. If explicit insertion is required, the key, value
combination must be constructed first. For this, every map defines a
value_type which may be used to create values that can be stored in the
map. For example, a value for a map<string, int> can be constructed as
follows:
map<string, int>::value_type siValue{ "Hello", 1 };
The value_type is associated with the map<string, int>: the
type of the key is string, the type of the value is int. Anonymous
value_type objects are also often used. E.g.,
map<string, int>::value_type{ "Hello", 1 };
Instead of using the line map<string, int>::value_type(...) over and
over again, a using declaration is frequently used to reduce typing and to
improve readability:
using StringIntValue = map<string, int>::value_type;
Now values for the map<string, int> may be specified this way:
StringIntValue{ "Hello", 1 };
Alternatively, pairs may be used to represent key, value
combinations used by maps:
pair<string, int>{ "Hello", 1 };
map container:
map may be constructed empty:
map<string, int> object;
Note that the values stored in maps may be containers themselves. For
example, the following defines a map in which the value is a pair: a
container
nested under another container:
map<string, pair<string, string>> object;
Note the use of the two consecutive closing angle brackets, which does not result in ambiguities as their syntactical context differs from their use as binary operators in expressions.
value_type values for the map to be constructed, or to
plain pair objects. If pairs are used, their first element represents
the type of the keys, and their second element represents the type of the
values. Example:
pair<string, int> pa[] =
{
pair<string,int>("one", 1),
pair<string,int>("two", 2),
pair<string,int>("three", 3),
};
map<string, int> object(&pa[0], &pa[3]);
In this example, map<string, int>::value_type could have been written
instead of pair<string, int> as well.
If begin represents the first iterator that is used to construct a map
and if end represents the second iterator, [begin, end) will be
used to initialize the map. Maybe contrary to intuition, the map
constructor only enters new keys. If the last element of pa would
have been "one", 3, only two elements would have entered the map:
"one", 1 and "two", 2. The value "one", 3 would silently have been
ignored.
The map receives its own copies of the data to which the iterators
point as illustrated by the following example:
#include <iostream>
#include <map>
using namespace std;
class MyClass
{
public:
MyClass()
{
cout << "MyClass constructor\n";
}
MyClass(MyClass const &other)
{
cout << "MyClass copy constructor\n";
}
~MyClass()
{
cout << "MyClass destructor\n";
}
};
int main()
{
pair<string, MyClass> pairs[] =
{
pair<string, MyClass>{ "one", MyClass{} }
};
cout << "pairs constructed\n";
map<string, MyClass> mapsm{ &pairs[0], &pairs[1] };
cout << "mapsm constructed\n";
}
/*
Generated output:
MyClass constructor
MyClass copy constructor
MyClass destructor
pairs constructed
MyClass copy constructor
mapsm constructed
MyClass destructor
MyClass destructor
*/
When tracing the output of this program, we see that, first, the
constructor of a MyClass object is called to initialize the anonymous
element of the array pairs. This object is then copied into the first
element of the array pairs by the copy constructor. Next, the original
element is not required anymore and is destroyed. At that point the array
pairs has been constructed. Thereupon, the map constructs a temporary
pair object, which is used to construct the map element. Having
constructed the map element, the temporary pair object is
destroyed. Eventually, when the program terminates, the pair element
stored in the map is destroyed too.
The index operator may be used to retrieve or reassign individual elements of the map. The argument of the index operator is called a key.
If the provided key is not available in the map, a new data element is
automatically added to the map using the default value or default
constructor to initialize the value part of the new element. This default
value is returned if the index operator is used as an rvalue.
When initializing a new or reassigning another element of the map, the type of
the right-hand side of the assignment operator must be equal to (or promotable
to) the type of the map's value part. E.g., to add or change the value of
element "two" in a map, the following statement can be used:
mapsm["two"] = MyClass{};
map container:
mapped_type &at(key_type const &key):mapped_type
associated with key. If the key is not stored in the map an
std::out_of_range exception is thrown.
map::iterator begin():map::const_iterator cbegin():cend if the map is empty.
map::const_iterator cend():void clear():size_t count(key):map, otherwise 0 is returned.
map::reverse_iterator crbegin() const:map::reverse_iterator crend():pair<iterator, bool> emplace(Args &&...args):value_type object is constructed from emplace's
arguments. If the map already contained an object using the same
key_type value, then a std::pair is returned containing an iterator
pointing to the object using the same key_type value and the value
false. If no such key_type value was found, the newly constructed
object is inserted into the map, and the returned std::pair
contains an iterator pointing to the newly inserted value_type
as well as the value true.
iterator emplace_hint(const_iterator position,
Args &&...args):value_type object is constructed from the member's
arguments, and the newly created element is inserted into the
map, unless the (at args) provided key already exists. The
implementation may or may not use position as a hint to start looking
for an insertion point. The returned iterator points to the value_type
using the provided key. It may refer to an already existing value_type or
to a newly added value_type; an existing value_type is not
replaced. If a new value was added, then the container's size has been
incremented when emplace_hint returns.
bool empty():true if
the map contains no elements.
map::iterator end():pair<map::iterator, map::iterator> equal_range(key):lower_bound and upper_bound, introduced below.
An example illustrating these member functions is given at the
discussion of the member function upper_bound.
... erase():bool erase(key) erases the element having the
given key from the map. True is returned if the value was removed,
false if the map did not contain an element using the given key.
void erase(pos) erases the element pointed to by the iterator
pos.
void erase(first, beyond) erases all elements indicated by
the iterator range [first, beyond).
map::iterator find(key):end is returned. The following example illustrates the use of
the find member function:
#include <iostream>
#include <map>
using namespace std;
int main()
{
map<string, int> object;
object["one"] = 1;
map<string, int>::iterator it = object.find("one");
cout << "`one' " <<
(it == object.end() ? "not " : "") << "found\n";
it = object.find("three");
cout << "`three' " <<
(it == object.end() ? "not " : "") << "found\n";
}
/*
Generated output:
`one' found
`three' not found
*/
allocator_type get_allocator() const:map object.
... insert():insert that is called:
pair<map::iterator, bool> insert(keyvalue) inserts
a new value_type into the map. The return value is a
pair<map::iterator, bool>. If the returned bool field is true,
keyvalue was inserted into the map. The value false indicates that the
key that was specified in keyvalue was already available in the map, and
so keyvalue was not inserted into the map. In both cases the
map::iterator field points to the data element having the
key that was specified in keyvalue. The use of this variant of
insert is illustrated by the following example:
#include <iostream>
#include <string>
#include <map>
using namespace std;
int main()
{
pair<string, int> pa[] =
{
pair<string,int>("one", 10),
pair<string,int>("two", 20),
pair<string,int>("three", 30),
};
map<string, int> object(&pa[0], &pa[3]);
// {four, 40} and `true' is returned
pair<map<string, int>::iterator, bool>
ret = object.insert
(
map<string, int>::value_type
("four", 40)
);
cout << boolalpha;
cout << ret.first->first << " " <<
ret.first->second << " " <<
ret.second << " " << object["four"] << '\n';
// {four, 40} and `false' is returned
ret = object.insert
(
map<string, int>::value_type
("four", 0)
);
cout << ret.first->first << " " <<
ret.first->second << " " <<
ret.second << " " << object["four"] << '\n';
}
/*
Generated output:
four 40 true 40
four 40 false 40
*/
Note the somewhat peculiar constructions like
cout << ret.first->first << " " << ret.first->second << ...
Note that `ret' is equal to the pair returned by the
insert member function. Its `first' field is an iterator into the
map<string, int>, so it can be considered a pointer to a map<string,
int>::value_type. These value types themselves are pairs too, having
`first' and `second' fields. Consequently, `ret.first->first' is
the key of the map value (a string), and `ret.first->second' is
the value (an int).
map::iterator insert(pos, keyvalue). This way a
map::value_type may also be inserted into the map. pos is ignored, and
an iterator to the inserted element is returned.
void insert(first, beyond) inserts the (map::value_type)
elements pointed to by the iterator range [first, beyond). Values that
were already present are not replaced.
key_compare key_comp():map to compare keys. The
type map<KeyType, ValueType>::key_compare is defined by the map
container and key_compare's parameters have types KeyType const
&. The comparison function returns true if the first key
argument should be ordered before the second key argument. To compare
keys and values, use value_comp, listed below.
map::iterator lower_bound(key):keyvalue element of which the key is at least equal to the specified
key. If no such element exists, the function returns end.
size_t max_size():map may contain.
map::reverse_iterator rbegin():map::reverse_iterator rend():size_t size():void swap(argument):map::iterator upper_bound(key):keyvalue element having a key exceeding the specified key. If no
such element exists, the function returns end. The following
example illustrates the member functions equal_range, lower_bound
and upper_bound:
#include <iostream>
#include <map>
using namespace std;
int main()
{
pair<string, int> pa[] =
{
pair<string,int>("one", 10),
pair<string,int>("two", 20),
pair<string,int>("three", 30),
};
map<string, int> object(&pa[0], &pa[3]);
map<string, int>::iterator it;
if ((it = object.lower_bound("tw")) != object.end())
cout << "lower-bound `tw' is available, it is: " <<
it->first << '\n';
if (object.lower_bound("twoo") == object.end())
cout << "lower-bound `twoo' not available" << '\n';
cout << "lower-bound two: " <<
object.lower_bound("two")->first <<
" is available\n";
if ((it = object.upper_bound("tw")) != object.end())
cout << "upper-bound `tw' is available, it is: " <<
it->first << '\n';
if (object.upper_bound("twoo") == object.end())
cout << "upper-bound `twoo' not available" << '\n';
if (object.upper_bound("two") == object.end())
cout << "upper-bound `two' not available" << '\n';
pair
<
map<string, int>::iterator,
map<string, int>::iterator
>
p = object.equal_range("two");
cout << "equal range: `first' points to " <<
p.first->first << ", `second' is " <<
(
p.second == object.end() ?
"not available"
:
p.second->first
) <<
'\n';
}
/*
Generated output:
lower-bound `tw' is available, it is: two
lower-bound `twoo' not available
lower-bound two: two is available
upper-bound `tw' is available, it is: two
upper-bound `twoo' not available
upper-bound `two' not available
equal range: `first' points to two, `second' is not available
*/
value_compare value_comp():map to compare keys. The
type map<KeyType, ValueType>::value_compare is defined by the map
container and value_compare's parameters have types value_type
const &. The comparison function returns true if the first
key argument should be ordered before the second key argument. The
Value_Type elements of the value_type objects passed to this
member are not used by the returned function.
map represents
a sorted associative array. In a map the keys are sorted. If an
application must visit all elements in a map the begin and end
iterators must be used.
The following example illustrates how to make a simple table listing all keys and values found in a map:
#include <iostream>
#include <iomanip>
#include <map>
using namespace std;
int main()
{
pair<string, int>
pa[] =
{
pair<string,int>("one", 10),
pair<string,int>("two", 20),
pair<string,int>("three", 30),
};
map<string, int>
object(&pa[0], &pa[3]);
for
(
map<string, int>::iterator it = object.begin();
it != object.end();
++it
)
cout << setw(5) << it->first.c_str() <<
setw(5) << it->second << '\n';
}
/*
Generated output:
one 10
three 30
two 20
*/
map, the multimap class implements a (sorted)
associative array. Before using a multimap container the header
file <map> must be included.
The main difference between the map and the multimap is that the
multimap supports multiple values associated with the same key, whereas the
map contains single-valued keys. Note that the multimap also accepts multiple
identical values associated with identical keys.
The map and the multimap have the same set of constructors and member
functions, with the exception of the index operator which is not supported
with the multimap. This is understandable: if
multiple entries of the same key are allowed, which of the possible values
should be returned for object[key]?
Refer to section 12.3.7 for an overview of
the multimap member functions. Some member functions, however, deserve
additional attention when used in the context of the multimap
container. These members are discussed below.
size_t map::count(key):key.
... erase():size_t erase(key) erases all elements having the
given key. The number of erased elements is returned.
void erase(pos) erases the single element pointed to by
pos. Other elements possibly having the same keys are not erased.
void erase(first, beyond) erases all elements indicated by
the iterator range [first, beyond).
pair<multimap::iterator, multimap::iterator> equal_range(key):lower_bound and upper_bound, introduced below. The function provides
a simple means to determine all elements in the multimap that have the
same keys. An example illustrating the use of these member functions is
given at the end of this section.
multimap::iterator find(key):key. If the element isn't available, end is returned. The
iterator could be incremented to visit all elements having the same key
until it is either end, or the iterator's first member is
not equal to key anymore.
multimap::iterator insert():pair<multimap::iterator, bool> as returned with the
map container. The returned iterator points to the newly added element.
lower_bound and upper_bound act
identically in the map and multimap containers, their operation in a
multimap deserves some additional attention. The next example illustrates
lower_bound, upper_bound and
equal_range applied to a multimap:
#include <iostream>
#include <map>
using namespace std;
int main()
{
pair<string, int> pa[] =
{
pair<string,int>("alpha", 1),
pair<string,int>("bravo", 2),
pair<string,int>("charlie", 3),
pair<string,int>("bravo", 6), // unordered `bravo' values
pair<string,int>("delta", 5),
pair<string,int>("bravo", 4),
};
multimap<string, int> object(&pa[0], &pa[6]);
using msiIterator = multimap<string, int>::iterator;
msiIterator it = object.lower_bound("brava");
cout << "Lower bound for `brava': " <<
it->first << ", " << it->second << '\n';
it = object.upper_bound("bravu");
cout << "Upper bound for `bravu': " <<
it->first << ", " << it->second << '\n';
pair<msiIterator, msiIterator>
itPair = object.equal_range("bravo");
cout << "Equal range for `bravo':\n";
for (it = itPair.first; it != itPair.second; ++it)
cout << it->first << ", " << it->second << '\n';
cout << "Upper bound: " << it->first << ", " << it->second << '\n';
cout << "Equal range for `brav':\n";
itPair = object.equal_range("brav");
for (it = itPair.first; it != itPair.second; ++it)
cout << it->first << ", " << it->second << '\n';
cout << "Upper bound: " << it->first << ", " << it->second << '\n';
}
/*
Generated output:
Lower bound for `brava': bravo, 2
Upper bound for `bravu': charlie, 3
Equal range for `bravo':
bravo, 2
bravo, 6
bravo, 4
Upper bound: charlie, 3
Equal range for `brav':
Upper bound: bravo, 2
*/
In particular note the following characteristics:
lower_bound and upper_bound produce the same result for
non-existing keys: they both return the first element having a key that
exceeds the provided key.
multimap, the values for
equal keys are not ordered: they are retrieved in the order in which they were
entered.
set class implements a sorted collection of values. Before using
set containers the <set> header file must be included.
A set contains unique values (of a container-acceptable type). Each value
is stored only once, and the set sorts its values using their
operator<, where the smallest values appears as first element in the set.
A specific value can be explicitly created: Every set defines a
value_type which may be used to create values that can be stored in the
set. For example, a value for a set<string> can be constructed as
follows:
set<string>::value_type setValue{ "Hello" };
Like the std::map container, the std::set also has an additional
parameter declaring the class that is used for comparing values in the set.
For value type ValueType the set's type definition, therefore, looks like
this:
set<ValueType, std::less<ValueType>>
The value_type is associated with the set<string>. Anonymous
value_type objects are also often used. E.g.,
set<string>::value_type{ "Hello" };
Instead of using the line set<string>::value_type(...) over
and over again, a using declaration is often used to reduce typing and to
improve readability:
using StringSetValue = set<string>::value_type;
Now values for the set<string> may be constructed as follows:
StringSetValue{ "Hello" };
Alternatively, values of the set's type may be used
immediately. In that case the value of type Type is implicitly
converted to a set<Type>::value_type.
The following constructors, operators, and member functions are available
for the set container:
set may be constructed empty:
set<int> object;
int intarr[] = {1, 2, 3, 4, 5};
set<int> object{ &intarr[0], &intarr[5] };
Note that all values in the set must be different: it is not possible to store the same value repeatedly when the set is constructed. If the same value occurs repeatedly, only the first instance of the value is entered into the set; the remaining values are silently ignored.
Like the map, the set receives its own copy of the data it
contains.
set container only supports the standard set of operators
that are available for containers.
set class has the following member functions:
set::iterator begin():end is returned.
void clear():size_t count(value):set, otherwise 0 is returned.
pair<iterator, bool> emplace(Args &&...args):value_type object is constructed from the member's
arguments, and the newly created element is inserted into the
set. The return value's second member is true if the
element is inserted, and false if the element was already
available. The pair's first element is an iterator referring
to the set's eement.
bool empty():true if
the set contains no elements.
set::iterator end():pair<set::iterator, set::iterator> equal_range(value):lower_bound and upper_bound, introduced
below.
... erase():bool erase(value) erases the element having the given
value from the set. True is returned if the value was removed,
false if the set did not contain an element `value'.
void erase(pos) erases the element pointed to by the iterator
pos.
void erase(first, beyond) erases all elements
indicated by the iterator range [first, beyond).
set::iterator find(value):end is returned.
allocator_type get_allocator() const:set object.
... insert():set. If the
element already exists, the existing element is left untouched and the element
to be inserted is ignored. The return value depends on the version of
insert that is called:
pair<set::iterator, bool> insert(value) inserts
a new set::value_type into the set. The return value is a
pair<set::iterator, bool>. If the returned bool field is true,
value was inserted into the set. The value false indicates that the
value that was specified was already available in the set, and
so the provided value was not inserted into the set. In both cases the
set::iterator field points to the data element in the set having the
specified value.
set::iterator insert(pos, value). This way a
set::value_type may also be inserted into the set. pos is ignored, and
an iterator to the inserted element is returned.
void insert(first, beyond) inserts the (set::value_type)
elements pointed to by the iterator range [first, beyond) into the
set. Values that were already present are not replaced.
key_compare key_comp():set to compare keys. The
type set<ValueType>::key_compare is defined by the set container
and key_compare's parameters have types ValueType const &. The
comparison function returns true if its first argument should
be ordered before its second argument.
set::iterator lower_bound(value):value element of
which the value is at least equal to the specified value. If no
such element exists, the function returns end.
size_t max_size():set may contain.
set::reverse_iterator rbegin():set::reverse_iterator rend:size_t size():void swap(argument):argument being
the second set) that use identical data types.
set::iterator upper_bound(value):value element having a value exceeding the specified value. If no
such element exists, the function returns end.
value_compare value_comp():set to compare values. The
type set<ValueType>::value_compare is defined by the set container and
value_compare's parameters have types ValueType const &. The
comparison function returns true if its first argument should be
ordered before its second argument. Its operation is identical to that
of a key_compare object, returned by key_comp.
set, the multiset class implements a
sorted collection of values. Before
using multiset containers the header file <set> must be included.
The main difference between the set and the multiset is that the
multiset supports multiple entries of the same value, whereas the set
contains unique values.
The set and the multiset have the same set of constructors and member
functions. Refer to section 12.3.9 for an overview of the member functions
that can be used with the multiset. Some member functions, however,
behave slightly different than their counterparts of the set
container. Those members are:
size_t count(value):value.
... erase():size_t erase(value) erases all elements having the given
value. The number of erased elements is returned.
void erase(pos) erases the element pointed to by the iterator
pos. Other elements possibly having the same values are not erased.
void erase(first, beyond) erases all elements indicated by
the iterator range [first, beyond).
pair<multiset::iterator, multiset::iterator> equal_range(value):lower_bound and upper_bound, introduced below. The function provides
a simple means to determine all elements in the multiset that have the
same values.
multiset::iterator find(value):end is returned. The iterator could be
incremented to visit all elements having the given value until it is
either end, or the iterator doesn't point to `value' anymore.
... insert():pair<multiset::iterator,
bool> as returned with the set container. The returned iterator points to
the newly added element.
lower_bound and upper_bound act identically
in the set and multiset containers, their operation in a multiset
deserves some additional attention. With a multiset container
lower_bound and upper_bound produce the same result for non-existing
keys: they both return the first element having a key exceeding the provided
key.
Here is an example showing the use of various member functions of a multiset:
#include <iostream>
#include <set>
using namespace std;
int main()
{
string
sa[] =
{
"alpha",
"echo",
"hotel",
"mike",
"romeo"
};
multiset<string>
object(&sa[0], &sa[5]);
object.insert("echo");
object.insert("echo");
multiset<string>::iterator
it = object.find("echo");
for (; it != object.end(); ++it)
cout << *it << " ";
cout << '\n';
cout << "Multiset::equal_range(\"ech\")\n";
pair
<
multiset<string>::iterator,
multiset<string>::iterator
>
itpair = object.equal_range("ech");
if (itpair.first != object.end())
cout << "lower_bound() points at " << *itpair.first << '\n';
for (; itpair.first != itpair.second; ++itpair.first)
cout << *itpair.first << " ";
cout << '\n' <<
object.count("ech") << " occurrences of 'ech'" << '\n';
cout << "Multiset::equal_range(\"echo\")\n";
itpair = object.equal_range("echo");
for (; itpair.first != itpair.second; ++itpair.first)
cout << *itpair.first << " ";
cout << '\n' <<
object.count("echo") << " occurrences of 'echo'" << '\n';
cout << "Multiset::equal_range(\"echoo\")\n";
itpair = object.equal_range("echoo");
for (; itpair.first != itpair.second; ++itpair.first)
cout << *itpair.first << " ";
cout << '\n' <<
object.count("echoo") << " occurrences of 'echoo'" << '\n';
}
/*
Generated output:
echo echo echo hotel mike romeo
Multiset::equal_range("ech")
lower_bound() points at echo
0 occurrences of 'ech'
Multiset::equal_range("echo")
echo echo echo
3 occurrences of 'echo'
Multiset::equal_range("echoo")
0 occurrences of 'echoo'
*/
stack class implements a stack data structure. Before using
stack containers the header file <stack> must be included.
A stack is also called a first in, last out (FILO or LIFO) data structure as the first item to enter the stack is the last item to leave. A stack is an extremely useful data structure in situations where data must temporarily remain available. For example, programs maintain a stack to store local variables of functions: the lifetime of these variables is determined by the time these functions are active, contrary to global (or static local) variables, which live for as long as the program itself lives. Another example is found in calculators using the Reverse Polish Notation (RPN), in which the operands of operators are kept in a stack, whereas operators pop their operands off the stack and push the results of their work back onto the stack.
As an example of the use of a stack, consider figure 14, in which
the content of the stack is shown while the expression (3 + 4) * 2 is
evaluated. In the RPN this expression becomes 3 4 + 2 *, and figure
14 shows the stack content after each token (i.e., the
operands and the operators) is read from the input. Notice that each operand
is indeed pushed on the stack, while each operator changes the content of the
stack.
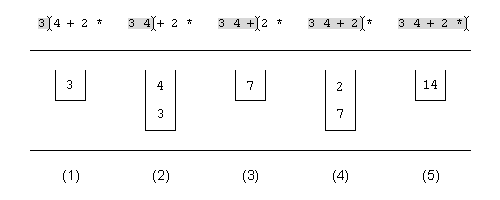
3 4 + 2 *
3) is now at
the bottom of the stack. Next, in step 3, the + operator is read. The
operator pops two operands (so that the stack is empty at that moment),
calculates their sum, and pushes the resulting value (7) on the
stack. Then, in step 4, the number 2 is read, which is dutifully pushed on
the stack again. Finally, in step 5 the final operator * is read, which
pops the values 2 and 7 from the stack, computes their product, and
pushes the result back on the stack. This result (14) could then be popped
to be displayed on some medium.
From figure 14 we see that a stack has one location (the top) where items can be pushed onto and popped off the stack. This top element is the stack's only immediately visible element. It may be accessed and modified directly.
Bearing this model of the stack in mind, let's see what we formally can do
with the stack container. For the stack, the following constructors,
operators, and member functions are available:
stack may be constructed empty:
stack<string> object;
stack
value_type &emplace(Args &&...args):value_type object is constructed from the member's
arguments, and the newly created element is pushed on the stack.
The return value is a reference to (or copy of) the newly pushed
value.
bool empty():true if the stack contains no elements.
void pop():pop has
return type void and why pop should not be called on an empty
stack.
void push(value):value at the top of the stack, hiding the other elements from view.
size_t size():Type &top():The stack does not support iterators or an index operator. The only elements that can be accessed is its top element. To empty a stack:
unordered_map.
Before using unordered_map or unordered_multimap containers the header
file <unordered_map> must be included.
The unordered_map class implements an associative array in which the
elements are stored according to some hashing scheme. As discussed, the
map is a sorted data structure. The keys in maps are sorted using the
operator< of the key's data type. Generally, this is not the fastest way
to either store or retrieve data. The main benefit of sorting is that a
listing of sorted keys appeals more to humans than an unsorted list. However,
a by far faster way to store and retrieve data is to use hashing.
Hashing uses a function (called the hash function) to compute an (unsigned) number from the key, which number is thereupon used as an index in the table storing the keys and their values. This number is called the bucket number. Retrieval of a key is as simple as computing the hash value of the provided key, and looking in the table at the computed index location: if the key is present, it is stored in the table, at the computed bucket location and its value can be returned. If it's not present, the key is not currently stored in the container.
Collisions occur when a computed index position is already
occupied by another element. For these situations the abstract containers have
solutions available. A simple solution, used by unordered_maps, consists
of using linear chaining, which uses linked list to store colliding table
elements.
The term unordered_map is used rather than hash to avoid name collisions with hash tables developed before they were added to the language.
Because of the hashing method, the efficiency of a unordered_map in
terms of speed should greatly exceed the efficiency of the map. Comparable
conclusions may be drawn for the unordered_set, the unordered_multimap
and the unordered_multiset.
unordered_map type five template arguments must be
specified :
unordered_map::key_type),
unordered_map::mapped_type),
unordered_map::hasher), and
unordered_map::key_equal).
The generic definition of an unordered_map container looks like this:
std::unordered_map <KeyType, ValueType, hash type, predicate type,
allocator type>
When KeyType is std::string or a built-in type then default types
are available for the hash type and the predicate type. In practice the
allocator type is not specified, as the default allocator suffices. In these
cases an unordered_map object can be defined by merely specifying the key-
and value types, like this:
std::unordered_map<std::string, ValueType> hash(size_t size = implSize);
Here, implSize is the container's default initial size, which is
specified by the implementor. The map's size is automatically enlarged by the
unordered_map when necessary, in which case the container rehashes all
its elements. In practice the default size argument provided by the
implementor is completely satisfactory.
The KeyType frequently consists of text. So, a unordered_map using a
std::string KeyType is frequently used. Be careful not to use a plain
char const * key_type as two char const * values pointing to equal
C-strings stored at different locations are considered to be different
keys, as their pointer values rather than their textual content are
compared. Here is an example showing how a char const * KeyType can be
used. Note that in the example no arguments are specified when constructing
months, since default values and constructors are available:
#include <unordered_map>
#include <iostream>
#include <string>
#include <cstring>
using namespace std;
struct EqualCp
{
bool operator()(char const *l, char const *r) const
{
return strcmp(l, r) == 0;
}
};
struct HashCp
{
size_t operator()(char const *str) const
{
return std::hash<std::string>()(str);
}
};
int main()
{
unordered_map<char const *, int, HashCp, EqualCp> months;
// or explicitly:
unordered_map<char const *, int, HashCp, EqualCp>
monthsTwo(61, HashCp(), EqualCp());
months["april"] = 30;
months["november"] = 31;
string apr("april"); // different pointers, same string
cout << "april -> " << months["april"] << '\n' <<
"april -> " << months[apr.c_str()] << '\n';
}
If other KeyTypes must be used, then the unordered_map's constructor
requires (constant references to) a hash function object, computing a hash
value from a key value, and a predicate function object, returning true if
two unordered_map::key_type objects are identical. A generic
algorithm (see chapter 19) exists performing tests of equality
(i.e., equal_to). These tests can be used if the key's data type supports
the equality operator. Alternatively, an overloaded operator== or
specialized function object could be constructed returning true if two
keys are equal and false otherwise.
Constructors
The unordered_map supports the following constructors:
explicit unordered_map(size_type n = implSize,
hasher const &hf = hasher(),key_equal const &eql = key_equal(),allocator_type const &alloc = allocator_type()):
this constructor can also be used as default constructor;
unordered_map(const_iterator begin,
const_iterator end,
size_type n = implSize, hasher const &hf = hasher(),
key_equal const &eql = key_equal(),
allocator_type const &alloc = allocator_type()):
this constructor expects two iterators specifying
a range of unordered_map::value_type const objects, and
unordered_map(initializer_list<value_type> initList,
size_type n = implSize, hasher const &hf = hasher(),
key_equal const &eql = key_equal(),
allocator_type const &alloc = allocator_type()):
a constructor expecting an initializer_list of
unordered_map::value_type values.
The following example shows a program using an unordered_map containing
the names of the months of the year and the number of days these months
(usually) have. Then, using the subscript operator the days in several months
are displayed (the predicate used here is the generic algorithm
equal_to<string>, which is provided by the compiler as the default fourth
argument of the unordered_map constructor):
#include <unordered_map>
#include <iostream>
#include <string>
using namespace std;
int main()
{
unordered_map<string, int> months;
months["january"] = 31;
months["february"] = 28;
months["march"] = 31;
months["april"] = 30;
months["may"] = 31;
months["june"] = 30;
months["july"] = 31;
months["august"] = 31;
months["september"] = 30;
months["october"] = 31;
months["november"] = 30;
months["december"] = 31;
cout << "september -> " << months["september"] << '\n' <<
"april -> " << months["april"] << '\n' <<
"june -> " << months["june"] << '\n' <<
"november -> " << months["november"] << '\n';
}
/*
Generated output:
september -> 30
april -> 30
june -> 30
november -> 30
*/
unordered_map supports the index operator operating identically to the
map's index operator: a (const) reference to the ValueType associated
with the provided KeyType's value is returned. If not yet available, the
key is added to the unordered_map, and a default ValueType value is
returned. In addition, it supports operator==.
The unordered_map provides the following
member functions (key_type,
value_type etc. refer to the types defined by the unordered_map):
mapped_type &at(key_type const &key):mapped_type
associated with key. If the key is not stored in the unordered_map a
std::out_of_range exception is thrown.
unordered_map::iterator begin():end if the unordered_map is empty.
size_t bucket(key_type const &key):key is stored. If
key wasn't stored yet bucket adds value_type(key, Value()) before
returning its index position.
size_t bucket_count():value_type objects.
size_t bucket_size(size_t index):value_type objects stored at bucket
position index.
unordered_map::const_iterator cbegin():cend if the unordered_map is empty.
unordered_map::const_iterator cend():void clear():size_t count(key_type const &key):value_type object using
key_type key is stored in the unordered_map (which is either one
or zero).
pair<iterator, bool> emplace(Args &&...args):value_type object is constructed from emplace's
arguments. If the unordered_map already contained an object using the same
key_type value, then a std::pair is returned containing an iterator
pointing to the object using the same key_type value and the value
false. If no such key_type value was found, the newly constructed
object is inserted into the unordered_map, and the returned std::pair
contains an iterator pointing to the newly inserted inserted value_type
as well as the value true.
iterator emplace_hint(const_iterator position,
Args &&...args):value_type object is constructed from the member's
arguments, and the newly created element is inserted into the
unordered_map, unless the (at args) provided key already exists. The
implementation may or may not use position as a hint to start looking
for an insertion point. The returned iterator points to the value_type
using the provided key. It may refer to an already existing value_type or
to a newly added value_type; an existing value_type is not
replaced. If a new value was added, then the container's size has been
incremented when emplace_hint returns.
bool empty():true if the unordered_map contains no elements.
unordered_map::iterator end():pair<iterator, iterator> equal_range(key):key. With the unordered_map this range includes
at most one element.
unordered_map::iterator erase():bool erase(key) erases the element having the
given key from the map. True is returned if the value was removed,
false if the map did not contain an element using the given key.
erase(pos) erases the element pointed to by the iterator
pos. The iterator ++pos is returned.
erase(first, beyond) erases elements indicated by the iterator
range [first, beyond), returning beyond.
iterator find(key):end is returned.
allocator_type get_allocator() const:unordered_map object.
hasher hash_function() const:unordered_map object.
... insert():
elements may be inserted starting at a certain position. No insertion is performed if the provided key is already in use. The return value depends on the version ofinsert()that is called. When apair<iterator, bool>is returned, then thepair's firstmember is an iterator pointing to the element having a key that is equal to the key of the providedvalue_type, thepair's secondmember istrueifvaluewas actually inserted into the container, andfalseif not.
pair<iterator, bool> insert(value_type const &value)
attempts to insert value.
pair<iterator, bool> insert(value_type &&tmp)
attempts to insert value using value_type's move
constructor.
pair<iterator, bool> insert(const_iterator hint, value_type
const &value)
attempts to insert value, possibly using hint as a
starting point when trying to insert value.
pair<iterator, bool> insert(const_iterator hint, value_type
&&tmp)
attempts to insert a value using value_type's move
constructor, and possibly using hint as a starting point when trying to
insert value.
void insert(first, beyond) tries to insert the elements in
the iterator range [first, beyond).
void insert(initializer_list <value_type> iniList)
attempts to insert the elements in iniList into the
container.
hasher key_eq() const:key_equal function object used by the unordered_map object.
float load_factor() const:size / bucket_count.
size_t max_bucket_count():unordered_map may contain.
float max_load_factor() const:load_factor.
void max_load_factor(float max):max. When a load factor of max is
reached, the container will enlarge its bucket_count, followed by a rehash
of its elements. Note that the container's default maximum load factor equals
1.0
size_t max_size():unordered_map may contain.
void rehash(size_t size):size exceeds the current bucket count, then the bucket
count is increased to size, followed by a rehash of its elements.
void reserve(size_t request):request is less than or equal to the current bucket count,
this call has no effect. Otherwise, the bucket count is increased to a value
of at least request, followed by a rehash of the container's elements.
size_t size():void swap(unordered_map &other):unordered_map.
unordered_multimap allows multiple objects using the same keys to be
stored in an unordered map. The unordered_multimap container offers the
same set of members and constructors as the unordered_map, but without the
unique-key restriction imposed upon the unordered_map.
The unordered_multimap does not offer operator[] and does not offer
at members.
Below all members are described whose behavior differs from the behavior of
the corresponding unordered_map members:
at
not supported by the unordered_multimap container
size_t count(key_type const &key):value_type object using
key_type key is stored in the unordered_map. This member is
commonly used to verify whether key is available in the
unordered_multimap.
iterator emplace(Args &&...args):value_type object is constructed from emplace's
arguments. The returned iterator points to the newly inserted inserted
value_type.
iterator emplace_hint(const_iterator position,
Args &&...args):value_type object is constructed from the member's
arguments, and the newly created element is inserted into the
unordered_multimap. The
implementation may or may not use position as a hint to start looking
for an insertion point. The returned iterator points to the value_type
using the provided key.
pair<iterator, iterator> equal_range(key):key.
iterator find(key):end is returned.
... insert():
elements may be inserted starting at a certain position. The return value depends on the version ofinsert()that is called. When aniteratoris returned, then it points to the element that was inserted.
iterator insert(value_type const &value)
inserts value.
iterator insert(value_type &&tmp)
inserts value using value_type's move
constructor.
iterator insert(const_iterator hint, value_type const &value)
inserts value, possibly using hint as a
starting point when trying to insert value.
iterator insert(const_iterator hint, value_type &&tmp)
inserts value using value_type's move
constructor, and possibly using hint as a starting point when trying to
insert value.
void insert(first, beyond) inserts the elements in
the iterator range [first, beyond).
void insert(initializer_list <value_type> iniList)
inserts the elements in iniList into the container.
map container, orders its elements. If
ordering is not an issue, but fast lookups are, then a hash-based set and/or
multi-set may be preferred. C++ provides such hash-based sets and
multi-sets: the unordered_set and unordered_multiset.
Before using these hash-based set containers the header file
<unordered_set> must be included.
Elements stored in the unordered_set are immutable, but they can be
inserted and removed from the container. Different from the unordered_map,
the unordered_set does not use a ValueType. The set merely stores
elements, and the stored element itself is its own key.
The unordered_set has the same constructors as the unordered_map, but
the set's value_type is equal to its key_type.
When defining an unordered_set type four template arguments must be
specified :
unordered_set::key_type),
unordered_set::hasher), and
unordered_set::key_equal).
The generic definition of an unordered_set container looks like this:
std::unordered_set <KeyType, hash type, predicate type, allocator type>
When KeyType is std::string or a built-in type then default types
are available for the hash type and the predicate type. In practice the
allocator type is not specified, as the default allocator suffices. In these
cases an unordered_set object can be defined by merely specifying the key-
and value types, like this:
std::unordered_set<std::string> rawSet(size_t size = implSize);
Here, implSize is the container's default initial size, which is
specified by the implementor. The set's size is automatically enlarged when
necessary, in which case the container rehashes all its elements. In
practice the default size argument provided by the implementor is
completely satisfactory.
The unordered_set supports the following constructors:
explicit unordered_set(size_type n = implSize,
hasher const &hf = hasher(),key_equal const &eql = key_equal(),allocator_type const &alloc = allocator_type()):
this constructor can also be used as default constructor;
unordered_set(const_iterator begin,
const_iterator end,
size_type n = implSize, hasher const &hf = hasher(),
key_equal const &eql = key_equal(),
allocator_type const &alloc = allocator_type()):
this constructor expects two iterators specifying
a range of unordered_set::value_type const objects, and
unordered_set(initializer_list<value_type> initList,
size_type n = implSize, hasher const &hf = hasher(),
key_equal const &eql = key_equal(),
allocator_type const &alloc = allocator_type()):
a constructor expecting an initializer_list of
unordered_set::value_type values.
The unordered_set does not offer an index operator, and it does not offer
an at member. Other than those, it offers the same members as the
unordered_map. Below the members whose behavior differs from the behavior
of the unordered_map are discussed. For a description of the remaining
members, please refer to section 12.3.12.2.
iterator emplace(Args &&...args):value_type object is constructed from emplace's
arguments. It is added to the set if it is unique, and an iterator to the
value_type is returned.
iterator emplace_hint(const_iterator position,
Args &&...args):value_type object is constructed from the member's
arguments, and if the newly created element is unique it is inserted into the
unordered_set. The
implementation may or may not use position as a hint to start looking
for an insertion point. The returned iterator points to the
value_type.
unordered_set::iterator erase():erase(key_type const &key) erases key from the set. It
returns 1 if the key was removed and 0 if the key wasn't available in
the set.
erase(pos) erases the element pointed to by the iterator
pos. The iterator ++pos is returned.
erase(first, beyond) erases elements indicated by the iterator
range [first, beyond), returning beyond.
unordered_multiset allows multiple objects using the same keys to be
stored in an unordered set. The unordered_multiset container offers the
same set of members and constructors as the unordered_set, but without the
unique-key restriction imposed upon the unordered_set.
Below all members are described whose behavior differs from the behavior of
the corresponding unordered_set members:
size_t count(key_type const &key):value_type object using
key_type key is stored in the unordered_set. This member is
commonly used to verify whether key is available in the
unordered_multiset.
iterator emplace(Args &&...args):value_type object is constructed from emplace's
arguments. The returned iterator points to the newly inserted inserted
value_type.
iterator emplace_hint(const_iterator position,
Args &&...args):value_type object is constructed from the member's
arguments, and the newly created element is inserted into the
unordered_multiset. The
implementation may or may not use position as a hint to start looking
for an insertion point. The returned iterator points to the value_type
using the provided key.
pair<iterator, iterator> equal_range(key):key.
iterator find(key):end is returned.
... insert():
elements may be inserted starting at a certain position. The return value depends on the version ofinsert()that is called. When aniteratoris returned, then it points to the element that was inserted.
iterator insert(value_type const &value)
inserts value.
iterator insert(value_type &&tmp)
inserts value using value_type's move
constructor.
iterator insert(const_iterator hint, value_type const &value)
inserts value, possibly using hint as a
starting point when trying to insert value.
iterator insert(const_iterator hint, value_type &&tmp)
inserts value using value_type's move
constructor, and possibly using hint as a starting point when trying to
insert value.
void insert(first, beyond) inserts the elements in
the iterator range [first, beyond).
void insert(initializer_list <value_type> iniList)
inserts the elements in iniList into the container.
Since the C++14 standard arbitrary lookup key types can be used provided a
comparison operator is available to compare that type with the container's key
type. Thus, a char const * key (or any other type for which an
operator< overload for std::string is available) can be used to lookup
values in a map<std::string, ValueType>. This is called
heterogeneous lookup.
Heterogeneous lookup is allowed when the comparator given to the associative
container does allow this. The standard library classes std::less and
std::greater were augmented to allow heterogeneous lookup.
complex container defines the standard operations that can be
performed on complex numbers. Before using complex containers the
header file <complex> must be included.
The complex number's real and imaginary types are specified as the container's data type. Examples:
complex<double>
complex<int>
complex<float>
Note that the real and imaginary parts of complex numbers have the same datatypes.
When initializing (or assigning) a complex object, the imaginary part may be omitted from the initialization or assignment resulting in its value being 0 (zero). By default, both parts are zero.
Below it is silently assumed that the used complex type is
complex<double>. Given this assumption, complex numbers may be initialized
as follows:
target: A default initialization: real and imaginary parts are 0.
target(1): The real part is 1, imaginary part is 0
target(0, 3.5): The real part is 0, imaginary part is 3.5
target(source): target is initialized with the values of
source.
#include <iostream>
#include <complex>
#include <stack>
using namespace std;
int main()
{
stack<complex<double>>
cstack;
cstack.push(complex<double>(3.14, 2.71));
cstack.push(complex<double>(-3.14, -2.71));
while (cstack.size())
{
cout << cstack.top().real() << ", " <<
cstack.top().imag() << "i" << '\n';
cstack.pop();
}
}
/*
Generated output:
-3.14, -2.71i
3.14, 2.71i
*/
The following member functions and operators are defined for complex
numbers (below, value may be either a primitive scalar type or a
complex object):
complex container.
complex operator+(value):complex container and value.
complex operator-(value):complex container and
value.
complex operator*(value):complex container and
value.
complex operator/(value):complex container and
value.
complex operator+=(value):value to the current complex container, returning the
new value.
complex operator-=(value):value from the current complex container,
returning the new value.
complex operator*=(value):complex container by value, returning
the new value
complex operator/=(value):complex container by value, returning the
new value.
Type real():Type imag():complex container, such as abs, arg, conj, cos,
cosh, exp, log, norm, polar, pow,
sin, sinh and sqrt. All these functions are free functions,
not member functions, accepting complex numbers as their arguments. For
example,
abs(complex<double>(3, -5)); pow(target, complex<int>(2, 3));
istream
objects and inserted into ostream objects. The insertion
results in an ordered pair (x, y), in which x represents the real
part and y the imaginary part of the complex number. The same form may
also be used when extracting a complex number from an istream
object. However, simpler forms are also allowed. E.g., when extracting
1.2345 the imaginary part is set to 0.